Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Equation of Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will discuss the equation of motion for a linear single-degree-of-freedom system. Can someone remind me what an SDOF system is?
It's a system with a single degree of freedom, meaning it can move in one direction only.
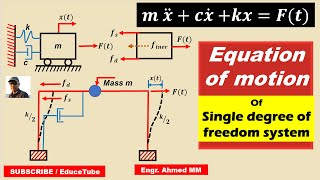
Exactly! Now, the equation of motion for such a system subjected to an external force F(t) is given by: mx¨(t) + cx˙(t) + kx(t) = F(t). Let's break it down. Does anyone know what each term represents?
m is mass, c is damping, k is stiffness, and x(t) is displacement, right?
Perfect! Each term has a crucial role in determining how the system responds to external forces. The left side of the equation represents the system's dynamics, while the right side is the applied force.
Understanding the Terms in the Equation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's dive deeper into the terms: why do you think mass is important in this equation?
It affects the acceleration of the system. More mass means less acceleration for the same force!
Correct! Now, how about the damping coefficient, c?
Damping helps to reduce oscillations and energy in the system over time.
Right again! Damping is vital for controlling vibrations. Lastly, what role does stiffness play?
Stiffness determines how much the system resists deformation.
Exactly! Stiffness affects how quickly the system returns to its equilibrium position after a disturbance.
Applications of the Equation of Motion
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
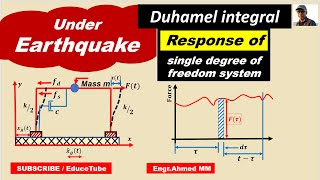
The equation we discussed has real-world implications, especially in earthquake engineering. How do you think it helps engineers?
It helps in predicting how structures behave under seismic loads, right?
Absolutely! By understanding the dynamics described by this equation, engineers can design safer structures. Can anyone think of an example where this might apply?
Buildings in earthquake-prone areas need to be designed to withstand forces from quakes.
Exactly! Using this equation, engineers can determine the required stiffness and damping properties to ensure safe performance during seismic events.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section presents the general equation of motion for a single-degree-of-freedom system, considering mass, damping, and stiffness parameters. It establishes a fundamental framework within structural dynamics, particularly relevant in analyzing the response to arbitrary time-varying forces such as those experienced during earthquakes.
Detailed
Detailed Summary
In this section, we introduce the equation of motion for a linear Single-Degree-Of-Freedom (SDOF) system subjected to a time-varying external force, denoted as F(t). The general equation can be expressed as:
$$ mx¨(t) + cx˙(t) + kx(t) = F(t) $$
where:
- m represents the mass of the system,
- c denotes the damping coefficient,
- k signifies the stiffness of the system,
- x(t) is the displacement of the system over time,
- F(t) is the external force applied.
This equation is a second-order linear differential equation with constant coefficients, fundamental for understanding the motion of the SDOF system under dynamic loading conditions. Analyzing this equation sets the groundwork for further exploration of the Duhamel Integral, which extends the discussion into more complex loading scenarios, particularly in the context of earthquake engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to SDOF Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Consider a single-degree-of-freedom (SDOF) system subjected to an external time-varying force F(t).
Detailed Explanation
In this introductory statement, we are asked to think about a mechanical system that has only one degree of freedom (SDOF). This means it can move in one specific direction or path. Such systems are very common in structural engineering, especially when analyzing how buildings or structures react to various forces. Here, F(t) represents an external force that changes over time, which could be due to things like wind or, in particular contexts such as earthquakes, ground motion.
Examples & Analogies
Imagine a swing hanging from a tree. The swing can move back and forth (only one direction), and if someone pushes it (the external force), the movement of the swing will depend on how hard and fast they push, much like the F(t) in our system.
Equation of Motion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The general equation of motion is given by:
mx¨(t) + cx˙(t) + kx(t) = F(t)
Where:
- m = mass of the system
- c = damping coefficient
- k = stiffness of the system
- x(t) = displacement as a function of time
- F(t) = applied external force
Detailed Explanation
This equation is fundamental in understanding the behavior of SDOF systems. It is a second-order linear differential equation that describes how the mass (m), damping (c), and stiffness (k) interact to determine the displacement (x(t)) of our system in response to an external force (F(t)). The term 'mx¨(t)' represents the inertia (mass times acceleration), 'cx˙(t)' represents damping (resistance to motion), and 'kx(t)' represents the restoring force (the tendency of the system to return to its original position). Together, these components explain how a system responds to forces over time under given conditions.
Examples & Analogies
Consider a car suspension system. The car's mass is analogous to 'm', the suspension's ability to absorb shock is like 'c', and the springs that push the car back up when it compresses relate to 'k'. When the car hits a bump on the road (F(t)), all these factors work together to control how the car moves, helping it to remain stable and providing a comfortable ride.
Nature of the Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This second-order linear differential equation with constant coefficients governs the motion of the system under arbitrary loading.
Detailed Explanation
The phrase 'second-order linear differential equation with constant coefficients' describes the characteristics of the equation governing motion. 'Second-order' means it contains second derivatives (like acceleration), 'linear' indicates that the equation is linear in terms of its terms and solutions, and 'constant coefficients' means that the parameters m, c, and k do not change with time. This type of equation allows us to solve for x(t), the motion over time of the system, under different external conditions, allowing for predictions of behavior under various loads.
Examples & Analogies
Think of a simple pendulum, which can swing back and forth. The motion can be predicted using a similar mathematical approach. If you know how much weight is hanging from the cord (mass), how much the cord stretches (stiffness), and how much the pendulum resists motion (damping), you can anticipate how far and fast it will swing in response to someone giving it a push.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Single-Degree-Of-Freedom (SDOF) System: A system capable of moving in only one direction, modeled with a single coordinate.
-
Mass (m): Reflects the inertia of the system, affecting the response to external forces.
-
Damping (c): Energy dissipation property that causes oscillations to decay over time.
-
Stiffness (k): Measures how resistant a structure is to deformation when subjected to forces.
-
Equation of Motion: A mathematical expression governing the dynamics of the system under external forces.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of an SDOF system is a mass-spring-damper system used to quantify vibrations in a building subjected to wind loads.
-
In earthquake engineering, the equation forms the basis for analyzing structures' responses when subjected to seismic forces.
-
A vehicle suspension system can be modeled as an SDOF system to study how it absorbs shocks from road irregularities.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Mass makes things slow, damping helps them flow, stiffness keeps them tight, together they make motion right.
📖 Fascinating Stories
-
Imagine a swinging pendulum — its mass makes it sway slower, the damping from air keeps it from going forever, while stiffness in the rod keeps it upright!
🧠 Other Memory Gems
-
MDS: Remember Mass, Damping, and Stiffness when thinking about motion response.
🎯 Super Acronyms
MDS - Mass, Damping, Stiffness
- the trio guiding your SDOF understanding.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: SDOF System
Definition:
A single-degree-of-freedom system, which can only move in one direction and is characterized by a single coordinate describing its motion.
-
Term: Mass (m)
Definition:
The quantity of matter in the system, affecting its inertia and response to applied forces.
-
Term: Damping Coefficient (c)
Definition:
A measure of the energy dissipation in the system, reflecting how oscillations decay over time.
-
Term: Stiffness (k)
Definition:
The rigidity of a system that defines how much it deflects under applied loads.
-
Term: Displacement (x(t))
Definition:
The measure of change in position of the system from its equilibrium position over time.
-
Term: External Force (F(t))
Definition:
The time-varying force applied to the system that causes motion.