Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Programming Implementation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will discuss how to implement the Duhamel Integral using programming languages like MATLAB and Python. Who can tell me what the Duhamel Integral is used for?
Isn't it used for analyzing the response of structures to dynamic loads, like earthquakes?
Exactly! Now, why do we need programming for this?
Because the calculations can be very complex and time-consuming if done manually.
Right! Programming allows us to efficiently compute results using numerical methods. Let's dive into the steps needed for implementation.
Steps for Implementation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
The first step is to discretize the time vector. Can someone explain what that means?
It means breaking down continuous time into smaller time intervals, making it easier to perform calculations.
Great! We'll also use known forces or ground acceleration values. Can anyone give an example of one such value?
The data we get from earthquake records, like ground acceleration over time.
Exactly! After we have these values, we calculate the impulse response function at each step. Why do we calculate h(t)?
To understand how the system responds to those forces over time.
Numerical Integration
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's talk about numerical integration. What tools do we use in Python and MATLAB for this?
In Python, we can use `numpy.convolve`, and in MATLAB, we use the `conv` function.
Spot on! These functions help us perform the convolutions needed to compute the integral. Can anyone explain why this step is crucial?
It gives us the total response of the structure based on the past forces applied.
Exactly! Finally, we can generate plots to visualize our results, like time-history plots and displacement responses. Let’s summarize what we learned today.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the implementation of the Duhamel Integral is discussed, focusing on the use of numerical methods in MATLAB and Python. Key procedures include the discretization of time vectors, using known input values, calculating impulse response functions, and applying numerical integration for effective analysis.
Detailed
Programming Implementation (MATLAB/Python)
The Duhamel Integral is an essential computational tool for analyzing the dynamic response of structures under earthquake loads. In this section, we explore how to implement the Duhamel Integral in programming environments such as MATLAB and Python.
Key Implementation Steps:
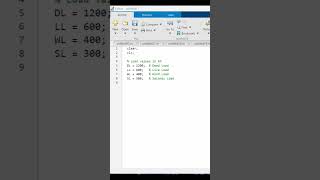
- Discretize the Time Vector: To evaluate the integral numerically, we must define a discrete time vector that breaks the continuous time into manageable increments.
- Utilize Input Values: We’ll use known values for the ground acceleration (u¨g(t)) or external forces (F(t)) throughout our analysis, based on recorded earthquake data.
- Calculate Impulse Response: The impulse response function (h(t)) must be computed at each time step, capturing the system's response characteristics.
- Numerical Integration: Finally, numerical methods such as
numpy.convolvein Python or theconvfunction in MATLAB are utilized to perform the actual integration, yielding important results such as time-history plots, peak displacements, and response spectra.
Through this programming implementation, engineers can simulate real-world scenarios, allowing them to predict the performance of structures to seismic activity.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Discretizing the Time Vector
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The Duhamel integral is often implemented computationally. A typical implementation involves:
- Discretizing the time vector.
Detailed Explanation
Discretizing the time vector means dividing the total time over which we want to compute the system's response into smaller, manageable intervals. This is important because computers cannot handle continuous time signals directly. Instead, we create a list of specific time points (a time vector) at which we will calculate the response of the system. For instance, if we want to analyze the structure's behavior over 10 seconds with intervals of 0.1 seconds, we create a time vector that includes 0, 0.1, 0.2, ..., up to 10.0. Each of these points will be used in calculations.
Examples & Analogies
Think of discretizing the time vector like taking snapshots of a movie. Instead of watching the movie frame-by-frame (continuously), you only look at key moments, say every 10 seconds. This allows you to analyze the movie while keeping the process simple and manageable.
Using Known Ground Acceleration Values
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Using the known u¨ g(t) or F(t) values.
Detailed Explanation
In this context, the term u¨ g(t) refers to the ground acceleration data, which is essential input for the Duhamel integral. This data can come from real earthquake recordings as measured by seismographs. By knowing the ground motion (acceleration), we can effectively apply it to analyze how the structure reacts to that motion. This step is crucial because the actual forces or accelerations acting on the structure during an earthquake need to be understood accurately for the calculations to be meaningful.
Examples & Analogies
Imagine you're trying to determine how a boat reacts to waves. You wouldn't just guess the size of the waves; instead, you would measure the waves and use this data (wave height and frequency) to understand how the boat behaves. Similarly, by using actual acceleration values from earthquakes, we can see how buildings respond during real events.
Calculating Impulse Response at Time Steps
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Calculating h(t) at each time step.
Detailed Explanation
The impulse response function, h(t), describes how the system reacts over time to a unit impulse (a sudden force). In our computational implementation, at each time step we've defined in our vector, we calculate the corresponding impulse response. This reflects how the system's reaction changes based on varying conditions over time. For example, if we are calculating it at t=0.1 seconds, we determine how a unit force impacts the structure at that exact moment, providing insight into the system's ongoing behavior.
Examples & Analogies
Imagine you're adjusting a dial on a stereo system to increase the volume. At each small turn of the dial, you don't just flip the switch; you are gradually changing how the sound fills the room. Similarly, calculating h(t) at each time step provides a detailed view of how the structural response builds up over each increment, just like the sound changes with each adjustment.
Applying Numerical Integration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Applying numerical integration (e.g., numpy.convolve in Python or conv in MATLAB).
Detailed Explanation
Numerical integration is a mathematical technique used to approximate the value of an integral, especially when dealing with complex functions that cannot be integrated analytically. In this case, we use numerical methods to approximate the convolution of the impulse response function and the ground acceleration values over our time vector. Functions like numpy.convolve in Python or conv in MATLAB provide efficient ways to perform this operation, yielding the structure's response effectively. This is akin to summing over these contributions to yield a final result.
Examples & Analogies
Think about baking a cake where you need to mix different ingredients. Instead of just throwing everything in at once, you mix them gradually and systematically to achieve the perfect batter. Applying numerical integration is similar; it helps systematically combine our impulse responses with the forces over time to get a complete picture of how the structure will respond.
Generating Time-History Plots and Spectra
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
- Sample code is often written to generate time-history plots, peak displacement, and response spectra.
Detailed Explanation
After we have computed the system's response using the Duhamel integral, we can visualize it through time-history plots, which show how the displacement changes over time. This helps engineers understand how the structure behaves during an earthquake. Additionally, we generate response spectra, which provide vital information about the maximum expected responses over a range of frequencies. These visualizations are critical for assessing building safety and designing future structures.
Examples & Analogies
Consider an athlete keeping track of their training progress. They create charts and graphs to see how their running times improve over the weeks. Similarly, time-history plots and response spectra help engineers visualize and understand the data derived from their calculations, making it easier to analyze the effects of earthquakes on structures.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Discrete Time Vector: A representation of time in small increments for computational analysis.
-
Impulse Response Function: A vital mathematical function representing the system's output in response to an impulse.
-
Numerical Integration: Techniques that allow us to approximate the result of an integral easily.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of how ground acceleration data is used to calculate structural response using Duhamel Integral.
-
A simulation of earthquake effects on structures generated using Python to visualize displacement over time.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In response to loads, we calculate right, with Duhamel's Integral, it's out of sight!
📖 Fascinating Stories
-
Imagine a bridge in a storm; the Duhamel Integral helps us see how much it sways and transforms!
🧠 Other Memory Gems
-
For Duhamel, Remember: Divide, Use data, Integrate, and Visualize (D.U.I.V.)!
🎯 Super Acronyms
D.I.V.E. - Discretize, Input data, Verify results, Evaluate response.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Duhamel Integral
Definition:
A mathematical formulation used to express the response of a system to arbitrary dynamic loading.
-
Term: Impulse Response Function
Definition:
The system response to a unit impulse force applied at time zero, essential for analyzing the system's behavior.
-
Term: Discretization
Definition:
The process of dividing a continuous signal or time domain into discrete parts.
-
Term: Numerical Integration
Definition:
A mathematical technique used to evaluate integrals numerically, often required in computing responses in engineering.