Frequency Ratios and Modal Participation
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Frequency Ratios
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to discuss frequency ratios, which are crucial in earthquake engineering. Can anyone tell me what a frequency ratio is?

Is it the ratio of different frequencies?

Exactly! The frequency ratio is the comparison between the forcing frequency from ground excitation and the structure's natural frequency. Can someone describe what happens when this ratio approaches one?

I think that's when we experience resonance!

Correct! Resonance can amplify vibrations and potentially lead to structural failure. Just remember, *frequency meets frequency at one, but beware, resonance isn’t fun!*
Understanding Modal Participation Factor
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s delve into modal participation factors. Why do you think knowing how much each mode contributes to overall response is vital?

It helps us understand which parts of the structure are most affected during an earthquake?

Exactly! The modal participation factor tells us how much a particular mode influences the total structural response. It's essential for designing resilient buildings. Can anyone recall how we utilize this in analysis?

In response spectrum analysis and using modal superposition?

That's spot on! Remember, understanding these factors can save lives and properties. *Modal matters in design; understand and intertwine!*
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
Frequency ratios are defined as the relationship between ground excitation frequency and a structure's natural frequency. Modal participation factors provide insight into the contribution of individual mode shapes to total structural response, which is essential for accurate seismic design and analysis.
Detailed
Frequency Ratios and Modal Participation
In earthquake engineering, understanding the frequency ratios and modal participation is essential for effective structural analysis and response prediction. This section elaborates on two key concepts:
Frequency Ratio
The frequency ratio () is the ratio of the forcing frequency () caused by ground excitation to the structure's natural frequency ()n. Mathematically, it can be expressed as:
= /
Resonance phenomena occur when the frequency ratio approaches unity ( 1). This condition can intensify vibrations, posing a risk for structural integrity during seismic events.
Modal Participation Factor
The modal participation factor quantifies how much a specific mode contributes to the overall response of the structure. This is particularly important in response spectrum analysis and when employing modal superposition. Understanding these factors helps engineers design buildings that can withstand dynamic excitations by appropriately accounting for the contributions of different mode shapes during an event.
In conclusion, the correct analysis of frequency ratios and modal participation is vital for ensuring structures can effectively respond to seismic forces, enhancing their resilience against earthquakes.
Youtube Videos
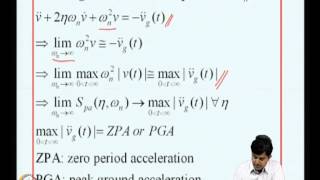









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Frequency Ratio Explained
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Frequency Ratio
- Ratio between the frequency of ground excitation and the structure’s natural frequency:
\( r = \frac{\omega}{\omega_n} \)
- Where:
- \( \omega \): forcing frequency
- \( \omega_n \): natural frequency
- Resonance occurs when \( r \approx 1. \)
Detailed Explanation
The frequency ratio is a crucial concept in understanding the interaction between a structure and external forces, like those from an earthquake. It compares the frequency of external forces (forcing frequency, \( \omega \)) to the natural frequency of the structure (\( \omega_n \)). When the ratio \( r \) approaches 1, it indicates that the external forces are aligned with the natural frequency of the structure. This alignment can lead to resonance, amplifying the vibrations and potentially causing significant damage to the structure.
Examples & Analogies
Imagine pushing someone on a swing. If you push them at just the right moment (matching their natural frequency), the swing will go higher and higher—that’s resonance. If you push them out of sync, they won't gain much height. Similarly, in buildings, if an earthquake's frequency matches the building's natural frequency, it can lead to dangerous vibrations.
Understanding Modal Participation Factor
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Modal Participation Factor
- Measures how much a particular mode contributes to total structural response.
- Important in response spectrum analysis and mode superposition method.
Detailed Explanation
The modal participation factor is a numerical value that helps engineers understand how much each mode of vibration in a structure contributes to its overall response during an event like an earthquake. Different modes can behave differently under load, and some modes might contribute more significantly to the structure's response than others. This factor plays a vital role in response spectrum analysis and the mode superposition method, which are techniques used to predict how the structure will behave during seismic events.
Examples & Analogies
Think of a choir performing. Each singer represents a different mode of the structure. Some singers might have a strong voice that stands out, contributing more to the overall harmony (like a dominant mode contributing more to structural response), while others have softer voices that add background harmony but are less noticeable. The modal participation factor helps identify which 'singers' are most important during an earthquake.
Key Concepts
-
Frequency Ratio: The ratio of ground excitation frequency to natural frequency that indicates resonance.
-
Modal Participation Factor: Describes the contribution of a mode to a structure's overall response.
Examples & Applications
If a building's natural frequency is 1 Hz and it experiences ground shaking at 1 Hz, it could lead to resonance and potential failure.
In a building with multiple modes, assessing the modal participation factors helps engineers understand which modes dominate during seismic events.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When frequency meets frequency, it's fine; but if they align, it may not be divine.
Stories
Imagine a musician tuning their guitar to match the note of a piano; when they hit the same note, the sound resonates beautifully. However, if they were out of tune, the harmony would turn into a chaotic noise, just like how buildings can face risks during earthquakes.
Memory Tools
FIRM: Frequency, Impact, Resonance, Modes - remember how each factor relates in building design.
Acronyms
FIRM
Frequency Ratio
Impact of Modes
Reliability in design - a guide to understanding critical concepts.
Flash Cards
Glossary
- Frequency Ratio
The ratio between the frequency of ground excitation and the structure’s natural frequency.
- Modal Participation Factor
A measurement of how much a particular mode contributes to the total structural response.
Reference links
Supplementary resources to enhance your learning experience.
