Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Rayleigh's Method
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's start by discussing Rayleigh's Method for calculating the natural frequencies of structures. Does anyone know why we would use an approximate method like this?
Maybe because it's simpler than trying to calculate everything exactly?
Exactly! Rayleigh’s method simplifies calculations by using assumed mode shapes. It relies on energy principles to estimate frequencies. Remember the formula ω² = E I (d²y/dx²) / ρ A y dx? Can anyone tell me what each term stands for?
E is Young's modulus, right? And ρ is density?
Great! That’s correct. E represents stiffness properties, while ρ refers to the mass density. Understanding these terms helps grasp how we calculate natural frequencies using Rayleigh’s method.
How does choosing different mode shapes affect the results?
Good question! The choice of mode shapes can influence the accuracy of the method. It's essential to select reasonable shapes that represent the actual behavior of the structure. This balance between accuracy and simplicity is key in engineering design.
Understanding Finite Element Method (FEM)
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Moving on to the Finite Element Method, often referred to as FEM. Can anyone explain what FEM entails in the context of frequency calculation?
It breaks down complex structures into smaller elements to make calculations easier?
Exactly! This approach allows for a numerical solution to the eigenvalue problem, which is necessary for finding natural frequencies and mode shapes of structures. Why is this method particularly useful in earthquake engineering?
Because buildings can be really complex and need accurate modeling?
Yes, precisely! MDOF systems can exhibit intricate behaviors that analytical methods might not fully capture. FEM is widely used because it accommodates varying mass distribution, stiffness, and boundary conditions.
How do engineers ensure that the elements are accurately sized?
A good point! Engineers perform convergence studies to refine the mesh, ensuring that results improve with smaller elements. Balancing computational resources and accuracy is crucial in FEM.
Application of Numerical Methods in Design
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we have covered the methods, let’s discuss their practical applications in structural design. How do Rayleigh’s Method and FEM contribute to designing earthquake-resistant structures?
They help engineers understand how a structure will respond to seismic events, so they can make it safer.
Exactly! Knowing the natural frequency allows engineers to avoid resonance, which can lead to catastrophic failures. Can anyone think of a scenario where a design could fail because of poor frequency matching?
Like buildings collapsing during an earthquake if their frequency matches that of the seismic waves?
Correct! Designing with an awareness of natural frequencies is essential for safety, particularly in earthquake-prone areas. The combination of analytical and numerical methods provides a comprehensive approach to structural resilience.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, two numerical methods for frequency calculation are elaborated: Rayleigh’s Method, which approximates natural frequencies using assumed mode shapes, and the Finite Element Method (FEM), which numerically solves the eigenvalue problem for complex structures by discretizing them into smaller elements. Both methods are critical in the analysis and design of structures for earthquake resilience.
Detailed
Numerical Methods for Frequency Calculation
This section explores important numerical methods used to calculate the natural frequencies of structures, focusing primarily on Rayleigh's Method and the Finite Element Method (FEM).
Rayleigh’s Method
Rayleigh’s Method provides an approximate technique for determining the natural frequencies of systems by using assumed mode shapes. It is based on the principle of energy conservation, leading to a simplified calculation of vibration characteristics. The formula employed in Rayleigh's method is:
Where each symbol represents physical quantities associated with the structure, reflecting the interplay of stiffness, mass distribution, and deformation.
Finite Element Method (FEM)
The Finite Element Method is a widely utilized numerical technique for calculating natural frequencies and mode shapes in more complex structures. FEM works by discretizing a structure into smaller, manageable finite elements, allowing for a numerical solution to the eigenvalue problem. This approach is particularly effective in analyzing multi-degree-of-freedom (MDOF) systems where analytical solutions may be impractical.
FEM enables engineers to accurately compute how structures respond under dynamic conditions, essential for earthquake-resistant design.
By leveraging these numerical methods, engineers can predict resonance phenomena and optimize structural designs for safety and performance.
Youtube Videos
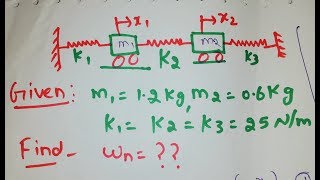
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Rayleigh’s Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
An approximate technique using assumed mode shapes:
$$RL EI \left( \frac{d^2y}{dx^2} \right)^2 \omega^2 = 0 \quad RL \int_0^L \rho A y^2 dx$$
Detailed Explanation
Rayleigh's Method is a technique used to estimate the natural frequencies of a structure by assuming certain mode shapes. It involves a mathematical approach where the stiffness and mass characteristics of the structure are analyzed. The first part of the equation relates to the potential energy of the system due to the stiffness, representing how much energy can be stored in the material during deformation. The second part integrates the mass distribution over the length of the structure, which accounts for how the total mass influences vibrations. This method allows engineers to find approximate natural frequencies without needing to solve complex equations completely.
Examples & Analogies
Imagine a child on a swing. When the child swings back and forth, they naturally oscillate at a certain rhythm or frequency. If we think of the swing as a system, Rayleigh’s Method helps us estimate how fast the swing (our structure) can go back and forth depending on how stiff the swing set is and how much the child weighs.
Finite Element Method (FEM)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• FEM is widely used in practice to compute natural frequencies and mode shapes.
• Discretizes the structure into elements and solves the eigenvalue problem numerically.
Detailed Explanation
The Finite Element Method (FEM) is an advanced computational technique employed to calculate natural frequencies and mode shapes of complex structures. It works by breaking down the entire structure into smaller, manageable pieces called finite elements. Each element can be analyzed individually, and then the results are compiled to give an overall view of the entire structure's behavior. This method is particularly useful because it allows engineers to consider various material properties and geometric configurations, providing more accurate frequency calculations compared to simpler methods.
Examples & Analogies
Think of FEM like assembling a jigsaw puzzle. Instead of trying to visualize the whole picture at once (which can be overwhelming), you focus on solving one smaller piece at a time. Once all the individual pieces are solved, they come together to reveal the entire image, just as FEM combines results from many small elements to understand the whole structure's vibrational characteristics.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Rayleigh's Method: An approximation technique for frequency calculation based on assumed mode shapes.
-
Finite Element Method (FEM): A numerical approach that divides structures into elements for solving dynamic problems like frequency calculation.
-
Mode Shape: A characteristic shape exhibited by a structure at a specific natural frequency.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of using Rayleigh's Method is in calculating the fundamental frequency of a cantilever beam by assuming a specific deflected shape.
-
In FEM, engineers might analyze a complex multi-storey building to determine its modal response to seismic loading by applying the method to each finite element.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When calculating frequency's thrill, Rayleigh's Method can fit the bill!
📖 Fascinating Stories
-
Imagine a bridge that shakes during an earthquake. Rayleigh and FEM are like wise engineers working together to find the right way to help it withstand the force and keep people safe.
🧠 Other Memory Gems
-
Remember Rayleigh's Method's Focus (RMF) on approximations and simplified structures.
🎯 Super Acronyms
FEM - **F**inite - **E**lements - **M**odeling for dynamic analysis.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Rayleigh’s Method
Definition:
An approximate technique for calculating natural frequencies using assumed mode shapes.
-
Term: Finite Element Method (FEM)
Definition:
A numerical method that discretizes a structure into smaller elements to solve the eigenvalue problem for natural frequency calculations.
-
Term: Eigenvalue Problem
Definition:
A mathematical problem in which one seeks the values (eigenvalues) and corresponding shapes (eigenvectors) relevant to natural frequencies of a structure.
-
Term: Mode Shape
Definition:
The shape that a structure assumes at its natural frequency.
-
Term: Discretization
Definition:
The process of splitting a continuous domain into smaller, manageable pieces for analysis.