Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to MDOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're diving into Multi-Degree of Freedom systems, or MDOF. These systems are crucial because structures like buildings have multiple natural frequencies due to their many degrees of freedom.
Why do buildings have multiple natural frequencies?
Great question! Buildings can vibrate in various ways—think of them as having many distinct shapes or modes they can assume when disturbed. That's why we analyze these frequencies.
How do we find these natural frequencies?
Naturally! We use something called an eigenvalue problem, which involves matrices. We'll get into that in detail, but remember: more degrees of freedom mean more ways to vibrate!
Understanding Eigenvalue Problems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
To find the natural frequencies of our MDOF systems, we set up an equation called the eigenvalue problem: [K − ω²M]φ = 0. Can anyone tell me what K and M refer to?
K is the stiffness matrix, and M is the mass matrix, right?
Exactly! And when we solve this, we will have multiple eigenvalues, which correspond to different frequencies.
And what about the mode shapes?
Excellent! The corresponding eigenvectors give us the mode shapes—how the structure vibrates at each frequency!
Significance of MDOF in Structural Engineering
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, why is understanding MDOF systems particularly important for earthquake engineering?
Because buildings need to resist seismic vibrations, right?
Exactly! By knowing the natural frequencies and mode shapes, we can design buildings that can safely withstand seismic forces.
And we can analyze their response using modal analysis, right?
Yes! Modal analysis helps us consider each mode's contribution to the overall response, which is essential for ensuring safety.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
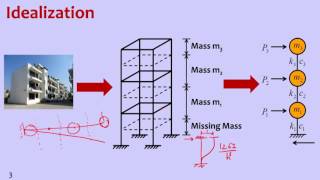
In MDOF systems, structures like multi-storey buildings have several natural frequencies due to their complex behavior under dynamic loads. Understanding the eigenvalue problem allows for determining these frequencies and corresponding mode shapes, which are crucial for evaluating and designing earthquake-resistant structures.
Detailed
Multi-Degree of Freedom Systems (MDOF)
MDOF systems are characterized by multiple degrees of freedom, fundamentally affecting how structures respond to dynamic forces, particularly in earthquake engineering. Each MDOF structure possesses various natural frequencies that arise from its complex geometry and construction.
Eigenvalue Problem
To determine the natural frequencies of an MDOF system, we solve the eigenvalue problem defined as:
[K − ω²M]φ = 0
where:
- K is the stiffness matrix
- M is the mass matrix
- φ is the mode shape
- ω is the natural frequency
Solving this mathematical framework produces multiple eigenvalues (representing different frequencies) and associated eigenvectors (representing mode shapes).
Understanding these frequencies and modes is crucial for efficiently designing structures to withstand earthquakes. By utilizing concepts such as modal analysis and the principle of modal superposition, engineers can predict how the MDOF structure will behave under dynamic loads, ensuring safety and resilience.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to MDOF Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Structures like multi-storey buildings have more than one natural frequency due to their multiple degrees of freedom.
Detailed Explanation
Multi-Degree of Freedom (MDOF) systems refer to structures that can vibrate in more than one direction or mode. Unlike Single Degree of Freedom (SDOF) systems, which have a single frequency and movement path, MDOF systems can vibrate at multiple frequencies simultaneously. For example, a multi-storey building can sway, twist, or bend in various ways depending on how forces are applied to it. Each mode of vibration corresponds to different natural frequencies.
Examples & Analogies
Consider a trampoline: when you jump on it, the entire surface bounces up and down (like the SDOF system), but as more people jump and move around, various parts of the trampoline react differently, creating different vibrations throughout the surface (akin to MDOF). This phenomenon is especially important for tall buildings that can sway during earthquakes.
Eigenvalue Problem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
To find the natural frequencies:
[K−ω²M]ϕ=0
Where:
• K = stiffness matrix
• M = mass matrix
• ϕ = mode shape
• ω = natural frequency
Solving this gives multiple eigenvalues (frequencies) and eigenvectors (mode shapes).
Detailed Explanation
The equation provided is crucial for determining the natural frequencies of an MDOF system. Here, K represents the stiffness of the structure, M is the mass distribution, ω is the natural frequency we are trying to find, and ϕ denotes the mode shape, or how different parts of the structure move during a particular mode of vibration. This is known as the eigenvalue problem in structural dynamics. When solving it, we derive multiples of natural frequencies (eigenvalues) and associated mode shapes (eigenvectors). Understanding these helps engineers predict how structures will react under dynamic loading.
Examples & Analogies
Imagine a group of musicians playing different instruments. Each musician's performance can be seen as a mode shape, while the overall harmony is akin to the natural frequencies. When you change an instrument or its position in the band (changing stiffness or mass), the overall sound changes too. This is similar to how adjusting the parameters in the equation will alter the natural frequencies and vibrations of the structure.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Multiple Degrees of Freedom: Structures have several ways to vibrate.
-
Eigenvalue Problem: The mathematical approach to find natural frequencies and mode shapes.
-
Stiffness and Mass Matrices: Key matrices used in the analysis of MDOF systems.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A multi-storey building responding to seismic loads with different vibrational modes.
-
Vibration analysis of a bridge using FEM to determine natural frequencies.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In MDOF's dance, structures sway, with frequencies that hold the sway.
📖 Fascinating Stories
-
Imagine a tree in the wind, bending in various ways. Just like a tree has many ways to sway, so do structures with multiple degrees of freedom.
🧠 Other Memory Gems
-
Remember 'K M F' for the core concepts: K for Stiffness, M for Mass, F for Frequencies.
🎯 Super Acronyms
Use 'MOD' to recall
- M: for Multi
- O: for Oscillation
- D: for Degrees of Freedom.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: MDOF (MultiDegree of Freedom)
Definition:
A structural system with multiple degrees of freedom, leading to multiple natural frequencies.
-
Term: Eigenvalue Problem
Definition:
A mathematical formulation to determine the natural frequencies and mode shapes of a system.
-
Term: Stiffness Matrix (K)
Definition:
A matrix that quantifies the stiffness properties of a structure in terms of forces and displacements.
-
Term: Mass Matrix (M)
Definition:
A matrix that quantifies the mass properties of a structure.
-
Term: Mode Shape (φ)
Definition:
The shape a structure assumes when vibrating at a particular natural frequency.