Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Reduces Computational Effort
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
The Mode Superposition Method greatly reduces the computational effort involved in analyzing structures under dynamic forces. By breaking down a complex MDOF system into simpler SDOF systems, we can solve them more efficiently.
How exactly does it reduce that effort?
Think of it like splitting a large puzzle into smaller sections. Each piece can be managed more easily, leading to a quicker overall assembly. The uncoupling of equations makes it much less taxing on computational resources.
So it sounds like we can focus on each mode individually without losing the whole system's behavior?
Exactly! Each modal response represents how a system would behave in isolation, and when we superimpose these, we get the entire responsive picture.
Would that mean faster results?
Yes, speeding up design processes significantly! Let’s remember: faster computation allows for more iterations and better designs.
Insight into Dynamic Behavior
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Another key advantage is the insight this method provides into dynamic behavior. Each mode's contribution is clear and helps engineers understand the impact of different dynamic factors.
Why is understanding each mode’s contribution important?
Knowing how each mode contributes allows us to identify vulnerabilities in a structure. For instance, if a specific mode resonates with external forces like earthquakes, we know where to focus our reinforcement efforts.
Can this method indicate which modes are not significant?
Absolutely! Engineers can often ignore higher modes that contribute minimally, which streamlines the analysis further.
What would happen if we disregard significant modes?
Ignoring significant modes can lead to safety risks. Always best to analyze until you achieve an adequate understanding.
Application in Modern Software
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
The Mode Superposition Method is widely utilized in modern structural engineering software like SAP2000, ETABS, and STAAD Pro. This application shows its relevance in practice.
What benefits does this provide for engineers working with software?
These programs simplify complex analyses and eliminate the need to derive the equations manually, allowing engineers to focus on design and safety. Just input the data and let the software do the heavy lifting.
Can it be used for both seismic and other dynamic analyses?
Yes! It's effective for both time history and response spectrum analyses, making it quite versatile.
Are there situations where this method might not be applicable?
Yes, it's essential to recognize its limitations, especially with highly nonlinear systems, but overall, it's a key tool in structural dynamics.
Efficiency for Linear Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
The Method is particularly efficient for linear systems, as it leverages the properties of linearity to simplify calculations.
What makes linear systems different in this context?
In linear systems, superposition principles hold, allowing us to combine responses directly. Nonlinear systems behave unpredictably, complicating analyses.
Is that why we see it used so often in practice?
Precisely! The predictability of linear systems alongside the computational efficiency makes it a go-to method for many engineering assessments.
So we can always trust the output from tools that use this method?
While it’s a reliable method for linear problems, understanding context and conditions remains critical for accuracy in all analysis.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The advantages of the Mode Superposition Method include reducing computational complexity by transforming multi-degree-of-freedom equations into simpler single-degree-of-freedom systems, enhancing insights into modal contributions, and being applicable in both seismic analysis and design. This method is vital in structural engineering software for effective analysis.
Detailed
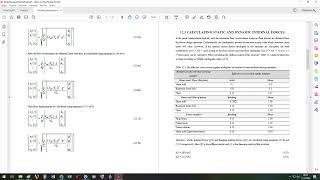
The Mode Superposition Method is an essential tool in structural dynamics, particularly in the evaluation of structures subjected to dynamic loading, such as seismic events. By enabling the analysis of multi-degree-of-freedom (MDOF) systems through a simplification to single-degree-of-freedom (SDOF) systems, it allows engineers to leverage the decoupling of complicated equations into manageable individual modal responses. The advantages include substantial reductions in computational effort, provision of detailed insights into dynamic behavior via individual modal contributions, and its solid integration into modern structural engineering software like SAP2000, ETABS, and STAAD Pro. It is applicable for both time history analysis and response spectrum analysis, making it a versatile method for engineers.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Computational Efficiency
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Reduces computational effort by solving uncoupled SDOF systems.
Detailed Explanation
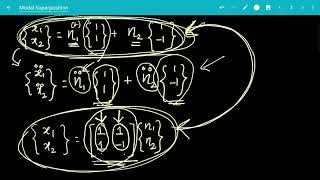
The Mode Superposition Method greatly simplifies the process of analyzing a multi-degree-of-freedom (MDOF) system by breaking it down into single-degree-of-freedom (SDOF) systems. This means instead of solving a complex set of interrelated equations that describe the behavior of the entire structure, the method focuses on simpler equations that are independent of each other for each mode of vibration. By doing this, the computational effort required is significantly reduced, leading to faster analysis and results.
Examples & Analogies
Think of this method like managing a large team project by breaking it into smaller tasks assigned to different team members. Instead of juggling all aspects of the project at once, each member focuses on their task independently. This approach not only makes things easier to manage but also speeds up overall progress.
Insight into Dynamic Behavior
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Insight into dynamic behavior through individual modal contributions.
Detailed Explanation
One of the key advantages of the Mode Superposition Method is the ability to analyze and understand how each mode contributes to the overall dynamic behavior of the structure. By examining individual modes, engineers can gain insight into which modes have the most significant impact on the structure's response to dynamic loading, such as during an earthquake. This knowledge allows for targeted design improvements and better risk assessments for potential vulnerabilities.
Examples & Analogies
Imagine a symphony orchestra, where each musician plays a different instrument. To understand the overall sound of the orchestra, one might listen to individual instruments separately. This helps identify which instruments are contributing most to the music. Similarly, in engineering, analyzing each vibration mode helps identify the most influential factors affecting a structure's safety and performance during dynamic events.
Software Application
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Efficient for linear systems and widely used in software like SAP2000, ETABS, and STAAD Pro.
Detailed Explanation
The Mode Superposition Method is particularly effective for analyzing linear systems. This means it is well suited for many types of civil engineering structures, including buildings and bridges. Popular structural analysis software, such as SAP2000, ETABS, and STAAD Pro, have integrated this method because it allows for efficient and accurate dynamic analysis. By utilizing the method, these tools can quickly compute responses from seismic forces and other dynamic loads.
Examples & Analogies
It's like using a specialized application on your smartphone that quickly and efficiently organizes your personal schedules or finances. Just as you rely on software to streamline your life, engineers use advanced tools that employ the Mode Superposition Method to make complex calculations quicker and easier. This allows them to focus on design solutions instead of getting bogged down in tedious calculations.
Versatility in Analysis Types
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Applicable for both time history and response spectrum analyses.
Detailed Explanation
The versatility of the Mode Superposition Method is another advantage. It can be applied to different analysis types, including time history analysis, which looks at how structures respond over time to motion (like earthquakes), and response spectrum analysis, which evaluates the maximum expected response of a structure given a set of seismic input parameters. This flexibility allows engineers to use the same method for various scenarios in structural dynamics, enhancing the method's utility.
Examples & Analogies
Think of the Mode Superposition Method as a versatile tool in a toolbox that can be used for multiple tasks. Just like a Swiss Army knife can serve various functions—like cutting, screwing, or opening bottles—this method can tackle different types of dynamic analysis, making it a valuable resource for engineers addressing a wide range of challenges in structural design.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Computational Efficiency: The Mode Superposition Method reduces computational effort by uncoupling MDOF systems into simpler SDOF systems.
-
Modal Contributions: The method provides insights into the specific contributions of each mode, which aids in design and safety assessments.
-
Software Integration: Widely used in modern structural engineering software, facilitating quicker and more efficient analyses.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An engineer using the Mode Superposition Method to analyze the seismic response of a high-rise building during an earthquake simulation.
-
Utilizing SAP2000 to perform a dynamic analysis, engineers can quickly assess how different modes influence the overall structural behavior.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Mode superposition is so grand, breaks down dynamics with a steady hand.
📖 Fascinating Stories
-
Imagine a group of engineers tackling a giant puzzle. They quickly realize that if they focus on small sections first, the overall picture becomes clearer, showing how each piece fits together securely.
🧠 Other Memory Gems
-
RICE: Reduces computational effort, Insight into dynamics, Computation efficiency, Easily integrated.
🎯 Super Acronyms
MPS
- Mode Power Solution for analyzing natural responses.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mode Superposition Method
Definition:
An analytical technique for simplifying the analysis of structures subjected to dynamic loads by decomposing their response into a combination of individual modal responses.
-
Term: SingleDegreeofFreedom (SDOF)
Definition:
A simplified model of a system that can be described by a single displacement coordinate.
-
Term: MultiDegreeofFreedom (MDOF)
Definition:
A structural system with multiple interconnected elements that can move independently, leading to complex response behaviors.
-
Term: Modal Analysis
Definition:
A process to determine the natural frequencies and mode shapes of a structure which characterize its behavior under dynamic loading.