18.15. Mode Localization and Coupled Modes

In irregular or asymmetric structures, certain modes may not be global:

• Localized Modes: Vibrations confined to specific portions of the structure (e.g., stairs, cantilevered sections).

Localized modes refer to vibrations that are not uniformly spread throughout the entire structure. Instead, they are concentrated in specific areas, such as stairs or cantilever sections. This occurs in irregular or asymmetric structures where the distribution of mass and stiffness is not consistent. For example, if a building has a stairwell that is significantly stiffer than the rest of the structure, the vibrations produced during an earthquake may be more pronounced in that area, leading to a localized mode of vibration.

Imagine a guitar string being plucked. While the string vibrates as a whole, if you press down on one section of the string (like the stairs in our building example), you may notice that the vibrations are more pronounced around that section, creating a local sound that is different from the overall sound of the string. This is akin to the localized modes where specific parts of the structure react differently under stress.

• Coupled Modes: Translational and rotational modes occurring simultaneously due to eccentricity or plan irregularity.

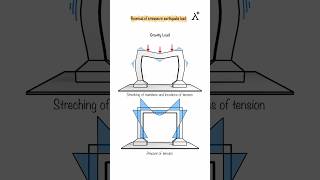
Coupled modes occur when translational (up and down or side to side) and rotational motion (twisting) happen at the same time. This situation arises due to structural characteristics such as eccentricity (when the mass center and stiffness center do not align) and irregularities in plan geometry. For instance, if a building has an asymmetrical layout, the vibrations during an earthquake might create both lateral movement of the floors and twisting simultaneously, leading to a coupled mode of vibration.

Think of a seesaw with a friend sitting off-center. When you jump on one side, not only does that side go up and the other side go down (translational movement), but the seesaw might also tilt slightly as it goes up. This off-center movement represents coupled modes: both translation and rotation occurring together, just like how certain irregular structures might behave during dynamic loads.

These conditions may require:

• Advanced modeling techniques
• Mass eccentricity considerations
• Inclusion of accidental torsion

When dealing with localized and coupled modes, engineers must use advanced modeling techniques to accurately capture the complex behavior of these irregular structures. This includes accounting for mass eccentricity, which is the difference between the center of mass and the center of stiffness, often requiring more sophisticated analysis methods. Accidental torsion, or the unintentional twisting of a structure during loading, must also be included in the model to ensure safety and performance during an event such as an earthquake.

Imagine trying to balance a seesaw again, but this time with weights placed at irregular intervals. To properly model how the seesaw would move with people on it, you’d need to consider where those weights are located and how they affect the balance. Similarly, structural engineers must think about where mass is distributed in irregular buildings and use specific methods to create models that accurately reflect the potential movements of the building in response to forces.

--