Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Seismic Loading Input
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we will discuss how seismic loading affects structures. Can anyone tell me what ground acceleration represents in this context?
Is it the force that the ground exerts during an earthquake?
Exactly! Ground acceleration, denoted as `u¨g(t)`, is the input we use in our analyses. It serves as the external force acting on the structure during seismic events.
So, how does this affect the structure's response?
Great question! The structure responds by vibrating in various modes. We apply the Mode Superposition Method to analyze this more effectively.
What are modal responses?
Modal responses are the individual contributions from each vibration mode of a structure due to the applied ground acceleration. Let’s summarize: Ground acceleration is a key input for seismic analysis, leading to individual modal responses.
Superposition of Modal Responses
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's discuss how we obtain the total structural response from individual modal equations. Who can explain this process?
We sum the responses from each mode?
Correct! We superimpose the individual modal responses to find the total response. This method allows us to manage the complexity of MDOF systems.
Is there a limit to how many modes we include?
Yes, typically we consider the first 3 to 5 modes, which often capture most of the seismic behavior, especially for lower structures. Let's recap: We calculate the total response by summing the modal responses, focusing on the most significant 3 to 5 modes.
Importance of Mode Superposition
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
What advantages do you think the Mode Superposition Method offers for seismic analysis?
It simplifies the calculations by breaking them down into smaller parts?
Exactly! By solving each mode separately, we reduce computational effort significantly. Additionally, it offers valuable insights into the dynamic behavior of a structure.
Are there situations where we might miss higher mode contributions?
Yes! Taller buildings or those that are more flexible may require consideration of higher modes. Always ensure that you analyze the contributions correctly!
To summarize, the Mode Superposition Method is effective for simplifying seismic analysis and gaining crucial insights!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The Mode Superposition Method is essential for analyzing structures under seismic loading. It involves solving individual modal equations for each mode based on ground acceleration input, allowing for efficient determination of total structural response through superposition of modal responses.
Detailed
Application to Seismic Analysis
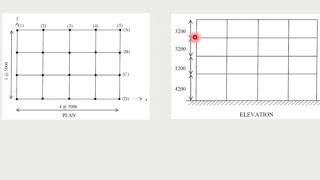
In seismic analysis, it is crucial to assess how a structure responds to ground motion during an earthquake. The Mode Superposition Method offers a systematic approach to simplify this assessment by breaking down the complex response of multi-degree-of-freedom (MDOF) systems into simpler components.
- Ground Acceleration: The external force acting on the structure is represented by ground acceleration, denoted as
u¨g(t). - Modal Responses: Each modal equation is individually solved for
q_i(t)concerning this acceleration, leading to distinct responses from each mode. - Superposition of Modal Responses: The total structural response is obtained by superimposing these individual modal responses.
Key Considerations:
- Typically, only the first 3 to 5 modes capture most of the seismic impact. Higher modes may be significant for taller structures or those with greater flexibility.
This method effectively allows engineers to ensure the safety and stability of structures during seismic events by accurately assessing both low-rise and high-rise constructions.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Ground Acceleration as External Input
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When analyzing a structure for seismic loading:
- The ground acceleration u¨ g(t) is input as an external force.
Detailed Explanation
In the context of seismic analysis, the ground motion during an earthquake can be represented mathematically as ground acceleration. This is denoted by u¨ g(t), where 'u' is the displacement and 'g(t)' indicates the function of time that describes how the ground moves. During an earthquake, buildings must be designed to cope with these external forces, which act upon them as the ground shakes.
Examples & Analogies
Imagine a tall tree swaying in the wind. Just as the wind causes the tree to bend and sway, the ground shaking during an earthquake makes buildings respond in a similar way. The acceleration provides the force that can cause structural components to move.
Solving Modal Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Each modal equation is solved for q i(t) based on this seismic input.
Detailed Explanation
After the ground acceleration is defined, the next step in seismic analysis involves taking the modal equations derived from the modal superposition method. Each mode of vibration (denoted as q i(t)) responds differently to the seismic input. Thus, engineers will solve these equations for each mode to understand how the entire structure will behave under the seismic loading.
Examples & Analogies
Think of each mode like a musician playing in an orchestra. Each musician (mode) has their unique instrument (response) and contributes to the entire symphony (total structure response). Even if the conductor (seismic input) signals a change, each musician plays their part in response to the cue.
Superimposing Individual Modal Responses
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The individual modal responses are then superimposed to obtain the total structural response.
Detailed Explanation
After obtaining the response of each individual mode to the seismic input, the next step is to add these responses together. This process is known as superposition, which allows engineers to predict the total structural response as a combination of the contributions from all the modes. It simplifies the complex interaction of different vibrating patterns into one comprehensive understanding of how the structure will behave during an earthquake.
Examples & Analogies
Imagine a group of friends trying to lift a heavy couch. Each person (mode) pulls on a different part of the couch (the structure), but together they lift it as a team (superimposition of responses). The total effort of all the friends working together determines whether the couch moves or stays put.
Considerations for Mode Selection
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Considerations:
- Only a limited number of modes (typically the first 3 to 5) are sufficient to capture most of the seismic response.
- Higher modes may have negligible contribution for low-rise structures but become important for tall buildings or flexible structures.
Detailed Explanation
When performing seismic analysis, engineers must decide how many modes to consider—usually between 3 to 5 primary modes are sufficient for most structures. However, in taller or more flexible buildings, higher modes may become more significant, highlighting that sometimes what seems less important in one structure could be essential for another.
Examples & Analogies
Think of a ladder with several rungs. For a short ladder, you only need to pay attention to the lower rungs (lower modes) to get stable support. But for a taller ladder, you might have to grip higher up (consider more modes) to maintain balance and avoid tipping over.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Ground Acceleration: The input force acting on structures during earthquakes.
-
Mode Superposition Method: A technique that breaks down complex dynamic responses into simpler solutions for easier analysis.
-
Modal Response: Individual contributions from each vibration mode, helping to develop the total structural response.
-
Total Structural Response: The result of superimposing all modal responses.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example 1: A low-rise building may only need the first 3 modes to capture 90% of the expected seismic response.
-
Example 2: A tall skyscraper may require the analysis of up to 15 modes to fully account for its dynamic behavior during an earthquake.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the quake so bold, the ground does shake, / Modes come together, for safety's sake.
📖 Fascinating Stories
-
Imagine a tall building during an earthquake. It doesn't just shake; it dances in various modes, some moves are significant, others less so. The architect knows to focus on the main dance moves, capturing the essence of the building's response without losing detail.
🧠 Other Memory Gems
-
S-M-O-D helps you remember the steps: Seismic response, Modal responses, Overlap, Decompose.
🎯 Super Acronyms
GAMP for Ground Acceleration, Modal Response, and Superposition for clarity in seismic analysis.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Ground Acceleration
Definition:
The acceleration of the ground during seismic activities, acting as the external force on structures.
-
Term: Mode Superposition Method
Definition:
An analytical technique that simplifies dynamic responses of MDOF systems by decomposing them into SDOF responses.
-
Term: Modal Response
Definition:
The response of a structure associated with each specific vibration mode.
-
Term: Seismic Response
Definition:
The overall response of a structure to seismic loading, including displacements and vibrations.
-
Term: MDOF System
Definition:
Multi-Degree-Of-Freedom system where multiple masses are interconnected, responding to dynamic loads.
-
Term: SDOF System
Definition:
Single-Degree-Of-Freedom system representing a simplified response for a specific mode.