Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Requirement for Modal Data
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s look at the second limitation: the requirement for modal data. What do you think 'modal data' entails?
Is it the frequencies and mode shapes of the structure?
Exactly! Modal data is crucial for performing deformation analyses using the Mode Superposition Method. However, this data can be difficult to obtain, especially for complex and irregular structures.
So, what do we do if we can't obtain it?
In such cases, engineers may have to rely on simulations or approximations that could compromise the reliability of the analysis.
Does that mean we can't use this method for many real-world structures?
Not necessarily! While it's a challenge, engineers still often use this method. They just need to be cautious and supplement it with other analyses to ensure accuracy.
Ignoring Higher Modes
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s delve into the third limitation regarding higher modes. Why might ignoring these modes lead to problems in our analysis?
Because in tall buildings, the first few modes might not capture all the vibrations?
Exactly! Higher modes can play a significant role, particularly in tall or irregular structures, affecting their seismic response. Ignoring them can lead to approximation errors.
So how do we know if we’re ignoring important modes?
Good question! Engineers usually perform a modal analysis to determine the contributions of the first few modes and compare them to higher modes. If necessary, they can include more modes to ensure comprehensive coverage, typically aiming for modes that capture at least 90% of the mass participation.
I see! It's about balancing computational efficiency and accuracy.
Exactly! Always evaluate the trade-off between complexity and analysis depth. Excellent discussion today!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses the limitations of the Mode Superposition Method in structural analysis, highlighting challenges with highly nonlinear systems, the requirement for modal data, and potential errors from ignoring higher modes in irregular structures, which could impact accuracy in seismic response analysis.
Detailed
Limitations of the Mode Superposition Method
The Mode Superposition Method is a powerful analytical approach for structural dynamics, particularly in analyzing multi-degree-of-freedom (MDOF) systems. However, there are several critical limitations that practitioners should be aware of:
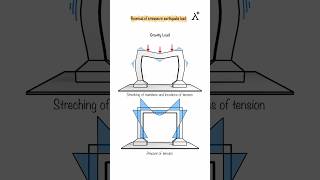
- Nonlinearity Constraint: The method is primarily applicable to linear systems. It requires linearization when applied to highly nonlinear systems, which may distort actual structural behavior during dynamic loading events.
- Modal Data Requirement: The method necessitates detailed modal data (natural frequencies and mode shapes), which may not be easily obtainable for irregularly shaped structures without extensive modeling.
- Higher Modes Ignored: Often, only the first few modes are considered in analysis, which may lead to significant approximation errors, especially in tall or irregular structures where higher modes can drastically influence the response.
Understanding these limitations is crucial for engineers and designers to ensure the accuracy and reliability of seismic assessments and structural evaluations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Nonlinearity in Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Not suitable for highly nonlinear systems unless linearized.
Detailed Explanation
The Mode Superposition Method relies on the assumption that structural behavior can be accurately described using linear equations. In real-world applications, many structures, especially under extreme loading conditions like earthquakes, may exhibit nonlinear behavior. This means that as forces increase, the response of the structure does not remain proportional to the forces applied. This limitation is crucial to understand because if engineers apply this method to systems that become highly nonlinear, the results would be unreliable unless such nonlinearity is simplified or linearized.
Examples & Analogies
Imagine a rubber band; if you stretch it a little, it returns to its original shape (linear behavior). However, if you stretch it too much, it may not return to its original form (nonlinear behavior). Just like that, structures can behave differently as they are pushed beyond normal limits.
Requirement for Modal Data
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Requires modal data (frequencies and mode shapes), which may not be available for irregular structures without modeling.
Detailed Explanation
For the Mode Superposition Method to function properly, it requires knowledge about the modal properties of the structure—this includes the natural frequencies and the mode shapes. However, for complex or irregular structures that do not have a straightforward design, obtaining these modal properties can be challenging. Often, these details need to be established through complex modeling and analysis before the superposition method can be applied effectively.
Examples & Analogies
Think of trying to cook a new recipe without knowing the exact measurements or ingredients required. Just as you can’t bake a cake perfectly without the recipe, you can't effectively analyze a structural response without knowing its modal characteristics.
Ignoring Higher Modes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Higher modes may be ignored, which could lead to approximation errors in tall or irregular structures.
Detailed Explanation
In the application of the Mode Superposition Method, engineers often focus only on the first few modes of vibration, typically the first three to five. This approach is based on the understanding that these modes contribute the most to the overall structural response. However, in tall or irregular structures, the higher modes might play a significant role in how the structure reacts to dynamic forces, such as those experienced during an earthquake. Failing to include these higher modes can lead to inaccurate predictions of the structure's response, potentially risking safety and performance.
Examples & Analogies
Consider a stringed musical instrument. When you pluck a guitar string, it vibrates in a fundamental frequency and also produces higher harmonics. If you only listen to the fundamental sound, you miss the richer tones that make the music complete, much like how ignoring higher modes can mask critical responses in structural dynamics.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mode Superposition Method: A technique to simplify the dynamic behavior of structures by analyzing independent modal responses.
-
Nonlinear Systems: Structures that do not follow linear behavior, which complicates analysis and application of the mode superposition method.
-
Modal Data: Essential frequencies and mode shapes required to perform modal analysis effectively.
-
Ignoring Higher Modes: A potential source of approximation error in dynamic response predictions, especially for tall or irregular structures.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
In a traditional building design, engineers may neglect higher modes when analyzing a structure under seismic loading, which may lead to underestimating the response for taller buildings.
-
For a bridge subjected to dynamic tidal forces, ignoring certain modal contributions can cause inaccuracies in assessing the bridge's resilience to wave impacts.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a structure's dance, modes take their chance, don't ignore the higher, or lose the balance.
📖 Fascinating Stories
-
Imagine a tall building swaying in the wind; without accounting for all its dancing modes, it might lose its stand.
🧠 Other Memory Gems
-
Remember the acronym 'NIM': N (Nonlinear behavior), I (Importance of modal data), M (Modes not to ignore).
🎯 Super Acronyms
LIM
- Limitations (Nonlinear concern)
- Irregular data (modal necessity)
- and Modes ignored lead to error.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mode Superposition Method
Definition:
An analytical technique used in structural dynamics to break down complex responses of multi-degree-of-freedom systems into simpler single-degree-of-freedom responses.
-
Term: Nonlinear Systems
Definition:
Systems where the behavior does not follow a linear relationship between cause and effect, complicating the analysis.
-
Term: Modal Data
Definition:
Information regarding the natural frequencies and mode shapes of a structure necessary for dynamic analysis.
-
Term: Higher Modes
Definition:
Modes of vibration that occur at higher frequencies, which can significantly affect the response of tall or irregular structures.