Concept of Mode Superposition - 18.3
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mode Superposition
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we are going to explore the Mode Superposition Method. Can anyone tell me what this method is generally used for?

Is it used to analyze how structures respond to dynamic loads like earthquakes?

Exactly! It helps us break down complex responses into simpler modal responses. What do we mean when we refer to structural response?

It's how the structure vibrates or moves under forces, right?

Correct! We express the displacement as a linear combination of mode shapes and time-dependent coefficients. Who can explain what a mode shape is?

A mode shape indicates the pattern of vibration for a specific frequency.

Great job! Remember that each structure has multiple mode shapes based on its natural frequencies.

So, by using these modes, we can simplify the analysis process?

Yes, exactly! The simplification makes it much more manageable to analyze MDOF systems.

Let's recap: the Mode Superposition Method decomposes total displacement into modal contributions, simplifying complex structural response analysis.
Orthogonality of Modes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let’s discuss the orthogonality of modes. Can someone explain its importance?

Is it related to how we keep the different modes independent?

Absolutely! The orthogonality properties mean that the inner product of different mode shapes is zero, which helps us simplify our calculations significantly. What else does this allow us to do?

It helps us uncouple the equations of motion, right?

That's right! By employing this property, we isolate each mode for easier analysis.

So we treat each mode separately as independent systems?

Exactly! Each mode can be analyzed as its own SDOF system, which greatly simplifies our work.

Remember: the orthogonality conditions relate to both the mass and stiffness matrices. When combining these, we can gain insights into dynamic behavior.
Application in Seismic Analysis
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s shift our focus to one of the critical applications of the Mode Superposition Method: seismic analysis. Why do we analyze structures for seismic loading?

To ensure they can withstand earthquakes without collapsing, right?

Exactly! In seismic analysis, we apply ground acceleration as an external force. How do we apply the mode superposition method here?

We solve each modal equation individually based on the ground acceleration?

Yes! After solving for each modal response, we superimpose them to get the total structural response.

Do we always need to consider all modes?

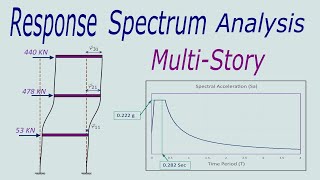
Great question! Typically, the first few modes capture most of the response, often just 3 to 5, depending on the structure.

Let’s recap: In seismic analysis, we express the ground acceleration as an input, solve for modal responses, and superimpose them to evaluate structural behavior.
Advantages and Limitations
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we've discussed the method, what do you think are some advantages of using the Mode Superposition Method?

It reduces the computational effort since we’re solving uncoupled systems.

Absolutely! It provides insights into dynamic behavior. However, are there any limitations to be aware of?

It might not be suitable for nonlinear systems, right?

Correct! And we must also have accurate modal properties available, or we might face issues.

Are there cases where we can overlook important modes?

Exactly! If we ignore higher modes, especially in tall or irregular structures, it may introduce significant errors.

Remember: The key advantages are computational efficiency and clarity in understanding dynamic behavior, while limitations include the requirement for linearity and the need for accurate modal data.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In the analysis of structures subject to dynamic loading, the Mode Superposition Method decomposes the overall response into contributions from individual natural modes of vibration. This method facilitates the understanding and calculation of structural dynamics, especially for seismic loading, by allowing engineers to analyze multi-degree-of-freedom systems efficiently.
Detailed
Concept of Mode Superposition
The Mode Superposition Method simplifies the dynamic analysis of structures by allowing engineers to express total displacement as a sum of individual modal responses. In this method, the total dynamic response is represented as a linear combination of mode shapes and corresponding time-dependent modal coordinates. The method capitalizes on the orthogonality of modes, which allows for uncoupling the equations of motion for multi-degree-of-freedom (MDOF) systems into independent single-degree-of-freedom (SDOF) systems. This is particularly useful in seismic analysis, where only the first few modes are often sufficient to capture the majority of the structural response. The method is widely used in modern software applications and aids in ensuring effective seismic design and performance evaluation.
Youtube Videos








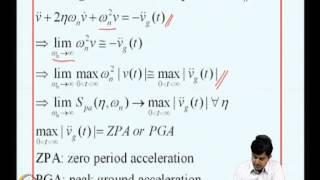
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Modal Decomposition
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The total displacement u(t) is expressed as a linear combination of mode shapes:
$$u(t)=\sum_{i=1}^{n} \phi_i \cdot q_i(t)$$
where:
- $\phi_i$ = mode shape vector of the ith mode
- $q_i(t)$ = time-dependent modal coordinate (amplitude) for mode i
- n = number of significant modes considered
Detailed Explanation
In the mode decomposition step, we express the overall movement of the structure, denoted as u(t), as a combination of different mode shapes that describe how the structure can vibrate. Each mode shape corresponds to a particular vibration pattern, and the coefficients (q_i(t)) tell us how much of each pattern is involved at any time. We consider only 'n' modes that significantly influence the structure's response.
Examples & Analogies
Think of a musical instrument, like a guitar. When you pluck a string, it vibrates in different modes. The fundamental frequency (the basic sound) is the first mode, while higher pitches are higher modes. The sound you hear is a blend of these vibrations, much like how a building vibrates in different modes during an earthquake.
Orthogonality of Modes
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Mode shapes are orthogonal with respect to both the mass and stiffness matrices:
$$\phi_i^T M \phi_j = 0 \quad \text{and} \quad \phi_i^T K \phi_j = 0 \quad \text{for } i \neq j$$
Detailed Explanation
The orthogonality of modes means that different modes do not interfere with each other, allowing us to analyze them independently. Mathematically, when you take the product of different mode shapes with the mass or stiffness matrices, you get zero. This property simplifies calculations and allows us to treat the response of each mode as a separate, independent system.
Examples & Analogies
Imagine you are in a room full of musicians, each playing a different instrument. If they play different notes, their sounds don't overlap or disrupt each other. This is similar to how different vibration modes in a structure operate; each mode vibrates without affecting the others, simplifying how we can study them.
Uncoupling of Equations
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Substituting the modal decomposition into the equations of motion and using orthogonality results in uncoupled equations, each representing an independent SDOF system.
Detailed Explanation
After expressing the displacement in terms of individual modes, we substitute this expression into the governing equations of motion. Thanks to the orthogonality property, we can dissociate the complex equations into simpler equations, where each equation describes one single-degree-of-freedom (SDOF) system rather than a multi-degree-of-freedom (MDOF) system. This greatly simplifies the mathematical problem we must solve.
Examples & Analogies
Think of a jigsaw puzzle. When you tackle the puzzle by focusing on one piece at a time, the task becomes manageable. In a similar way, uncoupling equations allows engineers to解决volve one mode at a time instead of dealing with the complexity of all modes together, making it much easier to understand how the structure will behave.
Key Concepts
-
Modal Decomposition: The sum of modal shapes and coordinates representing total response.
-
Orthogonality: Modes can be treated independently due to their orthogonality, which simplifies calculations.
-
Dynamics: The method aids in understanding the dynamic behavior of structures under various loads.
Examples & Applications
When analyzing a multi-story building during an earthquake, engineers may only analyze the first three modes to obtain a reasonable estimate of the structure's response.
In a bridge design, the first few modes account for the majority of vibrations when subjected to wind or seismic forces.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When structures sway from a quake's might, the modes will guide their dance with light.
Stories
Imagine a building at a concert where each floor feels the beat. Each floor has its own way of moving, creating an overall rhythm - that's each mode in action!
Memory Tools
Modes Are Organizational DiploMats, each representing a unique way structures sway (MAODMS).
Acronyms
MOP
Modal Observation Process - for piecing together modal contributions.
Flash Cards
Glossary
- Mode Superposition Method
An analytical technique for breaking down complex structural responses into simpler modal contributions in the analysis of dynamic loading.
- Modal Decomposition
The process of expressing total displacement as a linear combination of natural mode shapes.
- Orthogonality
The property that indicates that different mode shapes are independent of each other, allowing for simplification in calculations.
- Modal Analysis
The study of a structure's dynamic characteristics by analyzing its natural frequencies and mode shapes.
- MultiDegreeofFreedom System (MDOF)
A system with multiple interdependent movements or vibrations, such as a complex structure with many components.
- SingleDegreeofFreedom System (SDOF)
A simplified system that can be described by a single coordinate for motion or vibration.
Reference links
Supplementary resources to enhance your learning experience.
