Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding MDOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Alright class, today we are diving into Multi-Degree-of-Freedom systems. Can anyone tell me what an MDOF system is?
Isn't it a structure with multiple interconnected parts?
Exactly! MDOF systems consist of multiple masses connected by stiffness elements. Think of a building with various floors as an MDOF system. Why do you think understanding this concept is important during dynamic loading events, like earthquakes?
It’s important because buildings will behave differently than we expect during such events!
Yes! They respond in various modes, not just one. And we will see how we can analyze this with the Mode Superposition Method. This method breaks down the complex response into simpler parts, making analysis easier.
How do we express the motion of MDOF systems mathematically?
Great question! The generalized equation of motion is expressed as: $ Mu¨(t) + Cu˙(t) + Ku(t) = F(t) $ where M represents the mass matrix, C is the damping matrix, and K is the stiffness matrix. Understanding this equation is the first step in analyzing MDOF systems.
So, in summary, MDOF systems consist of multiple interconnected masses and their motion is described using a system of equations that require us to consider the coupling between these masses.
Challenges of MDOF Systems
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let's discuss the challenges we face in analyzing MDOF systems directly. Why do you think that may be?
It sounds complicated! Is it because there are so many equations?
Yes, the interactions cause coupling among equations, making direct solution challenging. However, the Mode Superposition Method provides a way to simplify this.
How does the Mode Superposition Method work in uncoupling these equations?
The method decomposes the total response into individual modal responses, allowing us to analyze them separately. It provides a clear way to handle the dynamic response due to external forces.
Can we use this for all types of structures?
Great question! The method is best suited for linear systems. For highly nonlinear systems, we would need to do some linearization first. Always important to keep that in mind!
In summary, while MDOF systems are complex due to their interconnected masses, the Mode Superposition Method simplifies our analysis significantly by allowing us to view each mode independently.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section introduces MDOF systems, emphasizing their complex dynamic behavior due to multiple masses and stiffness elements. It describes the equation of motion for MDOF systems and indicates the challenges in direct solutions while highlighting the purpose of the Mode Superposition Method for uncoupling the equations and simplifying analysis.
Detailed
Multi-Degree-of-Freedom (MDOF) Systems
In the realm of structural dynamics, MDOF systems are critical as they represent structures such as buildings and bridges which do not respond in a simple manner due to their interconnected masses (e.g., floors) and stiffness elements (e.g., beams and columns). The fundamental equation governing the motion of these systems is given by:
$$ Mu¨(t) + Cu˙(t) + Ku(t) = F(t) $$
Where:
- M is the mass matrix,
- C is the damping matrix,
- K is the stiffness matrix,
- u(t) is the displacement vector,
- F(t) is the external force vector, potentially due to seismic activities.
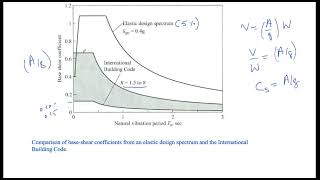
The challenge in solving this equation directly arises from the coupling of these equations, as MDOF systems exhibit complex interactions. The Mode Superposition Method serves as an elegant solution by decomposing the dynamic response of the MDOF system into simpler single-degree-of-freedom (SDOF) responses, enabling easier uncoupling and analysis. This method is especially significant in the design and evaluation of structures subjected to dynamic loading, simplifying what would otherwise be an intricate problem.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definition of MDOF Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Structures like buildings and bridges behave as MDOF systems, where multiple masses (floors or segments) are interconnected by stiffness elements (columns or structural members).
Detailed Explanation
MDOF systems refer to structures that have multiple degrees of freedom, meaning they can move in several ways simultaneously. Each part of the structure, such as floors in a building or sections of a bridge, acts like a mass that can vibrate independently or in conjunction with others. These components are linked by materials, like beams or columns, that provide stiffness, allowing the entire structure to maintain its shape while it vibrates.
Examples & Analogies
Imagine a group of friends holding hands while dancing. Each friend (representing a mass) can move their arms or legs (representing different degrees of freedom) independently, but they remain connected by holding hands (the stiffness elements). This analogy helps visualize how MDOF systems function, as each part moves but is still part of the whole.
Equation of Motion for MDOF Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Equation of Motion (conceptual): M ü(t) + C u˙(t) + K u(t) = F(t) where:
- M is the mass matrix
- C is the damping matrix
- K is the stiffness matrix
- u(t) is the displacement vector
- F(t) is the external force vector (e.g., seismic forces)
Detailed Explanation
The motion of an MDOF system can be described using a mathematical equation called the 'Equation of Motion.' In this equation, 'M' represents how much mass is present in different parts of the structure, 'C' accounts for energy loss due to damping (like friction or air resistance), and 'K' describes the stiffness, or how resistant the structure is to deformation. 'u(t)' indicates how far the structure moves from its original position at any given time, while 'F(t)' represents external forces acting on the structure, such as those from an earthquake.
Examples & Analogies
Think of riding a bike over rough terrain. The bike frame (stiffness) is rigid, minimizing flex. The weight of the bike and rider (mass) determines how quickly it accelerates or slows down when you hit bumps (external forces). Damping, like the suspension system on the bike, reduces how harshly you feel each bump. This relationship in the bike can be analogous to larger structures like buildings under dynamic loads.
Challenges of Direct Solution
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Solving this equation directly is often complex due to the coupling of equations. Mode Superposition provides an elegant approach to uncouple and solve them.
Detailed Explanation
When attempting to solve the equation of motion for an MDOF system directly, complications arise because the equations are interconnected or 'coupled.' This means the response of one mass affects the others, making it difficult to analyze each mass's behavior independently. The Mode Superposition Method is introduced to simplify this process by allowing us to break down the complex equations into simpler, uncoupled ones, making the calculations more manageable.
Examples & Analogies
Imagine trying to untangle a set of colorful strings knotted together. If you tackle only one string without considering how it interacts with the others, you might end up making the knots tighter. Similarly, MDOF systems are interconnected like tangled strings. The Mode Superposition Method helps you work on each string individually by first smoothening out the overall tangle, allowing for simpler solutions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
MDOF Systems: Structures that consist of multiple interconnected masses and stiffness elements that behave dynamically.
-
Equation of Motion: The representation of the dynamic behavior of MDOF systems in matrix form.
-
Mode Superposition: A technique that simplifies the analysis of MDOF systems by allowing responses to be analyzed independently.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A skyscraper can be modeled as an MDOF system where each floor acts as a separate mass connected by beams acting as stiffness elements.
-
When analyzing for seismic loads, engineers will apply the Mode Superposition Method to determine how each floor of a structure vibrates.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
MDOF systems sway and sway, connected masses lead the way.
📖 Fascinating Stories
-
Imagine a tall building swaying during an earthquake. Each floor is a mass that reacts, connected by strong beams—this is how structural integrity relies on MDOF systems.
🧠 Other Memory Gems
-
MDOF stands for Modes, Degrees, and Oscillation Frequencies.
🎯 Super Acronyms
MDOF
- Masses
- Damping
- Oscillation Framework.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: MultiDegreeofFreedom (MDOF) System
Definition:
A structural system with multiple masses and stiffness elements interconnected, having complex dynamic responses.
-
Term: Equation of Motion
Definition:
Mathematical representation of the dynamics of a system, usually stated in the form of M, C, K matrices.
-
Term: Mode Superposition Method
Definition:
Analytical technique used to decompose the response of MDOF systems into simpler SDOF responses.
-
Term: Mass Matrix (M)
Definition:
A matrix representing the mass distribution of a structure in an MDOF system.
-
Term: Stiffness Matrix (K)
Definition:
A matrix representing how a structure resists deformation.
-
Term: Damping Matrix (C)
Definition:
A matrix that characterizes how the structure dissipates energy during vibrations.