Earthquake Recurrence and Return Period
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Recurrence Interval
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to learn about the recurrence interval of earthquakes. Can anyone tell me what a recurrence interval is?

Is it the time between two earthquakes?

Exactly! The recurrence interval is the average time between two large earthquakes on the same fault segment. It's essential for understanding how often earthquakes happen.

How do we measure that?

Great question! We can calculate it using paleoseismology, which looks at geological layers, as well as historical records of seismic events. Let's remember P.A.H—Paleoseismology, Archaeological data, and Historical records, for how we gather these data.

So, it’s like digging back in time!

Yes, that's a fun way to put it! Now, let's think about why knowing the recurrence interval is important.

It helps in predicting future earthquakes, right?

Exactly! It helps us assess risks and plan for safety measures.

To sum up today’s lesson, the recurrence interval provides insights into the timing of earthquakes, obtained through various data sources.
Exploring the Gutenberg-Richter Relationship
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we understand recurrence intervals, let's move to the Gutenberg-Richter relationship. Can someone explain what that is?

Isn't it about how often earthquakes of different magnitudes happen?

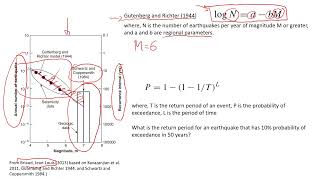
Correct! The Gutenberg-Richter relationship shows how the number of earthquakes relates to their magnitudes. The formula is Log(N) = a – bM. Who can explain what N, a, and b represent?

N is the number of earthquakes, right? But what about a and b?

Exactly! N is the number of earthquakes greater than or equal to a given magnitude M. The constants a and b vary by region. Remember this by thinking of A-B-C—Earthquake statistics by Area and B-value being regional. They are crucial for assessing earthquake hazard!

So, this helps us know which earthquakes are likely to happen?

Yes! It informs us about the likelihood of different magnitudes of earthquakes occurring. Summarizing today: The Gutenberg-Richter relationship helps us understand the frequency and magnitude of seismic events.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section elaborates on the recurrence interval, which is the average time between large earthquakes on the same fault segment, emphasizing its calculation through paleoseismology, historical data, and fault slip rates. It also introduces the Gutenberg-Richter relationship, linking the number of earthquakes to their magnitudes, demonstrating a key relationship in seismic studies.
Detailed
Earthquake Recurrence and Return Period
In studying seismic hazards, understanding the timing of earthquakes is crucial. This section highlights two important concepts:
Recurrence Interval
The recurrence interval is defined as the average time between two large earthquakes on the same fault segment. This interval can be derived from various sources, including paleoseismological studies that analyze geological layers, historical records that document past seismic events, and measurements of the fault slip rate, which helps estimate how quickly energy accumulates along a fault line. Understanding recurrence intervals is essential for assessing risks and planning for future earthquakes.
Gutenberg-Richter Relationship
The Gutenberg-Richter relationship is a statistical model that describes the distribution of earthquake magnitudes in a given region. It is expressed through the formula:
Log(N) = a – bM where:
- N is the number of earthquakes of magnitude greater than or equal to M.
- a and b are constants specific to the region studied.
This relationship provides insights into the frequency of earthquakes of different magnitudes, which is crucial for hazard assessment and reinforcing the need for earthquake preparedness.
The importance of recurrence intervals and the Gutenberg-Richter relationship cannot be overstated; they form the foundation for anticipating future seismic events and implementing effective engineering practices in earthquake-prone areas.
Youtube Videos



![[BCT2025 Webinar] Long Period Ground Motion in Earthquake – its Impacts, Measures and Effects 1](https://img.youtube.com/vi/0lGZlFHEbS4/mqdefault.jpg)



Audio Book
Dive deep into the subject with an immersive audiobook experience.
Recurrence Interval
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The average time between two large earthquakes on the same fault segment. Based on paleoseismology, historical records, and fault slip rate.
Detailed Explanation
The recurrence interval refers to the average time lapse between two significant earthquakes that occur along the same fault line. This interval is determined through the study of past earthquakes (paleoseismology) as well as documented historical records of seismic activity. Scientists also consider how quickly the tectonic plates are moving (fault slip rate) to better estimate this interval. Understanding recurrence is crucial for predicting the likelihood of future earthquakes and for developing safety measures in earthquake-prone areas.
Examples & Analogies
Imagine a train arriving at a station at consistent intervals. If the train arrives every 10 minutes, we can expect it to arrive at that regularity. Similar to this scenario, scientists calculate how often earthquakes 'arrive' based on historical data, which helps them predict when the next earthquake might occur.
Gutenberg-Richter Relationship
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Log(N) = a – bM Where:
– N = number of earthquakes greater than or equal to magnitude M
– a, b = region-specific constants.
Detailed Explanation
The Gutenberg-Richter relationship is a mathematical formula that expresses the frequency of earthquakes in relation to their magnitude. In this relationship, 'N' represents the number of earthquakes that are equal to or exceed a certain magnitude 'M'. The constants 'a' and 'b' are specific to geographical regions and are used in the equation to provide a better fitting to the observed seismic data. This formula helps seismologists understand patterns in earthquake occurrence and can be pivotal for hazard estimates and planning.
Examples & Analogies
Think of this relationship like a bakery selling different sizes of cakes. If the bakery sells mostly small cakes, fewer large cakes will be available. Similarly, in seismology, most earthquakes are minor, and only a few reach high magnitudes. The Gutenberg-Richter formula helps predict how many small versus large 'cakes' (earthquakes) to expect based on historical trends.
Key Concepts
-
Recurrence Interval: The average time between large earthquakes on the same fault.
-
Paleoseismology: A method to study past earthquakes.
-
Gutenberg-Richter Relationship: A mathematical model that relates the number of earthquakes to their magnitudes.
Examples & Applications
Historical records show that the San Andreas Fault has an average recurrence interval of about 150 years.
The Gutenberg-Richter relationship was found to hold for many regions, indicating that small earthquakes are much more frequent than large ones.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Earthquake time, oh what a race, Recurrence tells us to embrace.
Stories
Imagine a geologist uncovering layers of earth, revealing the history of earthquakes over centuries, piecing together when the next rumble might happen.
Memory Tools
To remember the Gutenberg-Richter relationship, think 'N is Number, A is Area, B is B-value!'
Acronyms
P.A.H = Paleoseismology, Archaeological data, Historical records for calculating recurrence intervals.
Flash Cards
Glossary
- Recurrence Interval
The average time between two large earthquakes on the same fault segment.
- Paleoseismology
The study of past earthquakes using geological and archeological data.
- GutenbergRichter Relationship
A statistical relationship that describes the distribution of earthquake magnitudes.
- Magnitude
A measure of the energy released by an earthquake.
Reference links
Supplementary resources to enhance your learning experience.
