Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Computational Modelling
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're diving into how computational modelling helps us predict seismic wave behaviors from hypocentres. Can anyone tell me what a hypocentre is?
Isn't it the point inside the Earth where an earthquake starts?
Exactly! And understanding how waves propagate from this point is crucial. Now, why do we need computational models in this context?
To simulate what happens during an earthquake!
Right again! These models allow us to prepare better for earthquakes and design safer structures. Let's explore some specific techniques.
Finite Element Models (FEM)
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
First, we have Finite Element Models, or FEM. These help us understand how primary waves travel through different materials. What do you think happens to the wave speed in rock versus water?
The waves would travel faster in rock because it's denser, right?
Exactly! Knowing how these waves move in different materials assists engineers in predicting potential impacts on buildings. Can anyone relate this to structural safety?
If we know how fast the waves travel, we can determine how much a building might shake!
Great connection! Understanding this allows us to design buildings that can withstand seismic forces.
Ground Motion Prediction Equations (GMPEs)
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s talk about Ground Motion Prediction Equations, or GMPEs. Can anyone describe what they consider GMPEs to do?
They predict how strong the shaking will be at a location based on the earthquake's characteristics!
Exactly! They take into account the depth of the hypocentre and other factors to give us estimates. Why is this important for urban planning?
It helps in identifying which areas need stronger buildings!
You got it! GMPEs are pivotal for making informed decisions about where and how to build.
Strong Motion Data Libraries
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Lastly, let’s discuss Strong Motion Data Libraries. Why do you think they are crucial for our predictive models?
They provide real data to compare against predictions, right?
Exactly! This calibration process ensures our models are as accurate as possible. Can anyone think of a scenario where inaccurate models could lead to problems?
If a model underestimates shaking, buildings might not be built to code, and people could get hurt!
Perfect point! Accurate data helps save lives by ensuring our structures can handle real seismic threats.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we delve into the computational modelling methods employed to predict the behavior of seismic waves originating from earthquake hypocentres. Techniques such as Finite Element Models (FEM) and Ground Motion Prediction Equations (GMPEs) are discussed, highlighting their importance in seismic analysis and structural prediction.
Detailed
Detailed Summary
In the field of earthquake engineering, understanding how seismic waves propagate from hypocentres is crucial for effective disaster planning and structural resilience. This section on computational modelling discusses the various advanced techniques used to simulate seismic events.
Key Techniques:
- Finite Element Models (FEM): These models simulate the propagation of primary waves from the hypocentre through different geological materials, providing insights into how structures might respond to seismic waves.
- Ground Motion Prediction Equations (GMPEs): GMPEs factor in variables such as the depth of the hypocentre, earthquake magnitude, and local soil conditions to estimate potential ground motion at various distances from the epicentre.
- Strong Motion Data Libraries: These libraries are essential for calibrating predictive models against historical seismic data, ensuring that models can accurately represent local seismic behaviors.
Overall, these tools are vital for improving site-specific seismic hazard assessments and contributing to more effective structural designs against seismic impacts.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Computational Modelling
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Advanced computational tools simulate seismic events to predict behavior of structures.
Detailed Explanation
This chunk introduces the importance of advanced computational tools in earthquake engineering. These tools help simulate seismic events, allowing engineers to predict how structures will respond during an earthquake. By using these simulations, engineers can better design buildings and infrastructure to withstand seismic forces.
Examples & Analogies
Think of computational modeling like a video game where players can test different strategies in a safe environment before facing real situations. Just as players learn how to overcome challenges in a game, engineers use simulations to identify potential problems and find solutions for structures in earthquake-prone areas.
Finite Element Models (FEM)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Finite Element Models (FEM) simulate how primary waves propagate from the hypocentre.
Detailed Explanation
Finite Element Models (FEM) are advanced simulations that help visualize how seismic waves, particularly primary waves, travel from the hypocentre through different materials. FEM breaks down complex structures into smaller, manageable parts (or 'elements') to analyze how these pieces respond to seismic forces. This allows for a detailed examination of wave propagation and helps engineers design more resilient buildings.
Examples & Analogies
Consider FEM like a jigsaw puzzle. Just as each piece fits together to form a complete picture, each element in the FEM works together to simulate how seismic waves impact the overall structure. This gives us a clearer understanding of how different parts of a building will react during an earthquake.
Ground Motion Prediction Equations (GMPEs)
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Ground Motion Prediction Equations (GMPEs) include parameters like depth of hypocentre, magnitude, and soil conditions.
Detailed Explanation
GMPEs are mathematical equations that help predict how strongly ground will shake during an earthquake. They take into account various factors, including the depth of the hypocentre, the earthquake's magnitude, and the type of soil in the area. By using GMPEs, engineers can estimate how much shaking buildings will experience and thus design them to withstand that shaking.
Examples & Analogies
Imagine GMPEs as a weather forecast that predicts how windy or rainy it will be. Just like a good forecast considers temperature, humidity, and wind direction, GMPEs consider the depth of the earthquake, its size, and local soil types to predict ground motion.
Strong Motion Data Libraries
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Strong Motion Data Libraries help calibrate these models for local seismic scenarios.
Detailed Explanation
Strong Motion Data Libraries are collections of recorded ground motion data from past earthquakes. Engineers use this data to calibrate and improve their computational models, ensuring that the predictions reflect real-world seismic activity. By comparing model predictions with actual data, engineers can refine their designs and make them safer against potential earthquakes.
Examples & Analogies
Think of this process like an athlete studying game footage to improve performance. Just as athletes analyze their previous games to identify areas for improvement, engineers use data from past earthquakes to enhance their models and ensure structures are more resilient.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
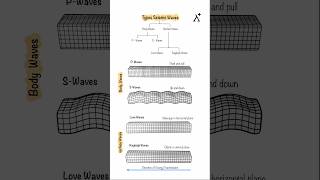
Hypocentre: The point in the Earth where an earthquake rupture starts.
-
Finite Element Models (FEM): Simulations used to predict seismic wave propagation.
-
Ground Motion Prediction Equations (GMPEs): Tools for predicting ground shaking based on earthquake characteristics.
-
Strong Motion Data Libraries: Repositories of seismic data used for model calibration.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An FEM might simulate how seismic waves spread from a hypocentre in different soil types, providing insights for engineers on structural responses.
-
GMPEs can predict that an earthquake with a magnitude of 7.0 at a hypocentre depth of 10 km will likely cause strong shaking in nearby urban areas.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When earthquakes arise, it’s waves that arise; from hypocentre to surface, we must prioritize.
📖 Fascinating Stories
-
Imagine a wave racing to the shore, starting from a point deep below – that’s a hypocentre sending signals galore!
🧠 Other Memory Gems
-
FEMs: Find Each Material’s responses to Earthquake Movements.
🎯 Super Acronyms
GMPE
- Get My Predictions Err... down for seismic evaluations!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Hypocentre
Definition:
The exact point within the Earth where the rupture of an earthquake begins.
-
Term: Finite Element Model (FEM)
Definition:
A computational method used to predict how seismic waves propagate through different geological materials.
-
Term: Ground Motion Prediction Equations (GMPEs)
Definition:
Mathematical equations used to estimate the expected ground shaking resulting from earthquakes based on various parameters.
-
Term: Strong Motion Data Libraries
Definition:
Collections of seismic data used to calibrate models for local seismic scenarios.
-
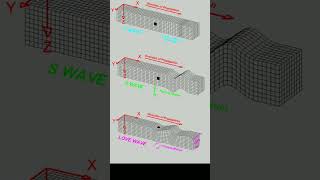
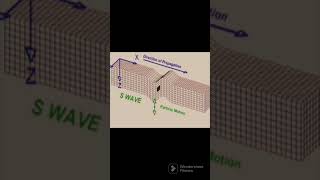
Term: Seismic Waves
Definition:
Energy waves that are generated by earthquakes and propagate through the Earth.