Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Attenuation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're diving into the concept of attenuation, which refers to how earthquake ground motion decreases with distance from the source. Why do you think it's important for us to understand this?
Maybe so we can predict how strong the shaking will be in different places?
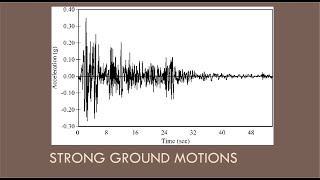
Exactly! Predicting ground shaking helps in designing structures. Attenuation plays a key role in estimating parameters like Peak Ground Acceleration. Can anyone tell me what PGA is?
It’s the maximum acceleration of ground movement?
Correct! It’s crucial for understanding how forces will act on buildings during an earthquake.
Attenuation Equation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let’s look at the general form of the attenuation equation: Y = f(M,R,S). Who can tell me what each symbol represents?
Y is the ground motion parameter, right?
Yes! And what about M, R, and S?
M is the moment magnitude, R is distance from the source, and S is site conditions.
Great! Remember, C₁ to C₅ are empirical constants, which means they come from real data. This means we can adjust predictions based on specific conditions.
Common Attenuation Models
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now, let’s talk about some commonly used attenuation models, like the Boore–Joyner–Fumal model. Why do we have different models?
I guess because different places have different geological features?
Exactly! Each model is tailored to specific regions based on local seismic recordings. Why do you think that’s important?
It ensures that predictions are accurate for that area?
Exactly! Accurate predictions help engineers design buildings that can withstand local earthquake conditions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section introduces the concept of attenuation, explaining how earthquake ground motion diminishes with distance from the source. It outlines the formulae used for estimating seismic parameters such as Peak Ground Acceleration (PGA) and discusses various common attenuation models that apply to specific regions.
Detailed
Attenuation Relationships (Ground Motion Prediction Equations)
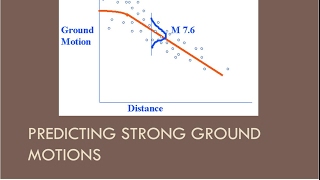
In seismology, attenuation refers to the decrease in ground motion amplitude and energy as distance from the earthquake source increases. This concept is vital for engineers and seismologists who need to predict ground motion parameters like Peak Ground Acceleration (PGA) during an earthquake, which is crucial for designing structures to withstand seismic impacts. The general form of the attenuation equation is given by:
Y = f(M,R,S) = C₁ + C₂M - C₃log(R+C₄) + C₅S
Where:
- Y: Ground motion parameter (e.g., PGA)
- M: Moment magnitude
- R: Distance from the source (epicentral or hypocentral)
- S: Site conditions (such as rock or soil)
- C₁, C₂, C₃, C₄, C₅: Empirical constants derived from seismic studies.
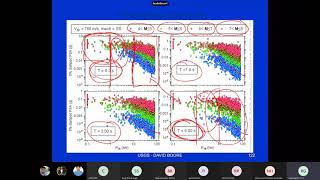
Commonly used attenuation models include the Boore–Joyner–Fumal model, the Campbell model, and the Abrahamson–Silva model, each tailored to specific regions based on local geology and seismic history. Understanding these relationships is essential for seismic hazard analysis and structural response studies.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Attenuation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Attenuation refers to the decrease in earthquake ground motion (amplitude and energy) with increasing distance from the source.
• Used to estimate seismic parameters like Peak Ground Acceleration (PGA), velocity, and displacement at a site.
• Essential for seismic hazard analysis and structural response studies.
Detailed Explanation
This chunk introduces the concept of attenuation in the context of earthquakes. Attenuation means that as you move away from the source of an earthquake, the intensity of ground shaking decreases. This is important because it helps scientists and engineers predict how strong the shaking will be at different distances from the earthquake's origin. The reduction in shaking is not uniform, as it can be influenced by many factors like the type of ground or geological conditions. Moreover, understanding attenuation is vital for evaluating potential dangers to buildings and infrastructure during seismic events.
Examples & Analogies
Think of attenuation like the way sound waves behave. When you’re close to a loudspeaker, the music is very clear and loud. But as you move further away, the sound gets softer and sometimes hard to hear. In the same way, the ground shakes less as you get further from the epicenter of an earthquake. This analogy helps us understand why engineers need to know how strong the shaking will be at different distances.
General Form of Attenuation Equation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Y = f(M, R, S) = C1 + C2 M - C3 log(R + C4) + C5 S
Where:
• Y: Ground motion parameter (e.g., PGA)
• M: Moment magnitude
• R: Distance from source (epicentral or hypocentral)
• S: Site conditions (rock or soil)
• C1, C2,...: Empirical constants
Detailed Explanation
This chunk presents a mathematical model for predicting ground motion parameters, which are influenced by the earthquake's magnitude, the distance from the source, and local site conditions. The equation includes variables: 'Y' represents the ground motion (like Peak Ground Acceleration), 'M' is the earthquake's moment magnitude, and 'R' is the distance from where the earthquake happened. The 'S' term shows how local conditions like soil or rock quality can affect shaking. Each 'C' is an empirical constant that has been determined through research and data analysis, making this equation a useful tool for engineers and scientists.
Examples & Analogies
Imagine you are using a recipe to bake a cake. Each ingredient (butter, sugar, flour) contributes differently to the cake's flavor and texture. In the attenuation equation, each variable (magnitude, distance, site conditions) acts like an ingredient, affecting the final outcome—the shaking you feel during an earthquake. Just as precise amounts of ingredients lead to delicious cakes, using accurate data in this equation leads to better predictions of ground motion.
Commonly Used Attenuation Models
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
• Boore–Joyner–Fumal model
• Campbell model
• Abrahamson–Silva model
These models are region-specific and developed based on seismic recordings and local geology.
Detailed Explanation
Here, we discuss different models used to apply the attenuation equation. Each of these models, such as the Boore–Joyner–Fumal, Campbell, and Abrahamson–Silva models, is designed to give accurate predictions for specific regions based on historical seismic data and geological conditions. They have been adapted over time to account for the unique geological characteristics of each area. This regional adaptation is essential because the effects of an earthquake can vary dramatically in different locations.
Examples & Analogies
Think of these models like different GPS systems for road navigation. Just as some GPS systems are optimized for urban driving while others are better for rural areas, these attenuation models are specifically tailored for certain regions based on local geological features and seismic history.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Attenuation: The decrease in amplitude of ground motion with distance.
-
Ground Motion Prediction Equations: Formulas used to predict ground motion based on various parameters.
-
Empirical Constants: Values derived from real-world data to enhance the accuracy of seismic predictions.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
If a magnitude 6.0 earthquake occurs, the ground motion is predicted using the attenuation equation to determine its intensity at various distances.
-
Different regions may require unique models like the Campbell model for specific geological features.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
As you move away, shaking fades, ground motion dips, so beware!
📖 Fascinating Stories
-
Imagine a child jumping on a trampoline. The nearer you are, the harder you bounce—just like an earthquake! The further away, the softer the shake.
🧠 Other Memory Gems
-
Remember 'MR C' to recall M (Magnitude), R (Distance), C (Conditions) in the attenuation equation.
🎯 Super Acronyms
PGA = Peak Ground Acceleration, where P = Peak, G = Ground, A = Acceleration.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Attenuation
Definition:
The decrease in ground motion amplitude and energy with increasing distance from the earthquake source.
-
Term: PGA
Definition:
Peak Ground Acceleration, the maximum acceleration of ground movement during an earthquake.
-
Term: Moment Magnitude
Definition:
A measure of the energy released at the source of an earthquake, represented in the attenuation equation.