Basic Concepts of Response Spectrum
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Response Spectrum
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we’re starting our discussion with the response spectrum, a critical tool in earthquake engineering. Can anyone tell me what we might measure when we talk about a structure's response?

Is it how much it moves or shakes?

Exactly! We look at the structure's peak responses like displacement, velocity, or acceleration. These tell us how much a structure will move under seismic loads. This is captured in what we call the response spectrum.

How is that different from just measuring the ground motion?

Great question! The response spectrum specifically ties the structure's dynamic properties, like its natural period and damping, to the ground motion. This reflection helps in assessing the design and safety of the building.

What’s the basic equation we use to find this?

The governing equation we often use is mu¨(t)+cu˙(t)+ku(t)=−mu¨ (t)g. It involves mass, damping, and stiffness, helping us to model the response.

So it’s really about understanding how structures react to forces?

Precisely! And understanding these concepts will be fundamental for much of what we will learn in seismic design.

To summarize, a response spectrum illustrates how a structure responds to ground motion through key parameters of displacement, velocity, and acceleration.
Peak Response Parameters
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we've introduced the concepts, let's explore the peak response parameters in detail. Can anyone tell me what parameters we focus on?

Displacement, velocity, and acceleration?

Exactly! We’re talking about the displacement response spectrum (S_d), the velocity response spectrum (S_v), and the acceleration response spectrum (S_a). Each of these provides crucial insight into how a structure might behave during an earthquake.

How are these spectra typically plotted?

They’re plotted against the natural period (T) or frequency (ω) of the system. It’s important to visualize them because it helps us gauge the dynamic response effectively.

What does this help us accomplish in practical terms?

Understanding these parameters helps engineers design structures that can safely withstand seismic events, ensuring safety and compliance with design codes.

So, to recap, the three key parameters—displacement, velocity, and acceleration—are essential for understanding peak responses of a structure during seismic activity.
Importance of SDOF Systems
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s discuss why single-degree-of-freedom systems (SDOF) are significant when we talk about response spectra.

Why focus on SDOF systems?

SDOF systems simplify the analysis of structures under dynamic loading. Their behavior can be analyzed easily, granting us insights that can be generalized to more complex systems.

Does that mean real structures are SDOF systems?

Not necessarily. Real structures are often more complex, but we can use SDOF as a foundational model to gain valuable insights into their response.

So, it helps with initial assessments?

Yes! By understanding SDOF behavior, we can predict how multi-degree-of-freedom systems will react overall. So, SDOF analysis forms a critical basis for building more complex models.

In summary, while actual buildings are more complex, using SDOF systems provides essential insights for initial design and analysis in seismic engineering.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section details how the response spectrum is formulated from the behavior of single-degree-of-freedom (SDOF) systems during seismic events. It explains peak response parameters such as displacement, velocity, and acceleration spectra, enhancing understanding of structural response to dynamic loads.
Detailed
Basic Concepts of Response Spectrum
In the field of earthquake engineering, the response spectrum serves as a vital tool for depicting how structures interact with dynamic seismic loads. This section elaborates on constructing a response spectrum derived from the behavior of single-degree-of-freedom (SDOF) systems under ground motion. The governing equation incorporates mass, damping, and stiffness to model the resulting relative displacement (u(t)), ground acceleration (u¨(t/g)), and crucially outlines the three peak response parameters: displacement response spectrum (S_d), velocity response spectrum (S_v), and acceleration response spectrum (S_a). Each parameter is meticulously plotted against the system's natural period (T) or frequency (). Understanding these parameters is key for engineers in designing safe structures capable of withstanding seismic forces.
Youtube Videos






Audio Book
Dive deep into the subject with an immersive audiobook experience.
Response Spectrum Overview
Chapter 1 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
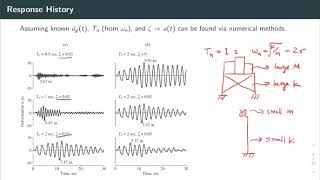
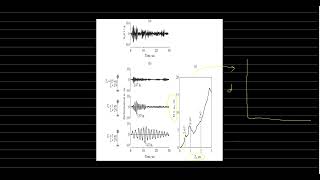
A response spectrum is built from the dynamic response of an SDOF system subjected to a ground motion.
Detailed Explanation
A response spectrum represents how a structural system, modeled as a Single-Degree-of-Freedom (SDOF), responds to ground motion caused by an earthquake. The term 'dynamic response' refers to how the system reacts dynamically to external forces, in this case, the ground shaking. The response spectrum allows engineers to visualize this response in terms of peak values such as displacement, velocity, or acceleration based on the natural frequency and properties of the system.
Examples & Analogies
Think of a swing in a children's playground. When you push the swing, it responds by moving back and forth. The way it swings depends on how hard you push it and its own characteristics (like how heavy it is and how much it resists movement). Just like this swing, buildings respond differently to the forces acting on them like earthquakes, and a response spectrum helps measure that.
Governing Equation for SDOF Systems
Chapter 2 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Governing equation: mu¨(t)+cu˙(t)+ku(t)=−mu¨ (t)g where: o u(t): Relative displacement o u¨(t): Ground acceleration g o m,c,k: Mass, damping, and stiffness
Detailed Explanation
The governing equation of motion for an SDOF system describes how the displacement of the system (u(t)) is influenced by forces such as mass (m), damping (c), and stiffness (k). In this equation: - 'mu¨(t)' represents the inertial force due to the mass and its acceleration. - 'cu˙(t)' represents the damping force, which resists the motion. - 'ku(t)' is the elastic restoring force that tries to bring the system back to its equilibrium position. Finally, the term on the right represents the ground acceleration, which is what causes the motion in the first place.
Examples & Analogies
Imagine a car on a bumpy road. The mass of the car (m) is pushed up and down by the bumps (ground acceleration), while the suspension system helps dampen the motion (damping, c) and keeps the car from bouncing too much by restoring it to its level position (stiffness, k). This equation reflects the car's response to the bumps, similar to how a building responds to earthquakes.
Peak Response Parameters
Chapter 3 of 3
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
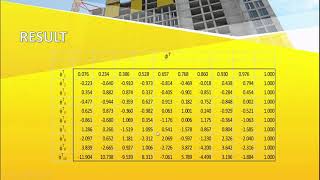
- Displacement response spectrum S_d * Velocity response spectrum S_v * Acceleration response spectrum S_a Each parameter is plotted against the natural period T or frequency ω of the system.
Detailed Explanation
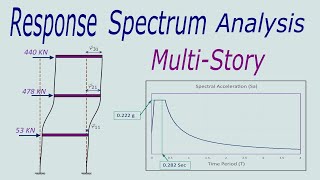
The peak response parameters include three main types of spectra: - Displacement response spectrum (S_d) shows the maximum displacement experienced by the structure; - Velocity response spectrum (S_v) shows the maximum velocity of the structure during motion; - Acceleration response spectrum (S_a) indicates the maximum acceleration. These parameters are plotted against the natural period (T) or frequency (ω), which helps engineers assess how structures behave under various dynamic loads.
Examples & Analogies
Consider a game where you throw different balls (each representing a different structure) from the same height (ground motion). Each ball will bounce to a different maximum height (displacement), speed (velocity), and force of bounce (acceleration) based on its type. Just as the balls react differently based on their properties, buildings also respond differently to earthquakes, and we use the response spectra to characterize those reactions.
Key Concepts
-
Response Spectrum: A graphical representation of how a structure responds to seismic activity.
-
SDOF Systems: A model that simplifies a structure's behavior to one degree of freedom.
-
Peak Response Parameters: The parameters that include displacement, velocity, and acceleration in the context of dynamic load analysis.
Examples & Applications
An example of a response spectrum could be a graph showing how a building with a natural period of 0.5 seconds would experience maximum displacement of 0.2 meters during an earthquake.
In a case where a bridge experiences an acceleration spectrum with peaks at particular frequencies, engineers can devise strategies to mitigate those acceleration forces.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In shaking ground, we look around; responses peek, a spectrum found.
Stories
Imagine a flexible tree swaying during a storm; the way it bends and sways is much like how a building moves in an earthquake, and the response spectrum captures that movement.
Memory Tools
DVA: Displacement, Velocity, Acceleration - the three keys to analyzing how we sway under seismic stress.
Acronyms
SDA
SDOF
Displacement
Acceleration - remember this for peak response analysis.
Flash Cards
Glossary
- Response Spectrum
A graph that depicts the peak response of a structure under dynamic loading, typically represented in terms of displacement, velocity, or acceleration.
- SingleDegreeofFreedom (SDOF) System
A simplified model that represents a structure's dynamic behavior as if it has only one degree of freedom.
- Displacement Response Spectrum (S_d)
A spectral representation of the maximum displacement experienced by a structure relative to the ground motion.
- Velocity Response Spectrum (S_v)
A spectral representation of the maximum velocity experienced by a structure during ground motion.
- Acceleration Response Spectrum (S_a)
A spectral representation of the maximum acceleration experienced by a structure due to seismic forces.
Reference links
Supplementary resources to enhance your learning experience.
