Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding the SDOF System and Its Governing Equation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
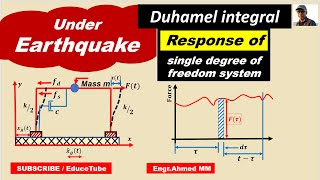
Today we're going to explore the Single-Degree-of-Freedom system and how it responds to seismic events. The dynamics of this system are described by the equation: m * ü(t) + c * u̇(t) + k * u(t) = -m * üg(t). Does anyone remember what each symbol in this equation represents?
I think **m** is the mass of the system, right?
Exactly! And what about **c** and **k**?
I believe **c** is the damping and **k** is the stiffness?
Correct! So with that, how would you define **u(t)**?
It’s the relative displacement of the system!
Great job! Remember, understanding the governing equation helps us predict how structures will perform during earthquakes.
Displacement, Velocity, and Acceleration Response Spectra
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand the governing equations, let’s discuss the response spectra: displacement, velocity, and acceleration. What do you think the significance of each type is?
I guess the displacement response spectrum shows how much a structure might move?
Right! It's crucial for figuring out how much deformation a building will experience. And how about the velocity response spectrum?
It probably relates to how fast the building is moving during an earthquake?
Exactly! And the acceleration response spectrum?
That's likely about how quickly the forces change, or how fast the acceleration is during shaking.
Excellent! These spectra help civil engineers design safer structures by predicting peak responses to ground motion.
Plotting and Application of Response Spectra
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
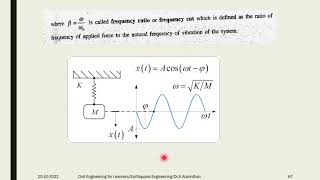
Finally, let’s talk about how we actually plot these response spectra. They are typically plotted against the natural period T or frequency ω of the system. Why do you think this is important?
It helps us see how different structures with various properties will behave in an earthquake?
Exactly! By comparing different spectra, engineers can assess which structures are more vulnerable to seismic activity. Do you remember some parameters we may vary to construct these spectra?
We can change the natural period and the damping ratio, right?
Correct! Keep in mind that the damping ratio can significantly influence the results we obtain from our response spectra.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The SDOF system plays a crucial role in earthquake engineering by providing insights into structural responses subjected to ground motion. The governing equation integrates parameters like mass, damping, and stiffness to determine various peak response parameters, leading to the construction of displacement, velocity, and acceleration response spectra.
Detailed
Single-Degree-of-Freedom (SDOF) System Response
The response spectrum is created based on the dynamic response of a Single-Degree-of-Freedom (SDOF) system when exposed to ground motion. The dynamics of such a system are governed by the equation:
$$ m \ddot{u}(t) + c \dot{u}(t) + k u(t) = -m \ddot{u_g}(t) $$
In this equation, u(t) represents the relative displacement of the system, ü(t) indicates the ground acceleration, while m, c, and k denote the mass, damping coefficient, and stiffness of the system, respectively.
Key response parameters include the displacement response spectrum S_d, velocity response spectrum S_v, and acceleration response spectrum S_a, all plotted against the natural period T or frequency ω of the system. Understanding these parameters is critical for engineers to assess the potential response of a structure during seismic events and for the development of effective design spectra.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to SDOF System Response
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A response spectrum is built from the dynamic response of an SDOF system subjected to a ground motion.
Detailed Explanation
The response spectrum is a mathematical representation that shows how a simple system, referred to as a Single-Degree-of-Freedom (SDOF) system, responds to ground motions caused by earthquakes. An SDOF system is a simplified model of a physical structure, such as a building or bridge, where we only consider its primary movement characteristics. The response spectrum helps engineers predict how various structures will behave during an earthquake, focusing on their peak movements.
Examples & Analogies
Think of a swing in a playground. When you push the swing (akin to ground motion during an earthquake), it moves back and forth (the swing's response). Engineers analyze how high the swing goes (peak response) based on how hard they push. The response spectrum is like a graph that shows how far the swing can go based on different push strengths, helping engineers understand how much a building might sway during earthquakes.
Governing Equation of SDOF Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Governing equation: mu¨(t)+cu˙(t)+ku(t)=−mu¨(t)g
where:
o u(t): Relative displacement
o u¨ (t): Ground acceleration
g
o m,c,k: Mass, damping, and stiffness
Detailed Explanation
The governing equation shown represents the dynamics of the SDOF system using terms that describe mass, damping, and stiffness. In this equation, 'm' represents the mass of the structure, 'c' represents the damping (how much energy is dissipated by the structure), and 'k' represents the stiffness (how resistant the structure is to deformation). The left side of the equation describes the forces acting on the system, while the right side accounts for the ground acceleration. Understanding this equation helps engineers determine how much a structure will move in response to seismic forces.
Examples & Analogies
Imagine a car going over a speed bump. The car's mass and suspension system will dictate how much the car bounces (relative displacement). The 'c' in the equation relates to the shock absorbers, which dampen the bounce, while 'k' relates to how stiff the vehicle's suspension is. Just as the car's behavior over the speed bump is predictable given its weight and suspension design, so too can engineers predict how a building will behave in an earthquake using this equation.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Governing Equation: Describes the dynamic behavior of the SDOF system under seismic loading.
-
Response Spectrum: A key tool in earthquake engineering to visualize structural responses.
-
Peak Response Parameters: Includes displacement, velocity, and acceleration spectra, crucial for understanding system performance during ground motion.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An SDOF system with a mass of 10 kg, damping ratio of 5%, and stiffness of 200 N/m can be analyzed to determine its response to earthquake-induced ground motion.
-
A bridge modeled as an SDOF system is subjected to a specific ground motion, producing distinct displacement, velocity, and acceleration responses.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In an SDOF, a peak we see, / Motion, speed, and force agree.
📖 Fascinating Stories
-
Imagine a swing at a playground, swaying back and forth. The height it reaches (displacement), how fast it goes (velocity), and the push it takes to swing (acceleration) illustrate an SDOF system in action.
🧠 Other Memory Gems
-
To remember the response spectrum parameters, think 'DVA': Displacement, Velocity, Acceleration.
🎯 Super Acronyms
Use 'SDOF' to remember
- Single-Degree-of-Freedom structure
- a: singular way to observe dynamic responses.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: SingleDegreeofFreedom (SDOF)
Definition:
A simplified structural model that describes dynamic behavior using a single coordinate, usually in terms of its displacement.
-
Term: Response Spectrum
Definition:
A graphical representation showing the peak response (displacement, velocity, or acceleration) of a structure for different natural periods and damping ratios.
-
Term: Damping Ratio (ζ)
Definition:
A measure of energy dissipation in a vibrating system, expressed as a fraction of critical damping.
-
Term: Natural Period (T)
Definition:
The time it takes for a system to complete one full cycle of vibration when disturbed.
-
Term: Ground Motion
Definition:
The motion of the ground due to seismic waves generated by an earthquake.