Construction of Response Spectra
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Time-History Analysis
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will discuss how to construct response spectra using time-history analysis. Who can tell me what time-history analysis involves?

Is it about evaluating how structures perform over time during seismic events?

Exactly! It's about simulating ground motions and assessing the structural response. We often use methods like the Newmark-beta method to integrate our calculations. Can anyone recall what it means to integrate numerically?

Is it about breaking down a complex problem into simpler parts for easier solving?

Great job! So, by using numerical integration, we can calculate peak responses such as displacement, velocity, and acceleration for an SDOF system. Remember, we vary the natural period and damping ratio to see how they affect the spectrum.
Normalization of Spectra
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we've covered time-history analysis, let's talk about normalization. Why do you think we normalize response spectra?

To make sure that the spectra can be compared against different ground motions?

That's right! Normalization allows us to scale spectra to a common reference. We can normalize using peak ground acceleration, velocity, or displacement. Can someone tell me why acceleration might be a preferred normalization point?

Because it relates directly to the forces acting on a structure?

Exactly! Using peak ground acceleration helps in relating the seismic forces to the response of the structure. It provides a valuable benchmark for design purposes.
Varying Natural Period and Damping Ratio
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Next, let's connect how varying the natural period and damping ratio impacts our response spectra. What do you think happens when we increase the damping ratio?

The spectral ordinates would likely decrease, right?

Correct! Higher damping levels reduce the peak response, which can be critical in ensuring safety. What about varying the natural period?

If we increase it, we might expect to see increased displacement responses?

Exactly! The natural period affects how we interpret the spectra, and understanding these relationships helps engineers design structures that can withstand seismic activity effectively.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
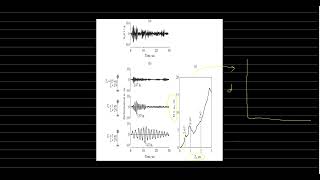
The construction of response spectra involves time-history analysis for SDOF systems, utilizing numerical integration methods for obtaining peak responses while varying natural periods and damping ratios. Normalization is also addressed, considering peak ground acceleration, velocity, and displacement.
Detailed
Construction of Response Spectra
In earthquake engineering, the construction of response spectra is crucial for analyzing how structures react to seismic activities. This section describes how to obtain response spectra through time-history analysis, where step-by-step numerical integration methods, such as the Newmark-beta method, are used to assess the peak responses of single-degree-of-freedom (SDOF) systems subjected to seismic ground motions. By varying the natural periods and damping ratios, engineers can create spectra that reflect different dynamic characteristics of structural systems. Additionally, normalization of the spectrum is discussed, with the options of peak ground acceleration (PGA), peak ground velocity (PGV), or peak ground displacement (PGD) serving as potential reference points. This normalization is vital in ensuring that the spectra are usable across various engineering and design contexts.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Time-History Analysis for SDOF Systems
Chapter 1 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- Step-by-step numerical integration (e.g., Newmark-beta method) is used to obtain peak responses.
- Spectra are constructed by varying the natural period and damping ratio.
Detailed Explanation
In this chunk, we learn about the process of constructing response spectra specifically for Single-Degree-of-Freedom (SDOF) systems. The first point mentions the use of time-history analysis, which involves applying a particular historical earthquake motion to the structure. The Newmark-beta method is a numerical integration technique that helps calculate how much the structure will move in response to that motion over time. By adjusting the parameters like the natural period (the time it takes the structure to complete one vibration cycle) and the damping ratio (how much the structure dissipates energy), we can generate a response spectrum that reflects the potential maximum responses (displacement, velocity, or acceleration) of the structure during an earthquake.
Examples & Analogies
Think of this process as tuning a musical instrument. Just as a musician adjusts the tension of the strings (natural period) and the way they dampen sounds (damping ratio) to achieve the perfect tone, engineers adjust these parameters to determine how their structures will react to seismic activities. The resulting response spectrum acts like the sheet music that tells them how the building will 'play' during an earthquake.
Normalization
Chapter 2 of 2
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
- The spectrum may be normalized by peak ground acceleration (PGA), peak ground velocity (PGV), or peak ground displacement (PGD).
Detailed Explanation
Normalization in the context of response spectra is an important step that allows engineers to compare the results from different responses or conditions more easily. By normalizing the spectrum, we scale the maximum responses to a standard reference point (like PGA, PGV, or PGD). This means that regardless of the specific ground motion used, the response can be presented in a uniform way. This normalization makes it simpler to assess how structures perform across different scenarios and helps in creating more generalized design spectra for use in engineering.
Examples & Analogies
Imagine a sports competition where athletes run races on different tracks. To fairly compare their times, each athlete's time is converted into a standard measure based on their performance compared to the fastest race (like the normalization process). This allows spectators to understand who runs the fastest relative to others, much like normalization in response spectra allows engineers to evaluate structural performance uniformly, regardless of varying conditions.
Key Concepts
-
Time-History Analysis: A method to evaluate the dynamic response of structures under seismic loads.
-
Single-Degree-of-Freedom (SDOF) System: A simplified model for analyzing structures as having one degree of motion.
-
Normalization: The process of scaling response spectra to a standard reference like peak ground acceleration.
Examples & Applications
An engineer uses the Newmark-beta method to analyze the peak acceleration of a bridge during an earthquake, resulting in a response spectrum that shows how the bridge will react over time.
After varying the damping ratio in a structural model, the engineer finds that increasing the damping reduces the expected maximum displacement response in the response spectrum.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In tremors deep, our structures quake, we analyze to not forsake.
Stories
Imagine a bridge caught in an earthquake's dance. Engineers study its movements, using time-history analysis to ensure it doesn't miss a chance to stand strong.
Memory Tools
N-D-C: Natural Period - Damping Ratio - Construction. Remember this for key aspects of response spectra.
Acronyms
S-PECTRUM
SDOF
Peak Ground Acceleration
Construction
Time-history
Response Understanding
Mechanism.
Flash Cards
Glossary
- TimeHistory Analysis
A method used to evaluate the response of structures subjected to time-dependent loads like seismic ground motions.
- SingleDegreeofFreedom (SDOF) System
A simplified model of a physical system, often used in structural dynamics, representing a structure's response as if it had only one degree of motion.
- Peak Ground Acceleration (PGA)
The maximum ground acceleration recorded during an earthquake, often used as a reference point for normalizing response spectra.
- NewmarkBeta Method
A numerical integration method used to analyze the dynamic response of structures subjected to time-varying loads.
- Natural Period
The time it takes for a structure to complete one full vibration cycle; crucial in determining its response to dynamic loads.
- Damping Ratio
A measure of how oscillations in a system decay after a disturbance; affects the response of structures during seismic events.
Reference links
Supplementary resources to enhance your learning experience.
