Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Foundation of Response Spectra
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's begin by discussing response spectra. Essentially, a response spectrum shows how structures react to seismic forces. Can anyone tell me what the response spectrum is built from?
Isn't it based on the dynamic response of single-degree-of-freedom systems?
Correct! The response spectrum is developed using the dynamic response of an SDOF system subjected to an earthquake. The governing equation is crucial, which combines mass, damping, and stiffness.
What does that equation look like?
It’s mu¨(t) + cu˙(t) + ku(t) = -mu¨(t)g, where each symbol represents aspects of the structure’s dynamics. Remember this as the mass-damping-stiffness relationship!
So all structures are treated as SDOF when analyzing them?
Not all, but it simplifies complex structures for preliminary assessments. Now let's summarize: response spectra are based on SDOF dynamics.
Peak Response Parameters
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Next, we have peak response parameters like displacement, velocity, and acceleration spectra. Can anyone explain why these are significant?
They help us know how much movement a structure can expect during an earthquake!
Exactly! Each is plotted against either the natural period T or frequency ω. To remember this, use the acronym 'DVA' for Displacement, Velocity, and Acceleration.
What’s each one beneficial for, though?
Good question! Displacement is crucial for aesthetic and operational concerns, velocity relates to impacts on non-structural components, and acceleration shows forces on the structure. Why would this distinction matter?
To design structures that are safe and functional under different types of seismic motion!
Exactly! Let's wrap up. The peak response parameters are critical for structural safety analysis.
Damping and Its Influence
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
We’ve talked about the components of response spectra, now let’s cover damping. What do you think happens to spectral ordinates as damping increases?
Wouldn’t they decrease because higher damping absorbs more energy?
Exactly! Higher damping leads to lower spectral ordinates. And did you notice how we usually consider common damping ratios like 2%, 5%, and 10%?
Why those specific percentages?
They are typical damping behaviors in various materials. Remember: Higher damping equals less response. Let's summarize the key point: damping significantly influences how structures respond during seismic events.
Elastic vs. Inelastic Response
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now we’ll discuss the difference between elastic and inelastic response spectra. Who can explain elastic response?
Isn't that when the structure behaves linearly?
Yes, it assumes linear behavior, which is typically used for initial design. Can anyone explain inelastic response?
That's when a structure can have plastic deformation, right?
Correct! Inelastic spectra use a modification factor to account for this. Now, to help you remember, think of 'E' for elastic 'L' for linear and 'I' for inelastic 'D' for deformation.
So the response modification factor is crucial during the design phase?
Absolutely! A solid understanding of both spectra types is essential for safety and sustainability in design.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section discusses the response spectrum, which illustrates peak structural responses to seismic ground motions, and the design spectrum, a modified version used in seismic design codes. Key concepts such as the construction of response spectra, the influence of damping, and the distinction between elastic and inelastic spectra are covered.
Detailed
Response and Design Spectra
In earthquake engineering, comprehending how structures react to dynamic loads, such as seismic ground motions, is vital. This section presents the response spectrum, a graph that shows the peak response in terms of displacement, velocity, or acceleration based on the natural period and damping ratio of structures. Alongside this, the design spectrum is introduced, adapted for implementation in seismic design codes ensuring structural safety.
Key Highlights:
- Fundamentals of Response Spectrum: Explanation of single-degree-of-freedom (SDOF) systems and the governing equations for their responses to seismic actions.
- Peak Response Parameters: Distinctions among displacement, velocity, and acceleration response spectra and their graphical representation against the natural period.
- Construction and Normalization: Details on the methods of constructing response spectra through time-history analysis and how spectra can be normalized based on peak ground acceleration, velocity, and displacement.
- Damping's Impact: Exploration of different damping ratios and their effect on spectral ordinates, along with the family of response spectra tailored for various damping levels.
- Elastic vs. Inelastic Responses: Clarification of the differences between elastic response spectra (assuming linear behavior) and inelastic spectra (considering plastic deformation with a response modification factor).
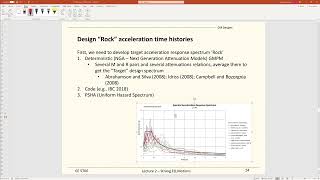
- Design Spectra Essentials: Necessity for design spectra in engineering, features of design spectra including the categorization by soil types, and code parameters such as zone factors, importance factors, and response reduction factors.
- Site Specificity and Soil Effects: Influence of local geological conditions on the spectra and the necessity of using site-specific measurements in certain structural designs.
- Applications in Structural Design: How design spectra are applied in calculating seismic loads, especially in linear dynamic analysis of high-rise and irregular structures.
- Comparative Analysis: A look at the limitations and assumptions of response spectra compared with time-history analysis; their respective complexities, accuracy, and use cases.
Failure to accurately model and apply these spectra can lead to under- or overengineering of structures, generating significant safety concerns.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Response Spectra
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the context of earthquake engineering, understanding how structures respond to dynamic loads such as seismic ground motions is essential. One of the most powerful tools for this purpose is the response spectrum, which provides a concise and effective means to represent the peak response (e.g., displacement, velocity, or acceleration) of a structure as a function of its dynamic properties, particularly the natural period and damping ratio. Complementing this, the design spectrum is a modified version of the response spectrum, tailored to be used in seismic design codes for ensuring structural safety and compliance. These spectra are indispensable in both linear and nonlinear dynamic analysis of structures subjected to earthquake ground motion. This chapter aims to explore the theoretical background, development, and practical application of response and design spectra in the seismic design and analysis of structures.
Detailed Explanation
This introduction sets the stage by explaining the importance of response spectra in earthquake engineering. It highlights how these spectra are used to assess how buildings will react to seismic activities, using critical parameters like displacement, velocity, and acceleration. It also explains that the design spectrum, a variation of the response spectrum, is utilized to ensure buildings meet safety standards during earthquakes.
Examples & Analogies
Think of a response spectrum like a weather forecast for buildings. Just as a weather report predicts the likelihood of rain, wind, or storms based on meteorological data, a response spectrum provides engineers predictions about how a building will react to seismic forces. Understanding this helps architects design safer buildings, much like choosing the right materials and techniques based on weather conditions.
Basic Concepts of Response Spectrum
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
33.1 Basic Concepts of Response Spectrum
33.1.1 Single-Degree-of-Freedom (SDOF) System Response
- A response spectrum is built from the dynamic response of an SDOF system subjected to a ground motion.
- Governing equation:
mu¨(t)+cu˙(t)+ku(t)=−mu¨(t) g where:
o u(t): Relative displacement
o u¨(t): Ground acceleration g
o m,c,k: Mass, damping, and stiffness
Detailed Explanation
This chunk introduces the basic components of the response spectrum theory, focusing on the Single-Degree-of-Freedom (SDOF) system. It explains that response spectra are derived using the dynamic responses of structures that can be simplified to a single mass moving in one direction. The governing equation outlines the physics involved in these systems, indicating how displacement, acceleration, mass, damping, and stiffness interact during seismic events.
Examples & Analogies
Imagine a pendulum swinging back and forth. In this analogy, the pendulum represents a structure, and how far it swings (its displacement) in response to an earthquake is similar to the dynamic response of buildings during seismic activity. The governing equation serves as a mathematical representation of how forces affect the pendulum's motion, helping engineers predict how different structures will respond to shaking.
Peak Response Parameters
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
33.1.2 Peak Response Parameters
- Displacement response spectrum S_d
- Velocity response spectrum S_v
- Acceleration response spectrum S_a
Each parameter is plotted against the natural period T or frequency ω of the system.
Detailed Explanation
This section details the types of response spectra: the displacement response spectrum indicates how much a structure will move, the velocity response spectrum shows how fast it will move, and the acceleration response spectrum measures how quickly the rate of change in speed occurs. These parameters are critical for assessing the performance and safety of structures during an earthquake, and they are plotted against the natural period or frequency of the structure, which helps engineers visualize the response characteristics.
Examples & Analogies
Consider driving a car. The speed (velocity) tells you how fast you're going, while how quickly you accelerate (acceleration) reflects how rapidly you change that speed. Similarly, in building design, understanding how much a building is likely to sway (displacement) and how quickly that swaying happens (velocity and acceleration) is vital for safety during an earthquake.
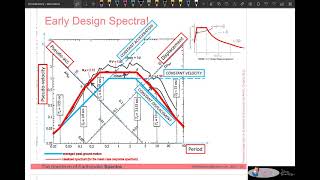
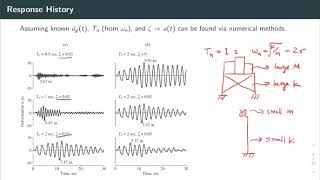
Construction of Response Spectra
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
33.2 Construction of Response Spectra
33.2.1 Time-History Analysis for SDOF Systems
- Step-by-step numerical integration (e.g., Newmark-beta method) is used to obtain peak responses.
- Spectra are constructed by varying the natural period and damping ratio.
Detailed Explanation
This chunk explains how response spectra are constructed through Time-History Analysis. Engineers use specific numerical integration methods (like Newmark-beta) to calculate how a structure will respond over time when subjected to ground motion. By varying parameters like the natural period (how long it takes for the structure to naturally oscillate) and the damping ratio (which measures how much energy is dissipated), engineers can create a detailed response spectrum for different scenarios.
Examples & Analogies
Creating a response spectrum is like training for a marathon. Just as a runner might vary their training regimen by adjusting distance and pace (natural period and damping), engineers adjust periods and damping values to simulate how buildings might behave under different earthquake conditions. This careful planning ensures that when 'race day' comes, the 'runner'—in this case, the building—is prepared to handle the stresses it will face.
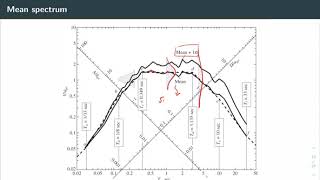
Normalization of Response Spectra
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
33.2.2 Normalization
- The spectrum may be normalized by peak ground acceleration (PGA), peak ground velocity (PGV), or peak ground displacement (PGD).
Detailed Explanation
Normalization refers to the process of adjusting the response spectrum based on specific reference points, such as Peak Ground Acceleration (PGA), Peak Ground Velocity (PGV), or Peak Ground Displacement (PGD). This standardization helps to create a more consistent framework for comparing different spectra, making it easier to analyze how structures might respond under various seismic conditions.
Examples & Analogies
Normalization is similar to using a common currency when comparing prices in different countries. Just as converting everything to a standard currency (like dollars) helps you understand costs more clearly, normalizing response spectra allows engineers to make meaningful comparisons between different scenarios of seismic activity, ensuring they can evaluate risk effectively.
Damping and its Influence on Spectra
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
33.3 Damping and its Influence on the Spectra
33.3.1 Damping Ratio (ζ)
- Common damping levels: 2%, 5%, 10%
- The higher the damping, the lower the spectral ordinates.
Detailed Explanation
This section delves into the concept of damping, which is a measure of how oscillations in a system decrease over time due to energy loss. Damping ratios, typically expressed as a percentage, indicate how responsive or resilient a structure is when faced with dynamic forces. Higher damping ratios result in lower spectral ordinates, meaning that structures with more damping tend to have less severe responses during an earthquake.
Examples & Analogies
Think of damping as the shock absorbers in a car. Just as good shock absorbers help smooth out the ride by absorbing some of the bumps in the road, higher damping in a building reduces the intensity of its swaying during an earthquake. This makes the structure safer and helps ensure that it can withstand seismic forces without significant damage.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Response Spectrum: Represents the peak response of a structure during seismic events.
-
Design Spectrum: A modulated response spectrum utilized in engineering design codes.
-
SDOF Systems: Simple models that represent structures with a single degree of freedom.
-
Damping Ratio: Indicates how quickly vibrations dissipate in a structure.
-
Elastic vs. Inelastic Response: Elastic assumes linear behavior while inelastic accounts for plastic deformation.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An SDOF system can be modeled to determine its response to a specific seismic input, allowing us to derive a response spectrum.
-
The design spectrum guides the design of buildings in earthquake-prone areas to ensure they withstand expected ground motions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Response spectra show how structures sway, in seismic waves, they find their way.
📖 Fascinating Stories
-
Imagine a bridge during an earthquake; a wise engineer uses the spectrum to gauge how much to shake and sway, ensuring the bridge holds strong at the end of the day.
🧠 Other Memory Gems
-
To remember the key aspects - DVA (Displacement, Velocity, Acceleration) for response parameters.
🎯 Super Acronyms
For damping, remember 'HLD' - Higher means Lower Displacement in spectral readings!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Response Spectrum
Definition:
A graph representing the peak response of a structure to seismic ground motions as a function of structural damping and period.
-
Term: Design Spectrum
Definition:
A modified response spectrum used in seismic design codes to ensure structural safety.
-
Term: SingleDegreeofFreedom (SDOF) System
Definition:
A simplified structural model that assumes the structure responds as a single mass with one degree of freedom.
-
Term: Damping Ratio (ζ)
Definition:
A measure of how oscillations in a system decay after a disturbance, typically expressed as a percentage.
-
Term: Elastic Spectrum
Definition:
A spectrum that assumes linear behavior of structures without accounting for any inelastic effects.
-
Term: Inelastic Spectrum
Definition:
A spectrum that accounts for plastic deformation in structures by utilizing a response modification factor.
-
Term: Peak Ground Acceleration (PGA)
Definition:
The maximum acceleration experienced by the ground during an earthquake.
-
Term: Response Modification Factor (R)
Definition:
A factor used in inelastic analysis to reduce the elastic demands based on ductility and redundancy.
-
Term: Natural Period (T)
Definition:
The time it takes for a structure to complete one full cycle of oscillation.