Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Mass Balance in Sediments
Unlock Audio Lesson
Today, we’re going to discuss mass balance in sediment systems. Can anyone tell me what mass balance means?
I think it's about how much material enters and leaves a specific volume or area?
Exactly! It's essentially keeping track of mass inputs versus outputs. In sediment systems, we're looking at rates that may change over time. What do you think that implies for pollution?
So if the input rates are high and outflows are low, pollution could accumulate?
Correct! This leads us to the non-steady state conditions we often observe. Let's remember: 'More in, less out = buildup of materials.'
Diffusion vs. Material Movement
Unlock Audio Lesson
Next, let’s talk about diffusion in sediment-water systems. How do you think diffusion differs from overall sediment movement?
Um, isn’t diffusion just how chemicals spread out in the fluid?
Yes, but it’s important to note that the overall accumulation of contaminants also involves material from the solid phase. Who can explain how this interplays with adsorption?
I think the solid phase collects materials as well, which can change the concentration gradients?
Exactly! This highlights the interactions between liquid and solid phases. Remember: 'Adsorption slows diffusion.'
Effective Diffusivity
Unlock Audio Lesson
Now, let’s explore effective diffusivity in porous media. Anyone want to share how porosity impacts diffusion?
More pores would mean there's more 'space' for materials to move, right?
Exactly! However, this also complicates the movements. We would also need to consider the 'tortuous paths'. Can someone explain what that means?
It's like when a person takes a winding path instead of a straight line. It takes longer!
Great analogy! The longer paths reduce effective diffusion. So, let’s summarize: 'Porosity increases pathways, but winding paths slow movement.'
Local Equilibrium Assumption
Unlock Audio Lesson
We have a simplification known as the local equilibrium assumption. Can anyone explain what it entails?
I think it means we assume that the different parts of the system are in equilibrium with one another?
Yes! It assumes that the adsorbed contaminants reach equilibrium quickly. However, this works best under specific conditions—can anyone think of a condition where this wouldn't hold?
If there's fast flow of water, right? That would change concentrations too quickly.
Exactly! Thus we say, 'Local equilibrium holds for slow interactions.'
Mathematical Framework and Retardation Factor
Unlock Audio Lesson
Finally, let’s look at the mathematical expressions that describe these dynamics, particularly focusing on the retardation factor. Any thoughts?
Isn’t that about how materials get slowed down in the process?
You’ve got it! It embodies how both the bulk density and adsorption influence diffusion rates, slowing it down. What can we think is critical for effective analysis?
Factor in all solid and liquid interactions and their concentrations?
Precisely! Summarizing, 'Retardation slows contaminant movement, influenced by solid-liquid dynamics.'
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the principles of mass balance within sediment systems, highlighting the non-steady-state conditions of accumulation and the mechanisms of diffusion affecting pollutants. It explains the significance of effective diffusivity in these systems and its relationship with factors like porosity and adsorption, providing insight into how contaminants behave in sediment-water interfaces.
Detailed
Environmental Quality: Monitoring and Analysis
This section addresses the intricate processes involved in monitoring environmental quality, specifically through analyzing the dynamics of sediments.
Key Concepts Covered:
- Mass Balance in Sediment: Starting with the foundational concept of mass balance, the professor introduces the formula representing the sediment volume. This foundational principle dictates how mass inputs and outputs interact to affect environmental conditions.
- Accumulation Dynamics: Unlike steady-state scenarios, the accumulation of materials in sediments can vary over time, indicating non-zero rates of change. The pros and cons of this non-steady state are discussed, emphasizing its implications for environmental monitoring.
- Diffusion Processes: A significant aspect mentioned is the role of diffusion in transporting materials into and out of the sediment system. The section highlights the difference between fluid-phase diffusion and overall material movement, stressing the importance of considering both in analyses.
- Effective Diffusivity: The concept of effective diffusivity addresses the challenges posed by porous media, illustrating how concentration gradients and material properties (like porosity) affect the rate of diffusion significantly.
- Local Equilibrium Assumption: The section introduces the local equilibrium assumption, whereby equilibrium at microscopic levels is assumed due to rapid adsorption and desorption rates relative to diffusion.
-
Mathematical Expression and Retardation Factor: A mathematical framework is presented, culminating in the introduction of retardation factors in diffusion equations. Here, the relationship between physical properties of materials and the rate of interaction with contaminants is articulated clearly.
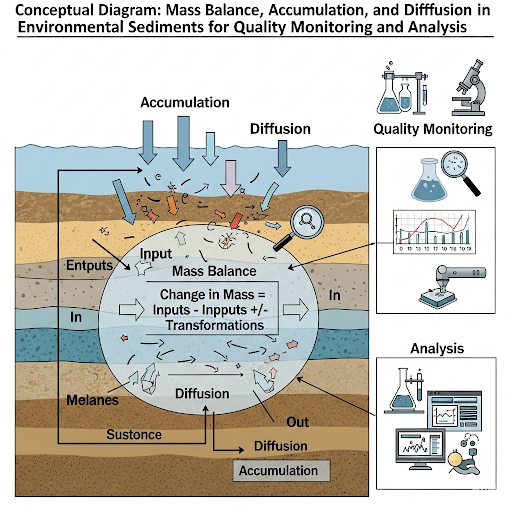
In summary, this section provides a foundational understanding of sediment behavior in environmental monitoring, emphasizing the need for careful consideration of mass transport phenomena.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Mass Balance in Sediments
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So what we are doing? We do this normally in all box models kind of scenarios. We write again the mass balance in the sediment volume. This is delta x, delta y, delta z is the differential volume of the system.
Detailed Explanation
In this chunk, we begin by discussing how we apply mass balance principles in sediment studies. The professor emphasizes the use of box models, which are simplified representations of a physical system. When we refer to 'delta x', 'delta y', and 'delta z', we are specifying the dimensions of a small volume within the sediment where calculations will be made. This small volume helps us analyze changes in concentration and material transport effectively.
Examples & Analogies
Imagine a large aquarium divided into sections where different variables like water quality are tested. Each section represents a 'box', and within each box, we can measure water levels, sediment concentrations, and other factors. This helps us analyze overall aquarium health, similar to assessing sediment in environmental studies.
Understanding Accumulation and Diffusion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, here I can write other terms if I want to, yeah, I can write many things. Same as box model, I can write whatever is happening inside the system. This is exactly what we did in box model except for two key differences. One is the rate of accumulation is now, it is nonzero, it is not steady state, something is not going out in the same manner.
Detailed Explanation
The second important point raised is about the accumulation in sediments not being steady-state. Here, accumulation refers to how contaminants are building up over time. Unlike a steady-state system where inputs equal outputs, in the case of sediments, the accumulation is dynamic, meaning that materials enter and leave at different rates. This showcases the complexity in tracking how substances disperse within sediment environments.
Examples & Analogies
Consider a sponge soaked in water. If you add more water while the sponge is still releasing some, the water level is dynamic; it's not always the same. This scenario is very similar to how contaminants accumulate in sediments where they can enter and exit at varied rates.
Diffusion in Sediments
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
What will you write in the rate in and rate out. So rate in and rate out is only by diffusion. This is only by diffusion, so which means it is a function of concentration gradients.
Detailed Explanation
Diffusion is explained as the primary mechanism for material transport in this scenario. The rates at which substances enter (rate in) and leave (rate out) the sediment are solely determined by diffusion, which is influenced by concentration differences. This principle states that materials will naturally move from areas of high concentration to low concentration until equilibrium is reached. It highlights how substances can migrate in sediments based on their environment.
Examples & Analogies
Think of how the smell of freshly baked cookies fills a room. The cookies release scent particles (high concentration) that spread throughout the air (moving to lower concentration) until you can smell them evenly across the entire space. This is similar to how contaminants diffuse through sediment particles.
Effective Diffusivity in Porous Medium
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is called as effective diffusivity in a porous medium and it is a function of the porosity of the system.
Detailed Explanation
In this section, the concept of effective diffusivity is introduced. Effective diffusivity is determined by how porous the medium (like sediment or soil) is. When a medium is filled with other materials (like solids in water), the paths available for diffusion become more complex. This means that diffusion occurs more slowly compared to a straightforward, unobstructed environment. Understanding effective diffusivity is crucial for predicting how quickly substances can move through sediments.
Examples & Analogies
Imagine trying to walk through a crowded room versus an open field. In the crowded room (porous medium), your movement is slower and more complicated due to obstacles (people). In contrast, the open field allows you to run freely (higher effective diffusivity). This analogy illustrates how effective diffusivity can be slower in environments with more obstacles.
Local Equilibrium Assumption
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This we will invoke what is called as a local equilibrium assumption. These are all simplifications for what could be the real scenario what is happening in the system.
Detailed Explanation
The local equilibrium assumption is a model simplification that assumes that the concentration of materials in the solid and fluid phases of the sediment equalizes quickly. This means that at every point, the levels of materials are balanced, making it easier to analyze the system. This assumption is particularly useful in modeling scenarios where adsorption and desorption are happening at similar rates to diffusion.
Examples & Analogies
Think of a perfectly balanced scale—if you add weight to one side, it immediately tips, but it quickly balances again as you redistribute the weight. This is similar to how local equilibrium assumes that concentrations quickly stabilize, allowing for straightforward modeling in systems where many interactions occur.
Conclusion and Further Considerations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We will see that tomorrow, how to solve this different, to solve it, you need boundary conditions and initial conditions.
Detailed Explanation
In the conclusion of this section, the professor indicates that the next steps will involve applying mathematical techniques to solve the diffusion equations in the context of environmental monitoring. This involves setting boundary and initial conditions—parameters that specify the behavior of a system over time and space, which is essential for accurately modeling environmental processes.
Examples & Analogies
Imagine setting rules for a game before you start playing; these rules will dictate how the game unfolds. Similarly, boundary conditions in environmental models help define how substances behave within the system, allowing for predictions and better understanding of environmental quality.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Balance in Sediment: Starting with the foundational concept of mass balance, the professor introduces the formula representing the sediment volume. This foundational principle dictates how mass inputs and outputs interact to affect environmental conditions.
-
Accumulation Dynamics: Unlike steady-state scenarios, the accumulation of materials in sediments can vary over time, indicating non-zero rates of change. The pros and cons of this non-steady state are discussed, emphasizing its implications for environmental monitoring.
-
Diffusion Processes: A significant aspect mentioned is the role of diffusion in transporting materials into and out of the sediment system. The section highlights the difference between fluid-phase diffusion and overall material movement, stressing the importance of considering both in analyses.
-
Effective Diffusivity: The concept of effective diffusivity addresses the challenges posed by porous media, illustrating how concentration gradients and material properties (like porosity) affect the rate of diffusion significantly.
-
Local Equilibrium Assumption: The section introduces the local equilibrium assumption, whereby equilibrium at microscopic levels is assumed due to rapid adsorption and desorption rates relative to diffusion.
-
Mathematical Expression and Retardation Factor: A mathematical framework is presented, culminating in the introduction of retardation factors in diffusion equations. Here, the relationship between physical properties of materials and the rate of interaction with contaminants is articulated clearly.
-
-
In summary, this section provides a foundational understanding of sediment behavior in environmental monitoring, emphasizing the need for careful consideration of mass transport phenomena.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The gradual increase of a pollutant in sediment layers can illustrate how mass balance reveals contamination over time.
-
Effective diffusivity can be demonstrated through experiments measuring how quickly ink spreads in a gel versus water.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In sediments where materials keep, watch the balance, don’t take a leap.
📖 Fascinating Stories
-
Once there was a lake that accumulated swans, but as they flocked, the balance felt the yawns. The more swans, the less fish, affecting nature's dish.
🧠 Other Memory Gems
-
DAVE: Diffusion Affects Volume Equally - remember diffusion’s effect on concentrations in sediment systems.
🎯 Super Acronyms
PATS
- Porosity Affects Transport Speed
- to remember how porosity impacts diffusion.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mass Balance
Definition:
A principle stating that the mass of a closed system must remain constant over time, accounting for mass inputs and outputs.
-
Term: Accumulation
Definition:
The rate at which materials build up in a system over time.
-
Term: Diffusion
Definition:
The process by which particles move from an area of higher concentration to an area of lower concentration.
-
Term: Effective Diffusivity
Definition:
A measure of how diffusion is affected by the structure of porous media and solid interactions.
-
Term: Retardation Factor
Definition:
A measure of how much a substance's movement is slowed down due to interactions with solids in porous media.
-
Term: Local Equilibrium Assumption
Definition:
An assumption that solid and liquid interactions reach equilibrium quickly enough to not be a limiting factor in analysis.