Retardation Factor
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mass Balance in Sediments
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today we'll start with the mass balance in sediment systems. Can anyone tell me what a mass balance means in this context?

I think it refers to how we account for all the materials present in the sediment.

Exactly! We look at the accumulation and interactions within the sediment volume. The mass balance equation helps us quantify changes.

Do we consider both solid and fluid phases in this balance?

Yes, indeed! Both phases are important because of the interactions that occur, including diffusion. Let's remember 'All Phases Matter' as a mnemonic for considering both solids and fluids!

What happens when there's a non-steady state?

Great question! In a non-steady state, the rates of accumulation and loss of substances vary, which requires us to model those changes over time more carefully. We'll explore that aspect in our next session.

Can you summarize that for us?

Of course! Remember that the mass balance in sediments considers both solid and fluid phases and that interactions, especially diffusion, can cause non-steady-state conditions.
Understanding Diffusion
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's dive into the diffusion aspect. Who remembers how diffusion impacts contaminant mobility?

It helps move pollutants from areas of high concentration to low concentration, right?

Exactly! But in sediments, we must consider the effective diffusion coefficient, DA3, which is influenced by porosity and solid mass. What do you think happens when porosity increases?

I guess the diffusion rate would improve since there's more space for the contaminants to move.

Correct! However, if the solid concentration is high, it can impinge on the diffusion rate. This interaction can be described as retardation. Who can summarize the relationship between porosity and diffusion?

'More Porosity, More Mobility!'

Excellent! Keep that mnemonic handy as we move into how the retardation factor comes into play.
Discussion on the Retardation Factor
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's talk about the retardation factor. How can we define it?

Is it the resistance that solids offer to the movement of contaminants?

Spot on! The retardation factor can be mathematically expressed as R = 1 + (rho � * Kd). Can anyone explain what rho � and Kd represent?

Rho � is the bulk density of the solids, and Kd is the distribution coefficient, which indicates how well a contaminant combines with a solid.

Perfect! So, if we have high Kd, does that mean diffusion will be faster or slower?

Slower, since it indicates more contamination sticking to the solid.

Exactly! And this is crucial in environmental monitoring. R is a vital parameter to include in our models. What's one key takeaway about R?

The greater R is, the slower the contaminant diffusion!

Well said! Understanding the retardation factor helps in predicting contaminant behaviors in sediment environments.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The retardation factor is a critical concept in environmental science that describes how solid materials in sediments can slow down the diffusion of contaminants. This section explains how the effective diffusion coefficient relates to properties such as porosity and solid mass, emphasizing the local equilibrium assumption and its role in modeling mass transfer in porous media.
Detailed
Retardation Factor
The retardation factor is an essential concept in environmental quality monitoring, particularly in understanding the diffusion of contaminants through sediment and water phases. In this section, we explore how the mass balance in sediment systems is affected by the interactions between fluids and solids, particularly focusing on mass diffusion.
Key Concepts
- Mass Balance in Sediments: In sediment volume, we analyze the mass balance equations to determine the accumulation and distribution of chemical substances. It is crucial to note that the rate of accumulation is dynamic and not steady-state as various factors such as diffusion and adsorption come into play.
- Role of Diffusion: Diffusion is a crucial mechanism for transport within the sediment-water interface. The movement of contaminants is governed primarily by diffusion, and understanding the mathematical representation of this process is vital for modeling environmental quality.
- Effective Diffusion Coefficient: The effective diffusion coefficient (DA3) illustrates how properties like porosity and bulk density influence the rate of diffusion in a porous medium. This factor is vital for understanding how easily substances move through sediment.
- Retardation Factor (R): The retardation factor is defined mathematically as R = 1 + (rho � * Kd), where rho � is the bulk density and Kd is the distribution coefficient. It highlights how the presence of solids can impede the diffusion of contaminants, making particle presence a significant barrier to transport.
-
Local Equilibrium Assumption: It is often assumed that in systems where solids and fluids interact, local equilibrium conditions make the rate of adsorption and desorption equal, facilitating easier calculation of contaminant concentrations over time.
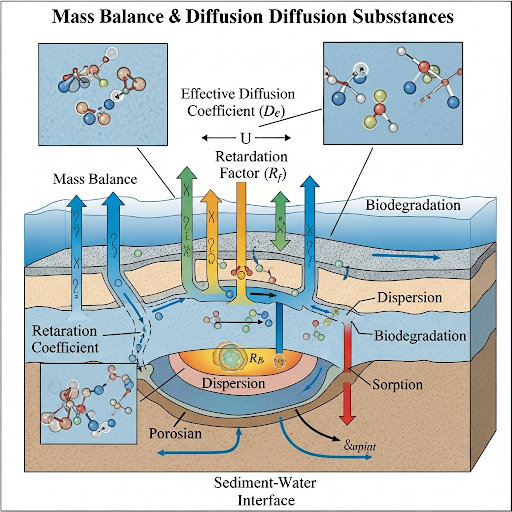
By understanding these concepts, students can appreciate how sediment characteristics influence environmental contaminant behavior and how this information can be applied in modeling and remediation efforts.
Youtube Videos










Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Effective Diffusion in Porous Media
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This is called as effective diffusivity in a porous media and it is a function of the porosity.
Detailed Explanation
Effective diffusivity refers to the rate at which substances diffuse through a porous medium, like soil or sediment. Unlike diffusion in free space, where substances move freely, in porous materials, the pathway is complicated due to the presence of solid particles. The presence of these particles affects how quickly substances can move through the material. Because diffusion occurs in the void spaces between particles, the porosity of the material heavily influences how quickly diffusion can happen. Higher porosity generally means more void space for diffusion, leading to higher effective diffusivity.
Examples & Analogies
Think about trying to walk through a crowded room (representing a porous medium). If the room is very crowded (low porosity), it takes a long time to reach the exit because you keep bumping into people (the solid particles). In contrast, in a very empty room (high porosity), you could move quickly and easily to the door because there are fewer obstacles in your way.
The Millington-Quirk Equation
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The effective diffusivity in a porous medium can be represented by the Millington-Quirk equation, which is given as DA = DA0 * (ϵ^4 / (1 - ϵ)^2) * (C), where C is a concentration related to the medium.
Detailed Explanation
The Millington-Quirk equation provides a mathematical relationship for calculating the effective diffusion coefficient (DA) in a porous material. In this equation, DA0 represents the diffusion coefficient of the substance in free space, ϵ stands for porosity (the fraction of the total volume that is void space), and C is a concentration term that accounts for the specifics of the material's composition. This equation highlights how porosity and the arrangement of solid particles affect diffusion rates.
Examples & Analogies
Imagine driving a car on a road that is sometimes narrow and sometimes wide. The narrower the road (representing lower porosity), the slower you can go because there is less space to move. Similarly, when substances move through a porous medium, their speed is affected by how much space (porosity) is available to them.
Retardation Factor Explained
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The term retardation factor, which is defined as R_f = (1 + (ρ_s * Kd) / ρ_w), where ρ_s is the bulk density of the solid, Kd is the partition coefficient, and ρ_w is the density of the fluid phase.
Detailed Explanation
The retardation factor (R_f) describes how much a contaminant's movement is slowed down in a porous medium because of its interaction with solid particles. A higher R_f indicates that the contaminant is more tightly bound to the solids and moves slower compared to how it would move in water alone. In essence, this factor combines the effects of bulk density (how much solid material is present) and the partition coefficient (how well the contaminant binds to the solid material), relative to the density of the fluid, to determine the overall speed reduction of a contaminant's movement.
Examples & Analogies
Consider a sponge (the porous medium) soaked in water (the fluid). If you try to squeeze out the water, it will take longer because the water is trapped in the tiny spaces of the sponge. Here, the sponge holds onto the water, slowing down its release. Similarly, the retardation factor explains how contaminants are held back by interaction with solid particles in soils or sediments.
Implications of Retardation in Environmental Engineering
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This retardation has significant implications for understanding contaminant transport in groundwater and sediment systems, affecting remediation strategies.
Detailed Explanation
The understanding of the retardation factor is crucial when designing systems to clean up contaminated sites. If contaminants bind strongly to sediment or soil, their movement is slowed down, which can have benefits or drawbacks. On the one hand, it might reduce the spread of the contaminant, giving remediation efforts more time to work. On the other hand, it might make it harder to remove the contaminant in a timely manner since it doesn’t move easily away from the solid matrix.
Examples & Analogies
Think of cleaning a spill on a carpet (the porous medium) versus cleaning up a spill on a smooth floor. On the carpet, the liquid is absorbed and held in place, making it harder to clean up quickly. Understanding how quickly or slowly it can be removed directly influences the cleanup strategy and time needed to restore the area.
Key Concepts
-
Mass Balance in Sediments: In sediment volume, we analyze the mass balance equations to determine the accumulation and distribution of chemical substances. It is crucial to note that the rate of accumulation is dynamic and not steady-state as various factors such as diffusion and adsorption come into play.
-
Role of Diffusion: Diffusion is a crucial mechanism for transport within the sediment-water interface. The movement of contaminants is governed primarily by diffusion, and understanding the mathematical representation of this process is vital for modeling environmental quality.
-
Effective Diffusion Coefficient: The effective diffusion coefficient (DA3) illustrates how properties like porosity and bulk density influence the rate of diffusion in a porous medium. This factor is vital for understanding how easily substances move through sediment.
-
Retardation Factor (R): The retardation factor is defined mathematically as R = 1 + (rho � * Kd), where rho � is the bulk density and Kd is the distribution coefficient. It highlights how the presence of solids can impede the diffusion of contaminants, making particle presence a significant barrier to transport.
-
Local Equilibrium Assumption: It is often assumed that in systems where solids and fluids interact, local equilibrium conditions make the rate of adsorption and desorption equal, facilitating easier calculation of contaminant concentrations over time.
-

-
By understanding these concepts, students can appreciate how sediment characteristics influence environmental contaminant behavior and how this information can be applied in modeling and remediation efforts.
Examples & Applications
If a pollutant diffuses through sediments with a high porosity, it moves faster. For instance, water contaminants in sandy soils diffuse quicker than in clayey soils due to higher porosity in sands.
Retardation factor R can shift based on chemical nature; highly adsorbing chemicals will have a larger R value, indicating slower movement through sediments.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
When solids are near, contaminants fear, for diffusion slows, that's crystal clear.
Stories
Imagine a crowded room; people can only move slowly among the obstacles. Similarly, in sediments, particles slow down contaminants just like the crowd hinders movement.
Memory Tools
P.E.R.F.E.C.T - Porosity, Equilibrium, Retardation, Flow, Effective diffusion, Concentration, Transport.
Acronyms
R = 1 + (rho � * Kd), where R is Retardation, rho is density, and Kd is the distribution coefficient.
Flash Cards
Glossary
- Retardation Factor (R)
A dimensionless number indicating the ratio of the time taken for a contaminant to move through a medium compared to the time it would take in a pure fluid.
- Effective Diffusion Coefficient (DA3)
The coefficient that adjusts the standard diffusion coefficient for the effects of pore structure and concentration gradients in a porous medium.
- Local Equilibrium Assumption
Assumption that the rate of adsorption is equal to the rate of desorption at any point in a system.
- Porosity
The fraction of void space in a material that can affect the movement of fluids and gases.
- Bulk Density
The mass of solids per unit volume of the sediment or soil, including the spaces between particles.
- Diffusion
The process through which molecules spread from areas of high concentration to areas of low concentration.
Reference links
Supplementary resources to enhance your learning experience.
