Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Mass Balance in Sediment Systems
Unlock Audio Lesson
Today's topic is mass balance in sediment systems. Can anyone tell me what mass balance means in this context?
I think mass balance refers to tracking the amount of chemicals within sediment and water, right?
Exactly! We often use a differential volume approach, defined as delta x, delta y, and delta z. This allows us to measure mass accumulation or loss over time.
But what happens if there’s a non-steady state? Does the equation change?
Great question! Yes, when we're not in steady state, we need to factor in the rate of accumulation, which is non-zero. We can express this in our equations.
So is it just diffusion that affects how chemicals move?
Yes! Diffusion is the main force at play, as we've mentioned. It drives chemicals from areas of high concentration to low.
Can you remind us how we would set up the equation for this?
Sure! The general equation for mass balance can be established, incorporating both influx and outflux concentrations based on diffusion rates.
In summary, mass balance is vital as it helps us quantify chemical concentrations in complex sediment and water systems.
Understanding Diffusion in Liquid Systems
Unlock Audio Lesson
Let’s delve into diffusion now! What do you understand about how diffusion operates in a porous medium?
I believe it's through the water in the pores, and that the path isn’t always straight because of the solids.
Correct! The movement through a porous medium creates a longer, tortuous path, effectively reducing the diffusion rate compared to a free liquid.
How can we quantify this effective diffusivity?
We use equations like Millington-Quirk's expression, which gives us a starting point to define effective diffusivity.
What assumptions do we make with that equation?
The assumption is that diffusion in the fluid and in the solid occurs uniformly, considering porosity impacts.
So higher porosity means faster diffusion?
Absolutely! Increased porosity typically allows for quicker diffusion rates due to the greater space available.
To summarize, diffusion in sediments is affected by both fluid and solid properties, significantly influencing mass transport.
Effective Diffusivity Formulae
Unlock Audio Lesson
In this session, we’ll review effective diffusivity equations, beginning with Millington-Quirk's expression. Does anyone remember it?
I think it's something like D_a = D_o ⋅ φ^4/3?
Close! It’s D_a = D_o ⋅ φ^4/3, where D_a is the effective diffusivity and D_o is the diffusivity in free liquid. Can anyone explain what porosity φ indicates here?
It indicates the relative volume of void spaces in the material, right?
Exactly! Higher porosity allows for better diffusion and vice versa. Are there any other equations you can think of about diffusivity?
You mentioned there are several, but I only remember this one.
Right. There are indeed other forms dependent on conditions such as saturation, and they are variations based on the scenario.
Could these changes affect our calculations in real-life scenarios?
Definitely! Accurate diffusivity impacts our predictions of contaminant transport and the effectiveness of remediation strategies.
To summarize, while Millington-Quirk's is common, understanding the underlying assumptions is just as crucial.
Exploring the Local Equilibrium Assumption
Unlock Audio Lesson
Next, let’s discuss the local equilibrium assumption. What does this term suggest?
I think it assumes that the solid and liquid phases reach equilibrium quickly?
Right! It assumes that diffusion rates and adsorption processes are comparable, leading to a quick equilibrium at each point.
So, it allows us to define relationships between the solid and liquid concentrations?
Exactly! This leads to equations such as C_A = K_d ⋅ C_star, promoting easier calculations for concentration relationships.
But what if flow is involved? Does that change things?
Absolutely. If there's significant flow, the rates will differ, and local equilibrium may not hold anymore.
How do we know when to apply this assumption then?
You apply it when diffusion dominates, especially in scenarios where water isn’t flowing rapidly. It's a simplification but useful.
In summary, understanding local equilibrium helps in modeling the interactions within saturated sediments effectively.
Solving the Differential Equations
Unlock Audio Lesson
Finally, let's go over how we solve our mass balance equations using differential equations!
I understand we need initial and boundary conditions, but how do they work?
Great! The initial conditions represent the state at the start, while boundary conditions are required to limit the problem space. They guide the solutions.
So if we set up the conditions correctly, we can find concentration over time?
Yes, exactly! After structuring the equations, we'll analyze and derive the concentration profile.
What happens if we don't set these conditions accurately?
Incorrect conditions lead to misleading results, hence careful consideration is vital!
Can you walk us through a brief example of this?
Certainly! Consider a hypothetical sediment system. We'd define initial contaminant concentration and establish where and how the contamination is spreading.
To sum up, solving these equations provides valuable insights into the kinetics of mass transport in sediment environments.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the interplay between liquid and solid phases in sediment systems is examined through mass balance equations. Key concepts include the rate of accumulation in non-steady states, the effective diffusion coefficient, and the impact of porosity on diffusion rates. The section emphasizes the importance of understanding these dynamics for environmental monitoring and analysis.
Detailed
Detailed Summary
The section provides a comprehensive overview of the equations describing the mass balance for chemical substances within liquid systems, particularly in the context of sediment-water interactions. It begins by establishing a differential volume approach using the terms of mass accumulation, defining diffusion parameters, and addressing the complexities introduced by both solid and liquid phases.
- Mass Balance Approach: The professor outlines how to formulate mass balance equations in a sediment volume, drawing parallels with box model scenarios but recognizing nuances such as non-steady states and rate of accumulation.
- Diffusion Dynamics: The process of diffusion across the sediment-water interface is discussed, highlighting that diffusion is the primary mechanism for mass transfer. The equations are derived to reflect this transfer, incorporating the roles of concentration gradients in both the liquid and solid mediums.
- Effective Diffusivity: A significant focus is given to the concept of effective diffusivity in porous media, illustrating how internal porosity affects the rate of diffusion. Various equations, including Millington-Quirk's expression, are presented as foundational models for diffusion in soil and sediment systems.
- Local Equilibrium Assumption: The section introduces the local equilibrium assumption, a simplification where adsorption and diffusion are assumed to occur at similar rates, allowing for a linear relationship in concentration terms. This assumption is pivotal for formulating the equations that relate the solid-phase concentration to that of the liquid phase.
- Application of Derived Equations: Conclusively, the derived equations are set as partial differential equations that require initial and boundary conditions for solving. The relevance of these mathematical models for understanding contaminant transport in aquatic environments is stressed.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Mass Balance in Sediment Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
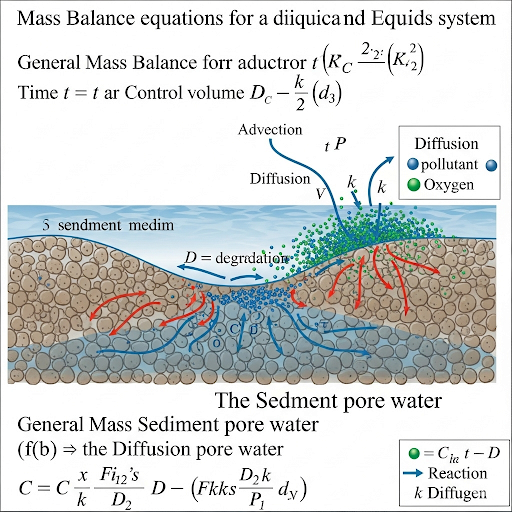
So what we are doing? We do this normally in all box models kind of scenarios. We write again the mass balance in the sediment volume. This is delta x, delta y, delta z is the differential volume of the system.
Detailed Explanation
In this chunk, the concept of mass balance within a sediment volume is introduced. It refers to tracking all the incoming and outgoing mass from a defined volume element (delta x, delta y, delta z) of sediment. The parameters delta x, delta y, and delta z represent small sections in three-dimensional space, indicating that the mass balance is applied to a tiny cube of sediment.
Examples & Analogies
Think of a fish tank as the sediment volume. If you add fish (mass in), remove some fish (mass out), and water evaporates (also mass out), you can apply a mass balance to understand how many fish and how much water remain in the tank.
Rate of Accumulation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, here I can write other terms if I want to, yeah, I can write many things. Same as box model, I can write whatever is happening inside the system. This is exactly what we did in box model except for two key differences. One is rate of accumulation is now, it is nonzero, it is not steady state, something is not going out in the same manner.
Detailed Explanation
The professor points out that in typical box model scenarios, the rate of accumulation might be zero, indicating a steady state. However, in the case of chemical mass in a liquid system, the rate of accumulation becomes non-zero. This implies that the system is not in steady state, as more mass is entering or accumulating than leaving, resulting in changes over time.
Examples & Analogies
Consider a sponge soaking up water. Initially, it might be dry and as water is added (rate of accumulation), it becomes saturated (not steady state). Once full, it will no longer absorb more water, reaching steady state when the rate in equals the rate out.
Diffusion as the Mode of Transport
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
What will you write in the rate in and rate out. So rate in and rate out is only by diffusion. This is only by diffusion, so which means it is a certain formula related to diffusion.
Detailed Explanation
This part emphasizes that the only process affecting the mass transfer in and out of the sediment volume is diffusion. Diffusion is the natural movement of particles from an area of higher concentration to an area of lower concentration. The professor further specifies that this process can be mathematically expressed using certain diffusion equations.
Examples & Analogies
Imagine placing a drop of food coloring in a glass of water. Over time, you will see the color spread throughout the water due to diffusion, moving from a concentrated area (the drop) to a less concentrated area (the surrounding water).
Effective Diffusivity in Porous Media
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This term here therefore reduces the effective diffusion of a material across a porous medium okay. This is the simple explanation, this is called as effective diffusivity in a porous media and it is a function of the porosity.
Detailed Explanation
Effective diffusivity refers to how diffusion is impacted by the structure of the medium through which substances are diffusing, particularly in porous materials. The porosity, or the amount of empty space in the medium, directly affects how easily substances can diffuse through it. The more complex the medium's structure, the lower the effective diffusivity.
Examples & Analogies
Consider walking through a field of tall grass versus walking on a paved path. It's much easier and quicker to move across the pavement (higher effective diffusivity), while the grass makes movement slower and more complicated due to the obstacles (lower effective diffusivity).
General Equation for Diffusion Coefficients
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A very commonly used expression is DA3 = DA . (porosity)^4/3 which is called as Millington Quirk’s expression.
Detailed Explanation
This is an equation used to calculate diffusion coefficients in porous media, suggesting that the effective diffusivity decreases with increasing porosity. Millington Quirk's expression is a simplified way to model how diffusion coefficients behave based on the structural properties of the material.
Examples & Analogies
Think of diffusion through a crowded room (like high porosity), where moving around is slow compared to a clear corridor (low porosity). The formula captures how the 'crowd' can affect movement, just as porosity affects diffusion.
Local Equilibrium Assumption
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This we will invoke what is called as a local equilibrium assumption. ... Therefore, if that is happening, then we cannot have local equilibrium assumption.
Detailed Explanation
The local equilibrium assumption posits that in a system where diffusion occurs, the rates of adsorption and desorption reach an equilibrium at local sites in a very short time frame. If the rate of movement (or flow) of the liquid is rapid compared to the rates of adsorption/desorption, this assumption breaks down, suggesting a more complicated interaction.
Examples & Analogies
Imagine a crowded elevator where all people must wait until it fills (adsorption) before they can leave (desorption). However, if a new group rapidly enters (fast flow), there may not be enough time for everyone to adjust, breaking the equilibrium.
Retardation Factor
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If the chemical is highly adsorbing, the partition constant is very big, very large, if the partition constant is large, it reduces the magnitude of diffusion, it retards diffusion.
Detailed Explanation
The retardation factor illustrates how adsorption impacts the diffusion process. High levels of adsorption mean that chemicals are held back and diffusion slows down. The retardation factor is a ratio that shows how much the presence of adsorbents slows down the transport of chemicals in the system.
Examples & Analogies
Think about a sponge soaking up water. If it’s fully saturated (high adsorption), even if you pour more water on it (high concentration), it won’t absorb more water quickly. The sponge ‘retards’ the water from moving through, similar to how adsorbents retain chemicals.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Balance: A crucial concept for tracking chemical amounts in sediment systems.
-
Diffusion: The primary mechanism for transporting chemicals in liquid systems.
-
Effective Diffusivity: Adjusted coefficient accounting for the porous nature of sediment materials.
-
Local Equilibrium: Assumption that enables simpler calculations based on the equilibrium of concentration between phases.
-
Porosity: Indicates the space available for fluids within a solid structure affecting diffusion rates.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of mass balance could be applied in tracking contaminant levels in a pond sediment.
-
In agricultural soil, diffusion principles help in predicting nutrient movement.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To know mass balance, count it clear, In and out, year by year.
📖 Fascinating Stories
-
Imagine a pond where fish live and swim. Each day they eat and some swim out; we need to count them to know how many are left—this is like mass balance in nature.
🧠 Other Memory Gems
-
To remember the steps of effective diffusivity: DED—Diffusion, Environment, Density (D_A = D_o × φ^4/3).
🎯 Super Acronyms
P.E.A.C.E
- Porosity
- Effective diffusivity
- Adsorption
- Concentration
- Equilibrium for sediment systems.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mass Balance
Definition:
An accounting of the mass entering and exiting a system over time.
-
Term: Diffusion
Definition:
The process by which molecules move from an area of high concentration to an area of low concentration.
-
Term: Effective Diffusivity
Definition:
A modified diffusion coefficient that accounts for the geometry and properties of a porous medium.
-
Term: Local Equilibrium Assumption
Definition:
An assumption that solid and liquid phases reach equilibrium quickly, allowing simplifications in calculations.
-
Term: Porosity (φ)
Definition:
The ratio of the volume of voids to the total volume, reflecting the pore space in solids.