Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Linear Momentum Conservation
Unlock Audio Lesson
Today, we will explore the concept of linear momentum conservation in fluid mechanics. Can anyone tell me why this concept is crucial in engineering applications?
Because it helps us analyze how fluids behave under different forces, right?
Exactly! Linear momentum conservation deals with how the motion of fluid particles is influenced by external forces. Can anyone name some of these external forces?
Body forces such as gravity!
And surface forces like pressure, correct?
Spot on! To remember these types of forces, think of 'Body = Gravity' and 'Surface = Pressure.' Let's move ahead and discuss how we can apply these concepts.
Reynolds Transport Theorem and Control Volumes
Unlock Audio Lesson
Let's delve into the Reynolds transport theorem. Who can tell me how it relates to control volumes?
It helps us analyze mass and momentum transfer through a defined volume, right?
Correct! The control volume framework allows us to simplify complex real-world scenarios into manageable equations. Could anyone explain the difference between fixed and moving control volumes?
A fixed control volume doesn't change position while a moving control volume follows the fluid motion.
Excellent! Remember: 'Fixed is static; move is dynamic.' Now, let’s see how we apply this to our equations for steady flows.
Applications of Linear Momentum Equations
Unlock Audio Lesson
Now that we understand the theory, let’s talk applications! What engineering scenarios might we use linear momentum equations for?
To calculate forces on structures like bridges when water flows past them!
Also for jet experiments in labs!
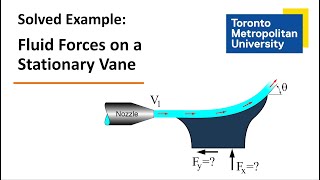
Exactly! In these scenarios, we can determine force components based on the momentum flux through the control volumes. We need to be aware of corrections for non-uniform flow. Who can explain what momentum flux correction factors are?
They account for variations in velocity distribution across a cross-section of a flow!
Right again! Remember: 'Correction Equals Perception!' Let’s apply this understanding to a problem.
Real-World Impacts: CFD and Pressure Distributions
Unlock Audio Lesson
Let’s talk about modern engineering techniques, specifically Computational Fluid Dynamics (CFD). How does CFD help us in analyzing pressure around structures?
It allows us to visualize complex flows in 3D, showing how pressure changes around structures!
Exactly! These visualizations can mitigate issues in design by predicting how a structure interacts with fluid flow. What’s one challenge we face in non-steady flow systems?
Turbulence!
Right! Turbulence introduces uncertainties in our momentum calculations. We need to account for these as we approach real-world applications.
Summary and Key Points
Unlock Audio Lesson
Let’s summarize what we’ve learned today. What are the key points about external forces in linear momentum?
We discussed body and surface forces and their applications!
And how to apply the Reynolds transport theorem to control volumes!
Excellent recall! We see linear momentum is crucial for calculating forces in fluid systems. Remember, integrating this understanding will improve our engineering designs. Great work today, everyone!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section highlights the importance of linear momentum conservation in fluid mechanics, detailing the effects of body and surface forces on control volumes, the simplification of equations under various conditions, and how these principles are applied in engineering scenarios such as pressure distributions and force calculation.
Detailed
Detailed Summary
The conservation of linear momentum is a fundamental concept in fluid mechanics, serving as the basis for analyzing fluid flows subjected to external forces. In this section, we focus on the Reynolds transport theorem and its application to control volumes, specifically differentiating between fixed and moving control volumes. The lecture discusses two main types of forces acting on control volumes:
- Body Forces: Predominantly gravitational forces.
- Surface Forces: Including pressure and reaction forces.
The discussion progresses into the application of linear momentum equations to engineering problems, highlighting how to derive force components when accounting for velocity and pressure distributions. A significant aspect of flow dynamics is identified—the momentum flux correction factors necessary for non-uniform velocity distributions.
This section draws attention to scenarios with steady flows across control volumes, emphasizing the critical equations governing mass influx and outflux, and how they hinge upon conservation principles. The practical implications of these theories are presented through examples, such as jet experiments and visualizations of flow patterns around structures like bridge piers, demonstrating the importance of computational fluid dynamics (CFD) in modern analysis.
The use of integral concepts enables simplifications in scenarios involving one inlet and one outlet, allowing for direct applications of momentum equations to yield force components without exhaustive derivations each time. This section is integral to understanding how fluid mechanics principles apply to real-world problems, providing a framework that balances mathematical rigor with explanatory illustrations.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Control Volumes in Fluid Mechanics
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come to today's lecture, we will have a steady flow across missions for the linear momentum equations. Many of the times, we have a linear momentum equations we solve for the one inlet or one outlet and in one directions and some of the problems we have solved with no external forces, then how the momentum equations can be simplified.
Detailed Explanation
In fluid mechanics, control volumes are critical to analyze fluid flow. A control volume is a defined space through which fluid flows. In today's lecture, we're specifically examining scenarios with one inlet and one outlet, simplifying linear momentum equations. We consider cases where external forces, such as gravity or pressure, do not affect the flow to understand fundamental concepts better.
Examples & Analogies
Imagine a garden hose with water flowing through it. If you observe the hose at a section where there's only one inlet (where the water comes in) and one outlet (where the water exits), you can apply the linear momentum equations easily. Without considering external forces, you can simplify your observations to understand how pressure and velocity will behave at these two points.
Forces on a Control Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
There will be two types of forces, body forces and the surface forces. The surface forces are pressures and the reactions forces, that what we talked a lot. Discuss also today body forces mostly what the problems we can consider is only the gravity force we consider as a body force, not the electric magnetic forces.
Detailed Explanation
When analyzing fluids in a control volume, we identify two main categories of forces: body forces and surface forces. Body forces act throughout the volume of the fluid, such as gravitational forces. Surface forces, on the other hand, act on the boundaries of the control volume, primarily due to pressure exerted by the fluid itself. For our discussions, we mainly focus on gravitational forces as the typical example of body force.
Examples & Analogies
Think of a swimming pool. The water itself exerts pressure on the walls and bottom, which represents surface forces. However, the gravitational pull that keeps the water in the pool is a body force. Both of these forces affect how the water moves and behaves inside the pool, just like how they affect fluids in a control volume.
Momentum Flux Correction Factors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Then, we also discussed about the momentum flux correction factors, this is a very simplified concept used to determine the momentum flux passing through a non-uniform cross-section.
Detailed Explanation
Momentum flux correction factors are adjustments made when calculating momentum flux in areas where the velocity of fluid is not uniform across a section. In simpler terms, if the fluid doesn’t flow evenly — for instance, faster in the center and slower near the edges — the correction factor helps account for this variation in speed. This correction ensures more accurate predictions of momentum behavior in various situations.
Examples & Analogies
Consider a river with varying widths. In a narrow section, the water flows quickly compared to a wider section where it flows slowly. If you want to calculate the total force of the water, you would need to adjust your calculations to reflect the differing speeds across the width of the river. The momentum flux correction factors allow you to do just that - they help ensure that the flow variations are accurately captured in calculations.
Solving for Steady Flow Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, go for a simple problems, where you have a linear momentum equations like you have a fixed control volume.
Detailed Explanation
In this section, we focus on how to apply linear momentum equations to steady flow scenarios. A fixed control volume helps to illustrate how fluid behaves under consistent conditions, examining variables such as momentum inflow and outflow. By fixing the control volume, we can simplify the equations as changes over time are held constant, allowing us to analyze the forces at play more easily.
Examples & Analogies
Think of a water tank that is continuously filled and drained at constant rates. Because the water levels stabilize, you can analyze the movement of water by focusing on the rates at which it flows in and out without worrying about sudden changes. This is akin to our control volume analysis, where we can focus on steady conditions and develop straightforward equations.
Applying Linear Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The net momentum flux will be the positive and incoming momentum flux will be the negative. So, the rate of change of this net out flux of this momentum flux will be the force component.
Detailed Explanation
Understanding the net momentum flux is crucial when applying the linear momentum equations. Typically, we define outgoing momentum flux as positive and incoming as negative, establishing a clear convention. The difference between these values gives us the net momentum change, which directly relates to the forces acting on the control volume.
Examples & Analogies
If you have two fans blowing air into a room, the amount of air entering (which can be viewed as incoming momentum flux) can be seen as negative if the exiting air through an open window is positive. The balance, or difference, between the incoming and outgoing air represents a change in momentum that results in various forces felt inside the room, similar to the forces applied in our control volume analysis.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Conservation of Linear Momentum: Essential for analyzing the motion of fluids affected by external forces.
-
Reynolds Transport Theorem: A crucial tool for simplifying fluid dynamics problems by connecting control volumes to flux rates.
-
Types of Forces: Body forces (like gravity) and surface forces (like pressure forces) have distinct impacts on fluid dynamics.
-
Momentum Flux: Indicates the distribution and flow of momentum across control surfaces within control volumes, critical for pressure calculations.
-
Momentum Flux Correction Factors: Account for variations in velocity distributions in real-world applications.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Analyzing the forces on a bridge pier when water flows past it involves understanding both momentum and pressure distributions.
-
In a jet experiment, momentum flux is crucial to determine the impact and force exerted by a jet of fluid.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Momentum flows in straight lines, under forces it will shine.
📖 Fascinating Stories
-
Imagine a river with water flowing smoothly past a bridge. The pressure it exerts on the bridge piers illustrates the concept of momentum and allows us to calculate forces acting on structures.
🧠 Other Memory Gems
-
Remember: 'C-MF' for Control-Momentum Flux! They are all intertwined in flow analysis.
🎯 Super Acronyms
B-S-F, for Body, Surface Forces - the critical players in fluid momentum!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Linear Momentum
Definition:
Momentum that is directed in a straight line, defined as the product of mass and velocity.
-
Term: Reynolds Transport Theorem
Definition:
A theorem that relates the change of quantity within a control volume to the flux of that quantity across the control surface.
-
Term: Control Volume
Definition:
A specified volume in space through which fluid flows, allowing for the analysis of mass, momentum, and energy transfers.
-
Term: Body Forces
Definition:
Forces that act throughout the entire volume of a fluid, such as gravity.
-
Term: Surface Forces
Definition:
Forces acting at the surface of a fluid element, often resulting from pressure or viscous effects.
-
Term: Momentum Flux
Definition:
The rate at which momentum passes through a unit area of a control volume.
-
Term: Momentum Flux Correction Factor
Definition:
A correction applied to account for non-uniform velocity distributions when calculating momentum flux.