Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Simplifications in Steady Flow
Unlock Audio Lesson
Welcome to today's session! Let’s dive into the concept of simplifications in steady flow. Who can tell me what they understand by the conservation of momentum?
Isn't it about how momentum isn't lost in a closed system?
Exactly, great answer! Momentum conservation states that the total momentum in a closed system remains constant. In fluid mechanics, we often simplify equations to focus on steady-state flows. Why do we do this?
To make calculations easier, right?
Yes! By simplifying, we can analyze complex flows more efficiently. Remember, acronyms help—you can memorize simplification as 'FAST': Fixed control volume, Analytical approach, Steady assumption, and Total momentum.
That’s handy! Is there a reason we focus on steady flows specifically?
Good question! Steady flow means the fluid properties at a point do not change over time. This allows us to use simplifications such as neglecting time derivatives in our equations.
What types of forces do we consider?
We primarily consider body forces like gravity and surface forces like pressure. Let’s move on to see how we apply these principles.
Control Volume Analysis
Unlock Audio Lesson
Now that we understand steady flow, let's discuss control volumes! Can anyone explain what a control volume is?
It's a defined volume in which we analyze the fluid movement, right?
Correct! We analyze fluid movement across the boundaries of this volume. If we have multiple inlets and outlets, how do we compute the forces acting on it?
We sum the momentum fluxes in and out, accounting for force components.
Precisely, well done! Let's classify some examples of steady flows in control volumes. If I have a pipe with water flowing in, what inputs do I need to consider?
We need the inlet velocity and pressure, and also the outlet conditions.
Exactly! And remember the 'Q1 = Q2' principle from the conservation of mass helps us in calculating the flow rates. Does anyone recall how we represented these quantities mathematically?
Using the equation of continuity!
Very good! So summarizing, in control volumes we meticulously analyze inflows and outflows to assess the forces acting. Let’s apply this understanding with some examples next.
Application of Momentum Flux Correction Factors
Unlock Audio Lesson
Let’s pivot to momentum flux correction factors. Can anyone share why these are necessary in our calculations?
They account for variations in velocity across a cross-section?
Exactly! In real-world applications, the velocity isn't uniform. Can someone give an example of where we might encounter this?
In pipes with changing diameters, for instance!
Correct again! In such cases, how might we calculate the momentum changes?
By using the corrected average velocities in our equations?
Yes! 'Beta' is the term we use for the correction factor. It's crucial for accurate results in engineering applications. For practice, why not jot down how you would calculate these values?
I’ll make sure to include the areas over which the velocities are measured!
Perfect! So always remember to consider variations and apply correction factors for accuracy.
Summary and Tips for Applying Momentum Equations
Unlock Audio Lesson
As we approach the end of today’s session, let’s summarize the key tips for applying momentum equations. What do you think the most important aspect is?
Using the right control volume and recognizing vector components!
Absolutely! Also, can anyone recall how to ensure correct sign conventions for momentum flux?
By analyzing the angles between velocity and normal vectors to surfaces, right?
Well remembered! This is vital because it prevents miscalculations. Linearity in equations, and recognizing when we can ignore terms due to steady-state conditions are also key points. Now for a fun memory aid, let's think of 'MUSE': Momentum, Uniform flow, Steady-state, Equilibrium.
That's a clever way to remember it!
Indeed! So, any final questions before we wrap up?
No, I think I've got a solid grasp on it now!
Great! Remember, practice makes perfect! Keep exploring these concepts!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The key point of this section is to show how momentum equations can be simplified when analyzing fluid motion in steady flow situations, focusing on their applications in engineering scenarios, such as force and velocity calculations. Key simplifications include discussing one inlet and outlet systems while emphasizing control volume methodologies.
Detailed
Detailed Summary
In fluid mechanics, particularly in the study of steady flows, simplifying the equations governing momentum conservation can greatly enhance problem-solving efficiency. This section elaborates on these simplifications, specifically utilizing Reynolds transport theorems combined with control volume concepts. The essence of the simplifications lies in analyzing systems with specific inlet and outlet conditions, wherein external forces may be absent, allowing for the streamlined application of momentum equations.
Key Points:
- Control Volumes: A fixed control volume approach is essential for analyzing systems with steady inflow and outflow.
- Momentum Flux and Body Forces: The contribution of body forces, usually gravity, and surface forces are considered, simplifying the forces acting on the control volume.
- Momentum Flux Correction Factors: These factors account for non-uniform velocity distributions across a cross-section, making them crucial for accuracy in engineering applications.
- Examples and Applications: Practical examples, including jet experiments, reinforce the theoretical underpinnings and demonstrate their applications in real-world scenarios.
- Hints & Tips: Several strategies are provided to effectively apply linear momentum equations, emphasizing vector components and constant pressure conditions in subsonic flows.
Overall, this section lays the groundwork for understanding how simplifications in steady flow lead to effective analyses and solutions in fluid dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Simplifications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come to today's lecture, will have a steady flow across missions for the linear momentum equations. Many of the times, we have a linear momentum equations we solve for one inlet or one outlet and in one directions and some of the problems we have solved with no external forces, then how the momentum equations can be simplified.
Detailed Explanation
This chunk introduces the topic of simplifying linear momentum equations, specifically in scenarios with steady flow. The focus is on conditions with one inlet and one outlet, where the external forces are negligible or absent. Simplifying these equations helps us understand fluid behavior more easily.
Examples & Analogies
Think of it like calculating how water flows through a single pipe with one opening: by simplifying our calculations, we can easily determine how quickly the water moves without considering complex factors like varying pressure or friction.
Equations for Steady Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Then fourth what we will talk about, when you apply the linear momentum equations, what are the hints and tips, what should we consider when you apply that linear momentum equations.
Detailed Explanation
In this chunk, the lecturer discusses the importance of hints and tips while applying linear momentum equations in steady flow situations. These considerations help in ensuring that the application of these equations yields accurate results.
Examples & Analogies
Imagine you're trying to build a model of a river. Just as you'd follow guidelines to ensure your model flows correctly, following hints while applying equations ensures that our calculations reflect the actual fluid conditions.
Fixed Control Volume Simplification
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
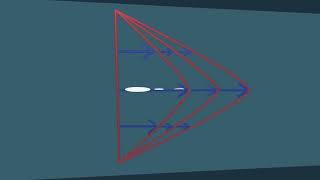
Now go for a simple problems, where you have a linear momentum equations like you have a fixed control volume, just to look at, you have a fixed control volume. There are the in are there, okay, and there are the outs are three, and this is a fixed control volume. So there is inflows, this is outflows.
Detailed Explanation
Here, the lecturer explains how to analyze a fixed control volume with multiple inflows and outflows while applying linear momentum equations. This involves summing the forces acting on the control volume to understand the fluid movements betting distributed.
Examples & Analogies
Consider a water tank with several pipes: some pipes supply water while others drain it. By keeping track of how much water enters and exits, we can balance everything out and understand the tank's changing water levels.
Net Force Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The sum of the force component to what this control volume that what will be the net out flux of momentum fluxes through these control surface.
Detailed Explanation
This portion discusses calculating the net force acting on a control volume based on the momentum fluxes coming in and going out. The importance of capturing these inflows and outflows accurately is emphasized for obtaining correct results.
Examples & Analogies
If you think of a car going through a tunnel, all the air entering and exiting the tunnel leads to a push against the car. Understanding the amounts of air flowing in and out helps us figure out how much force the car experiences as it moves through.
Steady Flow with One Inlet and One Outlet
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let us go for another simplifications. That in a steady flow conditions, okay and only one outlet one inlet, this is very simplified case. See when you have one inlet and one outlet...
Detailed Explanation
In steady flow with only one inlet and one outlet, mass inflow equals mass outflow, and thus can be simplified to a basic conservation equation. Understanding this simplification allows for easier calculations without losing accuracy.
Examples & Analogies
Imagine a simple garden hose where one end is underwater, and the other end delivers water to the garden. If the same amount of water comes in as it goes out, it's easy to predict how much water will flow to the garden.
Considering External Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now if you look it another set of the problems we solve it, where there is no external forces is there...
Detailed Explanation
Here, the lecturer covers scenarios where there are no external forces acting on the fluid dynamics. The resulting equation simplifies further, emphasizing the relationship between momentum flux and control volume changes.
Examples & Analogies
Think about a soccer ball in mid-air: without wind or player interference, we can easily predict where the ball will land based on its momentum alone. Similarly, in fluid dynamics, observing the fluid's natural flow helps clarify the outcomes.
Tips for Applying Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now comes back to the, what are the tips are there, when you apply the linear momentum equation...
Detailed Explanation
In this concluding chunk, the lecturer provides key reminders when working with linear momentum equations, stressing the importance of considering vector components and momentum flux terms. These reminders ensure comprehensive analysis for successful calculations.
Examples & Analogies
It's like cooking: following the recipe completely, including every step and ingredient, ensures that nothing essential is missed, leading to a delicious meal. Similarly, diligently applying all necessary steps in physics results in accurate predictions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Control Volume: The region analyzed to study fluid and momentum flow.
-
Momentum Flux: The product of mass flow rate and velocity in a given direction.
-
Steady Flow: A condition in which fluid properties at a point do not change with time, simplifying analyses.
-
Body Forces: Forces acting throughout the volume of an object, such as gravity.
-
Surface Forces: Forces acting on the surface of the control volume due to pressure.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of a fixed control volume analysis using a water jet to compute force components.
-
Example calculations involving momentum flux correction factors in a non-uniform pipe flow.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Flow steady as you go, control volume to and fro.
📖 Fascinating Stories
-
Imagine a river flowing steadily through a bridge, where we analyze how the water interacts with pier sections. This is our control volume approach!
🧠 Other Memory Gems
-
Remember the acronym 'SMILE' for analyzing flows: Steady state, Momentum, Inlets and outlets, Look for forces, Evaluate results.
🎯 Super Acronyms
Use 'FAST' for simplifications
- Fixed control volume
- Analytical approach
- Steady assumption
- Total momentum.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Control Volume
Definition:
A defined region in space through which fluid flows for analysis.
-
Term: Momentum Flux Correction Factor
Definition:
A factor that accounts for variations in velocity across a non-uniform section.
-
Term: Reynolds Transport Theorem
Definition:
A fundamental statement in fluid mechanics that connects the changes in a system to the flow across its boundaries.
-
Term: Body Forces
Definition:
Forces that act on a body due to gravity or other fields, not due to contact.
-
Term: Surface Forces
Definition:
Forces that arise from pressure and shear acting on the surface area of a control volume.