Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Overview of Linear Momentum Conservation
Unlock Audio Lesson
Today we are discussing the principles of linear momentum equations in fluid mechanics. Can anyone tell me why conservation of momentum is important?
It's crucial for understanding how fluids behave in various engineering applications!
Exactly! We use Reynolds transport theorem to express these principles mathematically. It's essential for managing fluid dynamics efficiently in engineering.
What is a control volume?
A control volume is a defined space where we analyze the momentum, mass, or energy changes occurring within. They can be fixed or moving, depending on our analysis. We analyze the forces acting, which include body and surface forces.
So, surface forces include pressure and reaction forces, correct?
That's right! Don’t forget that body forces, like gravity, also play an essential role in momentum equations. Remember the acronym F = ma for force, mass, and acceleration.
I like that! It helps me remember how to connect force and momentum.
Great! We will delve into examples and see how these concepts apply practically. Let's summarize what we've talked about.
Applying Momentum Equations
Unlock Audio Lesson
Now, let's explore how to apply momentum equations. Who remembers the importance of conservation of mass in fluid dynamics?
It's about ensuring mass does not accumulate or vanish in a flow.
Exactly! In our linear momentum equations, for steady flow, the mass coming in equals the mass going out. This gives us a solid foundation to apply force equations.
Can we look at a problem involving one inlet and one outlet?
Sure! If we have one inlet and one outlet in a control volume, the momentum flow can be defined using the relationship between mass flux and velocity. Let's consider the formulas.
So we use mass flow rates and the momentum correction factors for varying velocity!
Exactly! Momentum flux correction factors are needed in real applications where fluid flow is non-uniform.
That's helpful! We could simplify to find forces when no external forces are acting, right?
Yes! If there are no external forces, the sum of the forces equals zero, simplifying our calculations. Remember to visualize the entire situation with diagrams.
Momentum Flux Correction Factors
Unlock Audio Lesson
Now let's dive deeper into momentum flux correction factors. Does anyone know why these are important?
They help account for the difference in velocity distribution across a cross-section.
Correct! If the velocity distribution is uniform, the correction factor is 1, but in reality, it's often not. Let’s calculate the factors in a typical problem.
Do these factors apply to all types of flow?
Good question! They are particularly crucial in turbulent and unsteady flows where velocity distributions can vary significantly. Let’s remember the formula: it involves the average and actual velocities.
How can we visualize their impact?
Think about a river. The center typically flows faster than the edges, which affects how momentum is conveyed. You’ll often observe variations in flow speed—this is where corrections matter!
That really clarifies things. I’ll keep that in mind for future problems.
Practical Applications of Momentum Principles
Unlock Audio Lesson
Finally, let’s connect everything we’ve learned with real-world applications. Can anyone share an example?
Um, the flow of water through a dam?
Yes! In a dam scenario, we analyze how the force of water impacts structures. The outlet velocity, its pressure, and the forces acting are crucial. Always remember: F=ma applies here too!
I’d like to explore how this might apply to design safety!
Absolutely! Safety designs must account for maximum possible flows and forces that might occur. Simulating scenarios helps engineers prepare for unexpected outcomes.
This sounds like crucial knowledge for future projects!
Indeed! Always relate the math with real-world implications—it makes the learning meaningful. Let’s recap the main points.
We covered linear momentum equations, control volumes, conservation laws, and importance of momentum flux correction factors. Remember to visualize each situation for better understanding!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the concepts of conservation of momentum using Reynolds transport theorem and control volumes are examined. Simplifications of momentum equations under various conditions, such as fixed and moving control volumes, are discussed, alongside examples and applications of these principles in engineering contexts.
Detailed
Detailed Summary
This section discusses the principles of linear momentum equations, emphasizing their significance in fluid mechanics. The focus is on the conservation of momentum, which is a critical concept for analyzing the behavior of fluids under various conditions. Key concepts include the Reynolds transport theorem, the application of control volumes (both fixed and moving), and the distinction between body and surface forces acting on these volumes.
Additionally, the section elaborates on the momentum flux correction factors, which are necessary for dealing with non-uniform velocity distributions across cross-sections. Several engineering applications, such as calculating forces on control volumes, are illustrated through examples, including steady flow conditions, one inlet and one outlet scenarios, and the influence of external forces. The narrative also advises students on necessary hints and tips for applying these equations correctly, ensuring a foundational understanding of fluid mechanics principles.
Youtube Videos
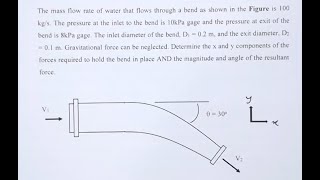
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Linear Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come to today's lecture, will have a steady flow across missions for the linear momentum equations. Many of the times, we have a linear momentum equations we solve for the one inlet or one outlet and in one directions and some of the problems we have solved with no external forces, then how the momentum equations can be simplified.
Detailed Explanation
In fluid mechanics, linear momentum equations help us understand how momentum changes in a flow system. When analyzing fluid flow, often we focus on systems with various inlets and outlets. It's important to identify if there are any external forces acting on the system which can simplify the equations. If there are no external forces, the equations can be reduced, making them easier to solve while still capturing the essence of the physical situation.
Examples & Analogies
Imagine a water slide. When you slide down without any external pushes (like wind or other people), the way you gain speed can be compared to how momentum equations predict fluid behavior without external forces. Just like you speed up due to gravity alone, fluids follow predictable patterns without outside pushes.
Control Volume Concept in Momentum Flux
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, go for a simple problems, where you have a linear momentum equations like you have a fixed control volume, just to look at, you have a fixed control volume. There are the in are there, okay, and there are the outs are three, and this is a fixed control volume. So there is inflows, this is outflows. There is inflows and outflows.
Detailed Explanation
Control volume is a defined region in space through which fluid can flow in and out. In this context, we consider inflows and outflows to utilize linear momentum equations effectively. For a steady-state flow in a fixed control volume, we assess how the forces acting within the control volume depend on the momentum flux—how much momentum comes in versus how much goes out. This balance leads to understanding the net forces acting on the system.
Examples & Analogies
Think of a roundabout. The cars (flowing fluid) entering and exiting create a balance within the roundabout. If too many cars enter without enough exiting, it may cause congestion (a buildup of momentum). By analyzing the number of cars entering and exiting, we can control traffic flow, much like controlling momentum in fluid systems.
Application of Momentum Flux Correction Factors
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, considering this, in these control volume, fixed control volume, what will be the net force which will be acting on these will be considered as a steady problem, then you will have these conditions, okay. You can easily find out if it is a steady problem, you will have a definitely the net mass influx, in should equal to the net mass influx going out from this.
Detailed Explanation
When analyzing fixed control volumes, it is essential to ensure mass coming in equals mass going out (mass conservation). This relationship simplifies how we apply the momentum equations. The net force acting on the system can be derived from these mass flow rates. More critically, we consider momentum flux correction factors to account for non-uniform velocity distributions, helping to refine our calculations in practical situations.
Examples & Analogies
Imagine a water tank with an inflow pipe and multiple outflow pipes. If water inflows (mass influx) exactly match the outflows, the tank remains stable (steady state). However, if the water level fluctuates, it can signify uneven outflows or varying flows—much like the correction factors help us understand the real flow dynamics in a fluid system.
Special Cases for Simplification
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, let us go for another simplifications. That in a steady flow conditions, okay and only one outlet one inlet, this is very simplified case. See when you have one inlet and one outlet, if your mass influx is inflow is coming into that, your mass influx out will be. That means Q1 = Q2, that is a very basic equations what we get it, if we apply the conservations of mass.
Detailed Explanation
In simpler models with one inlet and one outlet, the relationships between inflow and outflow become straightforward. This scenario allows us to apply the principle of conservation of mass directly, leading us to a basic equation where the mass inflow equals the mass outflow. Such simplifications enable quicker problem-solving and deeper comprehension of the system dynamics.
Examples & Analogies
Picture a simple water pitcher pouring into a glass. The amount of water entering the glass (inflow) equals the amount leaving the pitcher (outflow). This consistent balance reflects conservation of mass, akin to how fluid systems with one inlet and outlet function in a predictable manner.
Using Vector Components in Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, there are the problems where is come it, very interestingly that we can apply the momentum equations as you can go it, this momentum equation is a vector equation, it has a three components in scalar directions, X component, Y component, Z component.
Detailed Explanation
Momentum equations are vector equations composed of three components corresponding to the x, y, and z directions. When solving a problem, focusing on one direction can simplify the analysis while still providing the necessary insights into the overall behavior of the flow. Understanding the interplay between these vector components is critical for accurate modeling.
Examples & Analogies
Consider playing baseball. When throwing a ball, its motion can be divided into horizontal (x) and vertical (y) components. If a batter focuses only on one direction—like throwing straight rather than at an angle—they can simplify their technique while still achieving a good result on the field. Understanding all components can enhance overall performance.
Momentum Equation Simplification in Absence of External Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now comes back to the, what are the tips are there, when you apply the linear momentum equation. First thing is that do remember is momentum equations is a vector equation, it has a three scalar components, it has the directions.
Detailed Explanation
In circumstances where no external forces act on a system, the momentum equation simplifies significantly. Under these conditions, we can equate the rate of change of momentum within the control volume directly with the differences in incoming and outgoing momentum flux. This streamlining assists in focusing on essential flow behaviors without external complexities.
Examples & Analogies
Imagine a sled on a flat surface with no wind or obstacles. The sled's steady motion represents how momentum factors work in isolation—without outside influences affecting its speed or direction. Understanding this concept helps manage other real-world systems effectively.
Tips for Applying the Linear Momentum Equations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
And the last one is what is that the fluid when it exists subsonically, that means flow is subsonic flow, Mach number is less than 1. In that case, if flow exits to atmospheric conditions, you can always consider the fluid pressure is atmospheric pressures.
Detailed Explanation
Applying linear momentum equations effectively requires a clear understanding of the flow conditions and assumptions made during the calculations. Special cases, like when the flow is subsonic, enable simplifications, especially concerning pressure conditions. Recognizing when these assumptions are valid helps streamline calculations and refine predictions of fluid behavior.
Examples & Analogies
Think of a low-speed train moving through a station. As it slows, the air pressure around it stabilizes, much like subsonic flows reaching atmospheric pressure. Understanding this equivalence can help optimize designs that operate under similar conditions in the real world.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Conservation of momentum is crucial in analyzing fluid behavior.
-
Control volumes help visualize and manage fluid dynamics.
-
Momentum flux correction factors account for velocity variations in non-uniform flow.
-
Understanding body and surface forces is essential for momentum calculations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating forces acting on a bridge pier under flowing water.
-
Analyzing the momentum change in fluid exiting a nozzle.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Momentum flows fast, don't let it pass, keep your control volume tight, and hold on to that might.
📖 Fascinating Stories
-
A water jet hits a wall; the reaction force pushes back, illustrating the conservation of momentum in action.
🧠 Other Memory Gems
-
To remember the types of forces: Body forces act without a contact, but surface forces are right there, don't forget that!
🎯 Super Acronyms
C.M.B.S. - Control Volume, Mass conservation, Body and Surface forces.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Linear Momentum
Definition:
A measure of the motion of an object calculated as the product of its mass and velocity.
-
Term: Control Volume
Definition:
A specified volume in space through which fluid flows, aiding in the analysis of momentum and mass.
-
Term: Reynolds Transport Theorem
Definition:
A mathematical formulation that relates the time rate of change of a quantity (like momentum) within a control volume to the flux of that quantity across the control surface.
-
Term: Momentum Flux Correction Factor
Definition:
A factor used to correct the calculation of momentum flux when velocity distributions are non-uniform across a cross-section.
-
Term: Body Forces
Definition:
Forces that act throughout an object, like gravity, rather than on its surface.
-
Term: Surface Forces
Definition:
Forces that act upon the surface of an object, including pressure forces and shear forces.