Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fixed Control Volumes
Unlock Audio Lesson
Today, we'll explore the concept of fixed control volumes. A fixed control volume is a defined space in which we analyze fluid flow. Can anyone tell me why control volumes are important in fluid mechanics?
Is it because they help simplify the analysis of fluid motion?
Exactly! They allow us to apply conservation laws easily. Remember, we can analyze how mass, momentum, and energy behave in this fixed region. Let's consider a mnemonic to help us remember these laws: 'MEF' stands for Mass, Energy, Force. So, what do we understand about the forces acting on these volumes?
Are they body forces and surface forces?
Correct! Body forces include gravitational forces, while surface forces are related to pressure and reaction forces. Let's summarize: Fixed control volumes simplify fluid analysis by applying conservation laws—mass, energy, and force.
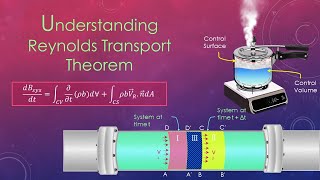
Reynolds Transport Theorem and Simplifications
Unlock Audio Lesson
Now that we understand fixed control volumes, let's talk about Reynolds Transport Theorem. Who can summarize what it does?
It connects the system approach with the control volume approach to analyze various fluid properties.
Precisely! This theorem helps frame conservation equations neatly. When we deal with simplifying assumptions—like steady-state flow—how do we reduce the equations?
If we assume no change over time, we can set time derivatives to zero.
Correct! When time derivatives vanish during steady-state, we simplify the momentum equations. Always remember: simplifications lead to less complex calculations.
Engineering Applications of Fixed Control Volume Concept
Unlock Audio Lesson
Let's transition to practical applications. When analyzing flow through a fixed control volume, what should we assess regarding forces?
We need to look at both inflow and outflow momentum and consider the net force acting on the control volume.
Exactly! The net force is the difference between inflow and outflow momentum fluxes. And what about momentum flux correction factors—why are they necessary?
They adjust for non-uniform velocity distributions.
Right! For real-world engineering problems, acknowledging these factors is crucial. Now, can anyone recall key assumptions we make during these analyses?
Steady flow conditions and one inlet or outlet!
Excellent! Remember these assumptions for efficient problem-solving.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section covers the principles of fixed control volumes, the use of Reynolds transport theorem in fluid mechanics, and how these concepts apply to engineering problems involving flow and forces. It emphasizes the simplifications involved and the considerations in momentum equations.
Detailed
Detailed Summary
The concept of a fixed control volume plays a crucial role in fluid mechanics, particularly in the application of the conservation of momentum. This section introduces the fixed control volume framework, contrasted with moving control volumes, and explains its relevance to analyzing fluid behavior through the Reynolds transport theorem.
Key Points Covered:
- Control Volume Concept: Control volumes are defined regions in space across which fluid flows, allowing for the analysis of mass, momentum, and energy conservation.
- Reynolds Transport Theorem: This theorem connects the system (a fixed amount of fluid) and control volume approaches, providing a framework to analyze fluid mechanics phenomena.
- Forces Acting on Control Volumes: The section elaborates on body forces (like gravity) and surface forces (such as pressure) acting on a control volume, and how to evaluate them.
- Momentum Flux Correction Factors: When dealing with non-uniform velocity distributions, momentum flux correction factors should be incorporated into calculations to ensure accuracy in momentum flow.
- Simplifications in Momentum Equations: Utilizing assumptions such as steady flow and one inlet/outlet conditions simplifies the momentum equations significantly.
- Engineering Applications: Several examples illustrate how to compute forces and evaluate momentum using the principles discussed, emphasizing practical applications in civil and mechanical engineering.
This foundational understanding is essential for mechanical and civil engineering applications, as it lays the groundwork for more complex fluid dynamics problems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Fixed Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now, go for a simple problems, where you have a linear momentum equations like you have a fixed control volume, just to look at, you have a fixed control volume. There are the in are there, okay, and there are the outs are three, and this is a fixed control volume. So there is inflows, this is outflows. There is inflows and outflows.
Detailed Explanation
In fluid mechanics, a fixed control volume is a defined region in space through which fluid can flow. The key concept is that we analyze the flow into and out of this volume. In this scenario, we have multiple inlets (inflows) and outlets (outflows). This means fluid enters the control volume from some points and exits from others. The balance of mass and momentum is what we will analyze within this fixed volume.
Examples & Analogies
Imagine a large tank with water flowing in through a faucet (inflow) while simultaneously draining out through several holes at the bottom (outflows). This tank represents our fixed control volume. As water comes in from the faucet while also flowing out from holes, we can study how the water levels change inside the tank, which relates closely to the concepts of mass and momentum conservation.
Momentum Equations for Steady Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The sum of the force will be act on these, if it is a steady linear momentum equations. The time derivative components become 0, so we will have a sum of force is equal to, this is still I am putting in a vector notation is equal to the, in case of steady, the difference between the rate of outgoing and incoming momentum fluxes.
Detailed Explanation
When analyzing momentum in a steady flow situation, any changes in momentum over time (time derivatives) are zero because the fluid properties are constant. Thus, the overall momentum of the control volume can be defined by the forces acting on it. The net force acting on the control volume equals the difference between the momentum flux entering the control volume and the momentum flux exiting it. This is crucial for balancing the forces.
Examples & Analogies
Think of a revolving door at a shopping mall. When people (momentum) push through the door from one side (inflow), they either leave the door from the other side (outflow) or come to a halt inside. The net movement of people (momentum) in and out of the door mimics how we balance incoming and outgoing momentum in our fixed control volume. If more people are exiting than entering, someone could analyze the pressure on the door hinge (force).
Applying Momentum Flux Corrections
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, what we will do it, some of the momentum flux, what is coming as an inflow, that the mass flux into the velocity that is a momentum flux, then we have the beta one and beta two, which is representing momentum flux correction factors, which will differ from the one to 1 to 2 3 4 5 locations because the velocity distributions are the different.
Detailed Explanation
Momentum flux is derived from the product of mass flux and velocity. In non-uniform flow, the velocity isn't the same everywhere across a given section. Therefore, we use momentum flux correction factors (beta values). These factors adjust our calculations based on actual fluid dynamics to provide more accurate estimates of momentum flux. Depending on where you measure the velocity, these factors can differ since they account for variations in flow speed and distribution.
Examples & Analogies
Think of a river whose speed varies depending on location. Near the banks, the water flows slower due to friction with the land, while in the center, it's faster. If you're measuring the total flow at a bridge, you need to consider how the speed varies from those slow banks to the fast middle portion. Similar to using beta values, you’d average the flow across the entire width to get an accurate picture of the river's overall momentum.
Net Forces Acting on Control Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The sum of the force component to what this control volume that what will be the net out flux of momentum fluxes through these control surface. So, in this case, we have three outlets, two inlets.
Detailed Explanation
The net forces acting on our fixed control volume can be obtained by calculating the total momentum flux entering and exiting the volume. This involves analyzing the three outlets and two inlets previously mentioned. For steady flow, we can equate the sum of the inflows and outflows, allowing us to derive the resultant force acting on the control volume, which dictates changes in motion or velocity.
Examples & Analogies
Picture a large aquarium with four outlets providing water back to a filtration system while two inlets supply fresh water. Monitoring the total inflow versus the total outflow allows us to understand how clean or effective our tank is at maintaining its environment. The balance helps us know if we need to adjust the input of fresh water or the capacity of the filtration system.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Fixed Control Volume: A defined region for analyzing fluid flow and properties.
-
Reynolds Transport Theorem: Connects system and control volume approaches for fluid analysis.
-
Forces in Control Volumes: Examination of body and surface forces acting on fluids.
-
Momentum Flux Correction Factors: Adjust for non-uniform velocity distributions to ensure accuracy.
-
Steady Flow Assumptions: Simplifications made during analysis for easier calculations.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating forces acting on a bridge pier when fluid flows around it.
-
Using momentum flux corrections in a flow analysis for a non-uniform velocity field.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In the flow of life, momentum we steer, with fixed volumes to hold, what we hold dear.
📖 Fascinating Stories
-
Imagine a river flowing through a canyon – the water is like the movement of ideas, captured in a defined space (the canyon) where we can analyze it closely.
🧠 Other Memory Gems
-
MEF: Mass, Energy, Force helps remember the analysis aspects of control volumes.
🎯 Super Acronyms
FUV
- Fixed
- Uniform
- Volumes for easy remembrance of the fixed control volume concept.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Fixed Control Volume
Definition:
A defined volume in which fluid properties are analyzed, assuming no movement of the volume itself.
-
Term: Reynolds Transport Theorem
Definition:
A theorem that relates the change of a quantity within a control volume to the flow of that quantity across the control volume's boundaries.
-
Term: Body Forces
Definition:
Forces acting on a fluid body due to external fields, such as gravity.
-
Term: Surface Forces
Definition:
Forces acting on a fluid at its surface, mainly due to pressure and reaction forces.
-
Term: Momentum Flux Correction Factors
Definition:
Factors used to account for non-uniform velocity distributions in momentum calculations.
-
Term: Steady Flow
Definition:
A flow condition where fluid properties at a point do not change over time.