Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Flow Types
Unlock Audio Lesson
Welcome everyone! Today we are discussing the types of fluid flow: compressible and incompressible. Can anyone tell me what they understand by these terms?
I think incompressible flow means the density doesn’t change, right?
And compressible flow is when the density can vary, like in gases.
Exactly! Incompressible flow typically assumes constant density, simplifying our calculations. Remember the acronym 'KISS': Keep It Simple, Students—this is why we often use incompressible assumptions in engineering.
What are some scenarios where we can't assume incompressibility?
Good question! High-speed gas flows are a common example where density changes become significant, leading us to use compressible flow analysis.
So, for water flow in pipes, we use incompressible flow most of the time?
Correct! In fluid mechanics, many applications rely on incompressible assumptions for liquids due to very small density changes.
Applying Reynolds Transport Theorem
Unlock Audio Lesson
Now let’s discuss the Reynolds transport theorem. How do we apply it differently for compressible versus incompressible flows?
Isn’t it that for incompressible flow, we set density to a constant?
Exactly! When density is constant, it simplifies our surface integral calculations. But in compressible flows, we consider density as a variable.
Does that mean we have to handle more variables and calculations for compressible flow?
Yes! More complexity means we must be careful with our momentum equations, especially when dealing with time-dependency.
Could you give an example of what types of problems we would solve for each flow type?
For incompressible flow, we often look at water flow in pipes or open channels. While for compressible flow, we might analyze the flow of air around an airplane wing.
Practical Examples and Applications
Unlock Audio Lesson
Let’s discuss some practical applications. Can anyone think of a real-world scenario involving compressible flow?
How about when a plane is flying at high altitudes? The air around it compresses.
Exactly! At high speeds, the changes in air density are noticeable and crucial for performance analysis. Similarly, what about an example of incompressible flow?
Water flowing in a residential pipe system!
Correct! The density remains essentially constant, so we can apply simpler calculations based on incompressible flow assumptions.
Would temperature changes affect the compressibility of the air?
Absolutely! High temperatures can lead to greater variations in density, making compressible flow analysis necessary. Remember, temperature, and pressure primarily govern compressibility.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on the differences between compressible and incompressible flow, specifically how density variation affects the analysis and application of momentum equations. Understanding these flow types is crucial for simplifying calculations in fluid mechanics applications.
Detailed
In fluid mechanics, understanding flow classifications is vital for correctly applying principles and equations. This section focuses on the distinctions between compressible and incompressible flows. It explains that incompressible flow assumes constant density, simplifying momentum conservation equations significantly. This is commonly applied in practical situations like engineering devices. Conversely, compressible flow involves variations in density, necessitating more complex mathematical treatments. The discussion introduces Reynolds transport theorem as a foundational principle for both flow types, highlighting how time-dependence and density variations dictate which assumptions can be made during analysis.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Definitions of Flow Types
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
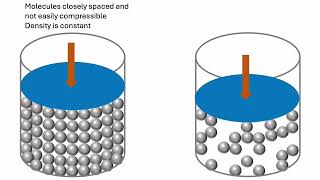
The flow is classified into compressible and incompressible based on density variations. If density varies significantly, the flow is considered compressible. If density remains essentially constant, the flow is incompressible.
Detailed Explanation
In fluid mechanics, the distinction between compressible and incompressible flow is crucial. Compressible flow occurs when the density of the fluid changes significantly due to pressure variations, typically in gases. For example, when air moves fast enough to change pressure greatly, such as in jet engines, the flow is compressible. On the other hand, incompressible flow assumes the density remains constant throughout the fluid, which is a common assumption in many engineering applications involving liquids, such as water in pipes.
Examples & Analogies
Think of a balloon. When you inflate it, the air density inside the balloon changes as its volume increases; this is similar to compressible flow. Conversely, when you pour water from one glass to another, the density of the water remains unchanged, illustrating incompressible flow.
Impact on Calculation Simplifications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In the case of incompressible flow, it leads to significant simplifications in calculations. The density can be treated as a constant, which simplifies the application of the Reynolds transport theorem.
Detailed Explanation
When you assume a flow is incompressible, calculations become much easier. The mass equation simplifies because you don't have to continuously account for changing density. Instead, density can be removed from the equations, and you only need to focus on the velocity and area during surface integrals. For example, with incompressible flow, the mass flow rate can be calculated straightforwardly as the product of area and velocity without adjusting for density changes.
Examples & Analogies
Imagine trying to measure how much water flows from a faucet into a bucket. If the water's density could change while flowing (which is mainly only true for gases under certain conditions), you would need complex calculations. But since water's density doesn't change much, you can simply use the flow rate formula, making it much easier.
Applications in Engineering
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Most engineering problems assume steady incompressible flow, which simplifies their analysis and design.
Detailed Explanation
In engineering, especially when dealing with liquids, the assumption of steady incompressible flow allows for simpler design calculations in systems like pipelines, water treatment plants, and irrigation systems. When engineers model fluid systems, they often use the incompressible assumption so they can easily apply conservation equations without the need for complex density adjustments.
Examples & Analogies
Consider a large pipeline transporting water to a city. Engineers can model the flow as incompressible to quickly design the necessary pipe sizes and pump requirements, ensuring efficient delivery without getting bogged down by complex calculations that would arise if the water were treated as compressible.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Density Variation: The difference between compressible and incompressible flows lies in how density is treated during analysis.
-
Momentum Equations: Incompressible flow allows for simplifications in momentum equations, while compressible flow demands more extensive analysis.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Airflow over an airplane wing, where compressibility affects lift and drag.
-
Water flow in a pipe system, where assumptions of constant density simplify calculations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
When density shifts, and pressure lifts, that’s compressible flow, where the density’s on the go.
📖 Fascinating Stories
-
Imagine a balloon being squeezed; the air inside compresses. This showcases compressible flow; in contrast, a steady pipe of water flows unchanged, representing incompressible flow.
🧠 Other Memory Gems
-
Remember 'DIP' for Different behavior in flow: Density Invariant for Incompressible and Density Varies for Compressible.
🎯 Super Acronyms
CC
- Compressible Change
- IC
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Compressible Flow
Definition:
Flow in which density varies significantly with pressure and temperature changes.
-
Term: Incompressible Flow
Definition:
Flow in which density remains nearly constant regardless of pressure changes.
-
Term: Reynolds Transport Theorem
Definition:
A mathematical statement that relates fluid motion and changes in control volume properties over time.