Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Reynolds Transport Theorem
Unlock Audio Lesson
Today, let's start with the Reynolds transport theorem, a fundamental concept in fluid mechanics that helps relate the flow of fluid in a control volume to physical properties like mass and momentum.
What exactly does the Reynolds transport theorem allow us to do in fluid mechanics?
Great question! It enables us to convert system equations related to fluid properties into a form that can be applied to a control volume. This means we can analyze changes over time, relating them to net fluxes across the control surface.
Can you explain the difference between extensive and intensive properties again?
Of course! Extensive properties depend on the amount of substance—like mass or volume—while intensive properties are independent of the amount of substance—like pressure and temperature.
What about steady versus unsteady flow? How does that come into play?
Good observation! In steady flow, properties at any given point do not change over time. In unsteady flow, on the other hand, properties can vary, requiring careful analysis over time. Remember: in steady flow, the time derivatives become zero!
So, if we have constant density, the calculations should be simpler?
Exactly! A constant density allows us to simplify our calculations significantly by making mass terms scalar products, hence easing the integration processes.
In summary, the Reynolds transport theorem is essential as it provides the necessary framework for applying the conservation of linear momentum in engineering problems. Remember, flow details and properties dictate the complexity of the conservation equations.
Application of Linear Momentum Equations
Unlock Audio Lesson
Now let’s move on to how we can apply linear momentum equations to specific fluid scenarios. Where do you think these equations are most applicable?
Maybe in systems with lots of moving parts like turbines?
Exactly, turbines are a prime example! They rely on the principles of fluid momentum conservation to optimize efficiency and output.
How do we account for different forces acting on our control volume?
Great inquiry! We consider body forces, like gravity, acting throughout the control volume, and surface forces, such as pressure and viscous forces, which act across the control surfaces.
How do we derive those equations?
We start with the overall momentum balance, factoring in all forces—body and surface—that affect the fluid motion within our control volume. Then we derive the linear momentum equations based on these interactions.
And what about our assumptions in these analyses?
Assumptions are vital! For example, assuming incompressible flow helps streamline calculations. Notably, working within fixed or moving control volumes also alters our approaches.
To recap, applying linear momentum equations allows us to solve practical engineering problems effectively by considering the forces at play within fluid systems.
Understanding Flow Types and Their Implications
Unlock Audio Lesson
Let's discuss the types of flow and their implications for conservation equations. Which types can you identify?
Incompressible and compressible flows?
Correct! Incompressible flow assumes constant density, simplifying our analysis. Compressible flow, however, introduces complexities due to varying densities.
What about laminar versus turbulent flows?
Excellent! Laminar flow is smooth and orderly, while turbulent flow is chaotic and highly mixed. Each affects momentum conservation differently; turbulent flows generally require advanced modeling techniques.
How can we visualize these concepts?
Visual aids, like flow diagrams and pictorial representations of streamlines, can greatly enhance your understanding of these flow behaviors.
So, knowing the flow characteristics helps with choosing the right equations?
Absolutely! The type and nature of flow guide us in deciding which conservation equations to apply and how to simplify them effectively.
In summary, understanding flow types is crucial for applying conservation principles accurately in fluid mechanics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section presents the derivation of the conservation of linear momentum, emphasizing the Reynolds transport theorem, fixed and moving control volumes, and the implications of steady and unsteady flows. Notable examples and applications illustrate the practical utilization of these concepts in fluid mechanics.
Detailed
Detailed Summary on the Derivation of Conservation of Linear Momentum
This section focuses on the derivation of the conservation of linear momentum within the context of fluid mechanics. The conservation of momentum is a fundamental principle that describes how the momentum of a fluid system is conserved under various conditions. The approach is founded on the Reynolds transport theorem, which provides a framework for linking the system behavior to its control volume.
Key concepts discussed include:
- Reynolds Transport Theorem: This theorem acts as a cornerstone for analyzing fluid flow, allowing simplification of the equations governing flow by considering extensive and intensive properties and establishing conditions for steady or unsteady flows.
- Control Volumes: The analysis is performed on both fixed and moving control volumes, illustrating how momentum can be calculated based on forces acting on the fluid contained within these volumes.
- Flow Classifications: Different flow types, such as incompressible and steady flows, are addressed, showcasing how these influence the calculations of momentum conservation equations.
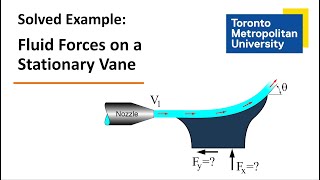
- Examples and Applications: Practical examples, such as hydroelectric projects, are referenced to contextualize the applications of the momentum conservation principles in real-world scenarios. The derivation culminates in the establishment of linear momentum equations that can be employed in various engineering applications.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Control Volume Concept
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
We will consider the control volumes, we have considered the control volume like this. So, each control volume has the control surface. It could be a very simple tetrahedral type of structure or you can have very complex, it does not matter what could be the shapes.
Detailed Explanation
In fluid mechanics, a control volume is a defined region in space through which fluid can flow. It's important to understand that control volumes can have various shapes, ranging from simple geometric forms to complex structures. Each control volume has a defined boundary known as the control surface, which allows us to analyze how mass, momentum, and energy change as fluid flows in and out.
Examples & Analogies
Think of a control volume like a swimming pool. You can imagine the pool as a defined volume of space, where the water level rises and falls based on how much water is added or drained. The surface of the water represents the control surface, and analyzing how water flows in and out helps you understand things like filling the pool or draining it.
Forces Acting on Control Volume
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at that, over that surface what will happen is you will have normal vectors, let dA be the surface area, over that is the normal vector to the surface area. So, you will have the surface which will have two types forces going to act on this.
Detailed Explanation
Within a control volume, there are two primary types of forces: body forces and surface forces. Body forces, like gravity, act throughout the entire volume of the fluid, while surface forces act on the boundaries of the control volume, such as pressure and viscous forces. Recognizing the differences between these forces is crucial for analyzing fluid behavior and deriving equations governing movement.
Examples & Analogies
Imagine holding a balloon filled with water. The weight of the water inside the balloon represents the body force acting downward due to gravity. At the same time, if you squeeze the balloon on the outside, you're applying a surface force on the boundary, affecting how the water moves inside. Understanding both types of forces helps us analyze how the water behaves in response.
Calculating Gravity Force
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If I take a small element dV, I will have the weight of these small control volumes, it will be ρg dV.
Detailed Explanation
To calculate the gravitational force within a control volume, we consider a small elemental volume (dV) and multiply its density (ρ) by gravity (g) and the volume (dV). This gives us the weight of that small element. Since gravity acts on every part of the control volume, summing these individual weights helps us determine the total gravitational force acting on the entire control volume.
Examples & Analogies
Consider a stack of books on a table. Each book has a weight, and the total weight pressing down on the table is the sum of all the individual weights of each book. Similarly, when analyzing a control volume in fluid mechanics, we sum up the gravitational forces from each tiny element of fluid to find the overall force acting downwards.
Surface Forces and Their Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you want the result as the x and y component, that is your Cartesian coordinates, that is what is different here. One is the Cartesian coordinate level resolving the force vector component to a scalar component in x and y direction.
Detailed Explanation
Surface forces acting on the boundaries of a control volume can be resolved into components. These components can be normal (perpendicular to the surface) or tangential (parallel to the surface). By breaking forces down into their x and y components, which are defined in Cartesian coordinates, it simplifies the analysis and helps in applying mathematical methods to solve fluid flow equations.
Examples & Analogies
Picture holding a flat rectangular piece of cardboard. If you push down on one side at an angle, the force can be broken down into two parts: one that pushes straight down (normal) and another that pushes sideways (tangential). This breakdown makes it easier to calculate how the cardboard will respond to your push, just as it's easier to analyze forces in fluid mechanics when they're decomposed into components.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Reynolds Transport Theorem: A mathematical framework for relating system dynamics to control volumes.
-
Conservation of Momentum: The principle stating that momentum within a closed system is conserved, barring external influences.
-
Control Volumes: Defined regions utilized in analyzing fluid dynamics, having well-defined boundaries.
-
Flow Classification: Categorization of flow types (steady vs unsteady, compressible vs incompressible, turbulent vs laminar) that affect momentum conservation.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
The behavior of water in a pipe during steady, incompressible flow can be analyzed using the conservation of momentum equations.
-
In hydroelectric dam design, momentum conservation principles are used to predict water flow and energy generation.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Momentum flows with ease, keep it constant, if you please.
📖 Fascinating Stories
-
Imagine a river (the control volume) flowing smoothly with no outside interference, maintaining its momentum as it rushes along.
🧠 Other Memory Gems
-
In sesions of fluid dynamics, remember 'R-C' – Reynolds and Conservation.
🎯 Super Acronyms
M-L-T (Momentum, Linear, Transport) helps remember the key concepts.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Conservation of Momentum
Definition:
A principle stating that the total momentum of a closed system remains constant if no external forces act on it.
-
Term: Reynolds Transport Theorem
Definition:
A theorem that provides a relationship between the rate of change of a quantity within a control volume and the flow of that quantity across the control surface.
-
Term: Control Volume
Definition:
A specified region in space used to analyze fluid flow, often bounded by a control surface through which mass and momentum can enter or leave.
-
Term: Incompressible Flow
Definition:
Flow in which the fluid density is assumed constant.
-
Term: Steady Flow
Definition:
Fluid flow in which the velocity of the fluid at any given point does not change over time.
-
Term: Turbulent Flow
Definition:
Flow characterized by chaotic, irregular fluid motion, typically resulting in mixing.
-
Term: Laminar Flow
Definition:
Flow in which the fluid moves in smooth, parallel layers with minimal disruption.