Previous Discussion on Conservation of Mass
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Reynolds Transport Theorem
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will revisit the Reynolds transport theorem. Can anyone tell me what role it plays in fluid mechanics?

It helps us relate the changes in a quantity within a control volume to the flow of that quantity across the control surface.

Correct! The Reynolds transport theorem allows us to derive conservation equations. For mass, it translates to control volume analysis. Can anyone mention the assumptions we often apply?

We often assume the flow is steady or unsteady and whether it is compressible or incompressible.

Exactly! Remember: 'steady or unsteady and compressible or incompressible' are keys to simplifying our equations. This simplification is crucial as it helps us tackle complex fluid problems more easily.
Steady vs Unsteady Flow
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

When we talk about steady and unsteady flows, why is this distinction important?

I think steady flow means the fluid properties at any given point do not change over time.

And unsteady flow means those properties can change—right?

Exactly! In steady flow, we can eliminate time derivatives in our equations, simplifying the analysis immensely. This is particularly useful in real-world applications.

So, does that mean most engineering problems can often assume steady flow?

That's right! In many cases, especially in flow devices, we can assume steady, incompressible flow to simplify our calculations.
Application of Conservation of Mass
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's dive into how we apply the conservation of mass in practical problems. What's the general approach?

We should look at the inflow and outflow in a control volume and apply the conservation principle accordingly.

Correct! In applications such as flow through tanks or pipes, we quantify inflow and outflow before we can find storage changes within the volume. What’s an example of a problem we might encounter?

Maybe calculating how much water flows out of a tank when we know the flow rates into and out of it.

Great example! This is vital in various engineering issues related to water supply, fluid transportation, and environmental management.
Setting the Stage for Momentum Conservation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Having covered conservation of mass, who can tell me why understanding this concept is crucial before we move onto conservation of momentum?

Because momentum conservation builds directly upon mass conservation principles.

Exactly right! When analyzing momentum in a system, mass flow rates become integral to understanding changes in momentum. Thus, a solid grasp of mass conservation helps ease into the next section.

Will we also be discussing how to apply these principles in real scenarios?

Yes! We will look at real-world applications of momentum conservation similarly to what we've done with mass.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section reviews the principles of conservation of mass in fluid mechanics, particularly through the Reynolds transport theorem. It discusses the simplifications in steady and incompressible flow, preparing the groundwork for transitioning into the conservation of momentum.
Detailed
In fluid mechanics, the conservation of mass is integral to understanding fluid flow. This section emphasizes the Reynolds transport theorem as a pivotal element for analyzing control volumes. It notes that fluid motion can be classified as steady or unsteady and compressible or incompressible, resulting in corresponding simplifications. When dealing with steady and incompressible flow, the equations can be significantly simplified, often leading to easier problem-solving scenarios. The section ultimately lays the groundwork for extending these principles to the conservation of momentum, which will be further explored. By understanding these foundational concepts, students set the stage for more complex discussions on fluid dynamics, including how mass and momentum interact within flowing systems.
Youtube Videos



![Conservation of mass (a.k.a., continuity) [Fluid Mechanics #2]](https://img.youtube.com/vi/PFgiW7P6omE/mqdefault.jpg)


![The Concept of Conservation of Mass [Fluid Mechanics]](https://img.youtube.com/vi/kBW9pTFYc90/mqdefault.jpg)


Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of Previous Discussions
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Welcome all of you to fluid mechanics course. Today, I am going to deliver lecture on conservation of momentum. As you know, in the last class we discussed about conservation of mass. Also, we have solved few problems based on the conservation of mass.
Detailed Explanation
In the starting of the lecture, the professor sets the context for the current lesson on conservation of momentum by referencing the previous class where the conservation of mass was discussed. This implies that understanding mass conservation is crucial for grasping momentum conservation, as both are fundamental principles in fluid mechanics.
Examples & Analogies
Imagine a water balloon being thrown. Just before it hits the ground, the mass of the water inside is conserved (it doesn't disappear). However, when it bursts upon impact, the momentum also changes, in that the direction and speed of the splashing water molecules become very different. This analogy illustrates how mass conservation sets the groundwork for understanding momentum.
Reynolds Transport Theorem
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
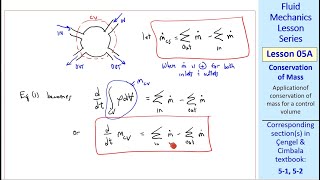
Basically, we have been following the Reynolds transport theorem as a basic concept to apply the setup of the system into physical equations to the control volume level. And, then, at the control column level, we have approximation of extensive and intensive properties and as of now we have derived mass conservation equations.
Detailed Explanation
The Reynolds transport theorem is a vital theorem in fluid mechanics that enables the transition from a control mass perspective to a control volume perspective. It helps in formulating equations that describe the conservation of mass for a fluid that is flowing in and out of a volume of interest, which allows for more practical applications in engineering.
Examples & Analogies
Think of the Reynolds transport theorem as a way to track water going in and out of a bathtub. If you measure how much water you poured in and how much is draining out, you can maintain the balance to understand how full the tub is at any time, just as the theorem helps quantify mass in a flow system.
Key Assumptions in Conservation of Mass
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
we have two basic assumptions, that is, with respect to time is it a steady or unsteady. So, the steady we do the approximations of many fluid flow problems which are steady problems. Then, with respect to density change or the variations of the density, we divide it, flow is compressible or incompressible.
Detailed Explanation
When applying conservation of mass, it's crucial to determine whether the fluid conditions are steady or unsteady. A steady flow means that the fluid's velocity and other properties don’t change over time, while unsteady flow means they do. Additionally, fluids can sometimes compress (like gases) or remain incompressible (like liquids), which impacts how we apply mass conservation equations.
Examples & Analogies
Consider traffic on a highway: in a steady state, cars continue to fill lanes without speed changes (like water in a pipe), but if a road construction starts, the flow becomes unsteady. Similarly, if some cars are compact and others are larger trucks, this mimics compressible vs. incompressible flow encounters.
Application of Reynolds Transport Theorem
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
So, when you have the steady assumptions, you can remember that the component of Reynolds transport theorem of time, differentiate components become 0 or the volume integral component part of the Reynolds transport theorem becomes 0.
Detailed Explanation
In situations where steady flow conditions are assumed, certain terms in the Reynolds transport theorem can be simplified to zero, making calculations more manageable. This allows engineers to focus on surface integrals, which are necessary for practical applications without the complexity of changing properties over time.
Examples & Analogies
This can be related to how a factory runs efficiently when all machines work at a constant speed without interruptions, leading to predictability. When everything is steady, calculations are simplified just like understanding the production flow becomes easier.
Understanding Flow Dynamics in Control Volumes
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Thus, the problems become too simple as compared to if you have compressible flow. So, when you have a steady incompressible flow, most of the cases what we consider for flow devices or engineering applications, we can consider steady incompressible flow, then the problems become very simplified when you apply for Reynolds transport theorem.
Detailed Explanation
In many engineering scenarios, the steady incompressible flow condition is a common assumption because it greatly simplifies the mathematics involved. By considering the density of the fluid constant, it reduces the number of variables that need to be accounted for in calculations.
Examples & Analogies
Imagine using a flexible straw to drink juice. If the juice doesn't change and flows steadily, it's easier to drink and calculate how much you've had, similar to working with constant density. However, if bubbles appear, and foam starts, the dynamics of flow become more complicated, like considering compressible flows.
Key Concepts
-
Reynolds Transport Theorem: A fundamental principle for deriving conservation equations in fluid mechanics.
-
Conservation of Mass: Essential for analyzing fluid dynamics, stating that mass is conserved within a control volume.
-
Steady vs Unsteady Flow: Important classifications for simplifying analysis and calculations in fluid mechanics.
-
Control Volume: A crucial concept for applying conservation laws in practical scenarios.
Examples & Applications
Calculating water flow in a tank with given inflow and outflow rates.
Estimating seepage losses in a soil matrix using conservation of mass principles.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a closed system, mass stays the same, it’s a conservation game!
Stories
Imagine a sealed box where water flows in and out, but its total weight remains unchanged. This shows how mass conservation works.
Acronyms
For the four principles
Control
Flow
Steady
Mass - just remember 'CFSM' to keep it clear.
SICS (steady, incompressible, control volume, system) helps remember key characteristics of analysis.
Flash Cards
Glossary
- Conservation of Mass
A principle stating that mass cannot be created or destroyed in a closed system.
- Reynolds Transport Theorem
A theorem that relates the change of a quantity within a control volume to the flow across its boundaries.
- Steady Flow
A flow condition in which fluid properties at a specific point do not change over time.
- Unsteady Flow
A flow condition where fluid properties at a specific point do change over time.
- Control Volume
A fixed region in space through which fluid flows, used for analysis in fluid mechanics.
- Incompressible Flow
Flow where the fluid density remains constant.
Reference links
Supplementary resources to enhance your learning experience.
