Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to the Reynolds Transport Theorem
Unlock Audio Lesson
Today, we're going to dive into the Reynolds Transport Theorem. This theorem is essential for understanding how properties of fluids change when they flow in and out of a control volume. Can anyone tell me what a control volume is?
Isn’t it just a specific area where we analyze fluid flow?
Exactly! When we say a control volume, we're referring to a designated region in space where we can observe how fluids behave. Now, why do we need the Reynolds Transport Theorem, and what does it help us with?
I think it's about connecting the amount of fluid flowing in and out?
That's correct, Student_2! RTT helps us connect the rate of change of a property within the control volume to the flow of that property across its boundaries. Remember the acronym ‘RTT’ for Reynolds Transport Theorem!
Application of the Theorem
Unlock Audio Lesson
Now that we understand RTT, let’s discuss its application in deriving the conservation of mass equation. Can someone summarize how we apply steady flow conditions?
In steady flow, properties don’t change with time, so we can simplify our calculations!
Exactly! This simplification means that we can focus on the flow across the surface boundaries without worrying about changes over time. Additionally, we classify flows based on compressibility – can anyone explain this classification?
It's about whether density changes or remains constant, right? Like compressible flows where density varies and incompressible where it does not.
Perfect! Remember that RTT is vital for both compressible and incompressible flows, making it widely applicable!
Conservation of Momentum
Unlock Audio Lesson
Next, let's apply RTT to the conservation of momentum. Why do you think momentum conservation is crucial in fluid dynamics?
Because it helps us understand how forces act on fluids and their resulting motion?
Precisely! The conservation of momentum relates to how the forces acting on a fluid element can describe its motion. So, when we apply RTT to derive the momentum equations, we consider body forces and surface forces. Can anyone name a type of body force?
Gravity?
Correct! Gravity is a primary body force acting on fluids. Let's make sure we understand the difference between body and surface forces, as they'll come up frequently when we analyze fluid situations.
Real-World Applications
Unlock Audio Lesson
Now, let’s think about the real-world applications of RTT. Can anyone think of an example where it's applied in engineering?
Hydropower projects? Like the Bhakra Nangal project?
Great example, Student_3! Such projects rely heavily on fluid mechanics principles, including RTT. How does understanding these principles affect the design and efficiency of such projects?
It helps in estimating power potentials and designing turbines, which is crucial for efficiency!
Exactly right! Understanding the behavior of fluids through RTT allows engineers to optimize design processes and enhance overall efficacy.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we delve into the Reynolds Transport Theorem, which serves as a foundational principle in fluid mechanics. It encapsulates the relationship between a fluid's properties and their changes over time, applying to both fixed and moving control volumes, and lays the groundwork for deriving equations of conservation of mass and momentum.
Detailed
Detailed Summary of Reynolds Transport Theorem
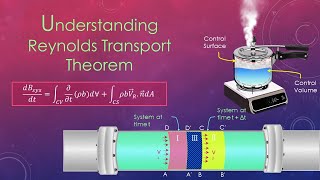
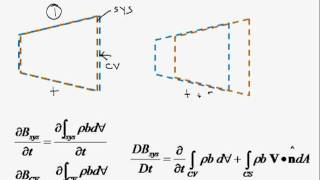
The Reynolds Transport Theorem (RTT) is a pivotal concept in fluid mechanics that helps in understanding how various physical quantities (like mass and momentum) change within a control volume. The theorem relates the time rate of change of an extensive property of a system to the flow of that property across the control volume's boundaries.
Key Concepts of RTT:
- Control Volume: A defined region in space where fluid flow is analyzed, which can be fixed in space or moving.
- Extensive vs Intensive Properties: Extensive properties such as mass and momentum depend on the amount of substance, while intensive properties like density remain constant regardless of the volume.
- Conservation Laws: The RTT is foundational to both conservation of mass and momentum principles, providing the mathematical framework to derive these laws.
- Steady vs Unsteady Flow: The application of RTT varies based on flow conditions; in steady flow, properties do not change over time, simplifying the calculations significantly.
The application of RTT leads to equations that engineers and scientists use to solve real-world problems involving fluids, making it a critical tool in civil engineering and various fluid applications. By understanding RTT, students can approach complex fluid mechanics problems with a solid theoretical foundation.
Youtube Videos
![Get to know Reynolds Transport Theorem - part I [Fluid Mechanics]](https://img.youtube.com/vi/BwOnHIsgK_Q/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Overview of the Reynolds Transport Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Basically, we have been following the Reynolds transport theorem as a basic concept to apply the setup of the system into physical equations to the control volume level. And then, at the control column level, we have an approximation of extensive and intensive properties, and as of now, we have derived mass conservation equations.
Detailed Explanation
The Reynolds Transport Theorem is a fundamental principle used in fluid mechanics. It allows us to relate the macroscopic behavior of fluid systems described by control volumes to the flow of individual fluid particles. It provides a framework for converting between the total derivative of a quantity and the integral form, allowing us to apply conservation laws effectively for mass or momentum. This theorem helps us to derive equations that model physical phenomena in engineering, particularly in fluid dynamics.
Examples & Analogies
Imagine you are trying to capture the flow of water in a river using a large bucket (the control volume). The Reynolds Transport Theorem helps you to know how much water is entering and leaving the bucket over time, allowing you to understand the behavior of the water flow around it.
Key Assumptions: Steady vs. Unsteady Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As I told you, we discussed about the Reynolds transport theorem for conservation of mass, and when we apply this conservation of mass to the Reynolds transport theorem, we have two basic assumptions, that is, with respect to time is it a steady or unsteady.
Detailed Explanation
In fluid mechanics, flows can be categorized as 'steady' or 'unsteady'. Steady flow implies that properties at any point in the fluid do not change over time. In contrast, in unsteady flow, these properties do change. When analyzing a system using the Reynolds Transport Theorem, identifying whether a flow is steady or unsteady helps in selecting the right mathematical approach; for steady flow, specific simplifications can be made, leading to easier calculations.
Examples & Analogies
Consider a garden hose. If you keep the nozzle open until the hose is empty, that would be steady flow—the amount of water flowing out remains constant. If you periodically cover and uncover the nozzle, changing the flow rate, that's unsteady flow— the water flow varies over time.
Compressible vs. Incompressible Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Then, with respect to density change or the variations of the density, we divide it, flow is compressible or incompressible.
Detailed Explanation
Fluid flows can also be categorized based on the compressibility of the fluid. Compressible flow occurs when changes in density are significant, notably in gases at high speeds, whereas incompressible flow assumes constant density, applicable primarily to liquids under many practical conditions. Understanding whether a flow is compressible or incompressible affects how equations are formulated, as this greatly influences the behavior of the fluid as it moves through a system.
Examples & Analogies
Imagine blowing up a balloon. The air inside the balloon is compressible; as you blow more air in, the density of the air changes because it gets packed into a smaller volume. In contrast, think about a water balloon; when you fill it with water, the water's density hardly changes regardless of how much more water you add—this is analogous to incompressible flow.
Simplifying Assumptions for Steady Incompressible Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
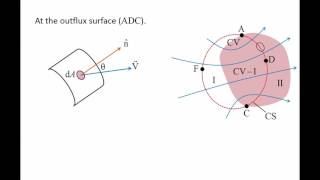
So, when you have the steady assumptions, you can remember that the component of Reynolds transport theorem of time, differentiate components become 0 or the volume integral component part of the Reynolds transport theorem becomes 0.
Detailed Explanation
Under the assumption of steady and incompressible flow, the time-based components of the Reynolds Transport Theorem simplify significantly. The volume integral of changes over time becomes zero, which means that we only need to consider the boundary conditions (surface integrals). This greatly simplifies our calculations and leads to straightforward relationships between velocities and areas.
Examples & Analogies
This is like focusing only on the amount of water flowing out of a stationary water tank through a pipe, ignoring any changes in flow over time; you only care about how much water flows out at a given moment, making it easier to measure and calculate.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Control Volume: A defined region in space where fluid flow is analyzed, which can be fixed in space or moving.
-
Extensive vs Intensive Properties: Extensive properties such as mass and momentum depend on the amount of substance, while intensive properties like density remain constant regardless of the volume.
-
Conservation Laws: The RTT is foundational to both conservation of mass and momentum principles, providing the mathematical framework to derive these laws.
-
Steady vs Unsteady Flow: The application of RTT varies based on flow conditions; in steady flow, properties do not change over time, simplifying the calculations significantly.
-
The application of RTT leads to equations that engineers and scientists use to solve real-world problems involving fluids, making it a critical tool in civil engineering and various fluid applications. By understanding RTT, students can approach complex fluid mechanics problems with a solid theoretical foundation.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An example of applying RTT is estimating the flow rate of water through a pipe by analyzing the inflows and outflows across the control volume.
-
In civil engineering, RTT can be utilized to analyze sediment transport in river systems.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a control volume, fluids flow, properties change when speeds do grow.
📖 Fascinating Stories
-
Imagine a dam where water is trapped; it’s like a control volume where flow is mapped.
🧠 Other Memory Gems
-
R = Relationship of flow, T = Time rate of change, T = Through the boundary.
🎯 Super Acronyms
RTT
- R: for Rate
- T: for Transport
- T: for Theorem.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Control Volume
Definition:
A specified region in space through which fluid can flow, used for analyzing fluid dynamics.
-
Term: Extensive Property
Definition:
A property that depends on the amount of material in the system, such as mass or volume.
-
Term: Intensive Property
Definition:
A property independent of the amount of material, such as temperature or density.
-
Term: Conservation of Mass
Definition:
A principle that states mass cannot be created or destroyed in an isolated system.
-
Term: Momentum
Definition:
The quantity of motion of a moving body, measured as a product of its mass and velocity.