Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Steady vs Unsteady Flow
Unlock Audio Lesson
Today we're going to differentiate between steady and unsteady flow. Who can explain what steady flow means?
Steady flow means the velocity at any point in the fluid does not change over time.
Exactly! In steady flow, properties like velocity and pressure remain constant at any given point. Now, what about unsteady flow?
In unsteady flow, the properties change with time.
Correct! Unsteady flow can complicate our calculations, especially when using the Reynolds transport theorem, which becomes more complex due to time derivatives.
So, are most engineering applications primarily steady?
Generally, yes. Many systems are designed assuming steady, incompressible flow which simplifies the governing equations significantly.
To remember this distinction, think of 'steady' as 'same over time.' Now let's summarize what we've learned today.
So, in summary, steady flow means no change over time, while unsteady flow indicates change, greatly affecting our calculations in fluid dynamics.
Applications of Steady vs Unsteady Flow
Unlock Audio Lesson
Now, let's discuss practical applications. Why is it important to understand steady versus unsteady flow in design projects?
It helps engineers predict how fluids will move, which is crucial for designing effective hydraulic systems.
Great point! For instance, in reservoirs, knowing the flow type can influence how we manage water seepage. What happens if we misinterpret the flow type?
We might underestimate or overestimate the necessary structures or systems to handle water flow!
Exactly! Miscalculations can lead to disastrous failures. Can someone give an example of steady flow in engineering?
A consistent outflow from a dam would be a steady flow situation.
Right! Now, let's remember that steady flow allows for simplified calculations, while unsteady flow involves more complexity.
To wrap up, understanding these concepts aids significantly in effective engineering practices, ensuring safety and efficiency.
The Reynolds Transport Theorem in Context
Unlock Audio Lesson
Let's connect our discussion to the Reynolds transport theorem. How does understanding flow types help when applying this theorem?
For steady flow, we can simplify our equations because the time derivatives become zero.
Exactly! And what does this mean for our computations?
It makes them significantly easier, as we only focus on surface integrals.
Correct! With unsteady flow, our equations remain complex with time dependencies. Hence, accurate assessment is crucial.
Without proper understanding, we might get incorrect results.
Absolutely! A strong grasp of these concepts impacts the reliability of our predictions.
In summary, knowing flow types allows us to apply the Reynolds transport theorem effectively, ensuring our analysis is accurate.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In fluid mechanics, understanding the difference between steady and unsteady flow is crucial for applying equations governing fluid behaviors. Steady flow implies constant velocity at any point over time, while unsteady flow varies with time. This section elaborates on how these concepts influence the conservation laws, particularly in real-world applications such as in hydraulic systems.
Detailed
Steady vs Unsteady Flow
Overview
In fluid mechanics, flow classification into steady and unsteady states plays a critical role in understanding and applying various conservation laws, particularly through the Reynolds transport theorem.
Steady Flow
- Definition: A flow is considered steady if the fluid properties at any point do not change with time.
- Implications: In steady flow, simplifications can be made in calculations, as time derivatives in the Reynolds transport theorem become zero, making it easier to analyze systems where fluid behavior is predictable and constant.
Unsteady Flow
- Definition: In contrast, unsteady flow is characterized by changes in fluid properties at any point over time.
- Implications: The complexity of calculations increases as time derivatives remain in the governing equations, necessitating more rigorous analysis to account for these variations.
Practical Applications
Understanding whether a flow is steady or unsteady aids in the design of various hydraulic systems and computational models, impacting everything from reservoir management to infrastructure design in civil engineering. Examples such as the analysis of seepage in soil structures highlight the practical importance of these concepts.
In summary, distinguishing between steady and unsteady flow is fundamental for engineers to make accurate predictions and designs in fluid-related systems.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Steady and Unsteady Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Basically, we have been following the Reynolds transport theorem as a basic concept to apply the setup of the system into physical equations to the control volume level. And, then, at the control column level, we have approximation of extensive and intensive properties and as of now we have derived mass conservation equations. Today, I am going to derive conservation of linear momentum.
Detailed Explanation
In fluid mechanics, flow can be classified as steady or unsteady. A steady flow means that the fluid's velocity at a given point does not change with time. In contrast, in an unsteady flow, the fluid velocity at a given point changes over time. The Reynolds transport theorem helps in analyzing these flows by allowing us to set up equations for control volumes that consider both mass and momentum conservation.
Examples & Analogies
Think about a garden hose. If you have the water flowing steadily without changing the speed, that's like a steady flow. But if you were to turn the tap on and off, causing the water speed to change, that would be an example of unsteady flow.
Understanding Steady and Unsteady Assumptions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
As I told you, we discussed about the Reynolds transport theorem for conservation of mass and when we apply this conservation of mass to the Reynolds transport theorem, we have two basic assumptions: with respect to time is it steady or unsteady.
Detailed Explanation
The first step in applying the Reynolds transport theorem is to identify whether the flow is steady or unsteady. If the flow is steady, we can simplify our calculations considerably. In steady flow, properties such as fluid velocity and density do not change with time, allowing us to focus on surface integrals rather than time-dependent factors. This simplifies our equations significantly.
Examples & Analogies
Imagine driving down a highway at a constant speed. That’s like steady flow; your speed remains unchanged. Now, think about driving through traffic, where you constantly start and stop. That's akin to unsteady flow as your speed varies frequently.
Characteristics of Steady Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, when you have the steady assumptions, you can remember that the component of Reynolds transport theorem of time, differentiate components become 0 or the volume integral component part of the Reynolds transport theorem becomes 0.
Detailed Explanation
In steady flow situations, the time derivatives of flow properties average out to zero because nothing changes as time progresses. This means the volume integral of the Reynolds transport theorem can also be simplified. In practical terms, this makes it easier to focus solely on the surface integrals, which directly relate to the flow of fluid across the boundary of the control volume.
Examples & Analogies
If you think about filling a bathtub with water at a constant rate, the water level rises steadily without fluctuating. This is similar to a steady flow where the rate of water entering equals the rate of water in the tub, resulting in no change in water level over time.
Incompressible vs Compressible Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Then, with respect to density change or the variations of the density, we divide it, flow is compressible or incompressible. So, we can have two types of approximations, steady compressible, steady incompressible.
Detailed Explanation
Fluid flows can be further classified as compressible or incompressible based on how much the fluid’s density changes during flow. For incompressible flows (like water), density changes are negligible. For compressible flows (like gases), density can change significantly. Understanding whether the flow is compressible or not is crucial for applying appropriate equations and assumptions.
Examples & Analogies
Think about a balloon. When you blow air into it, you compress the air, making it a compressible flow. Now, consider water flowing through a pipe. The density of the water remains almost constant, representing an incompressible flow.
Applications of Steady Incompressible Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So, when you have a steady incompressible flow, most of the case what we consider for flow devices or engineering applications, we can consider steady incompressible flow, then the problems become very simplified when you apply for Reynolds transport theorem.
Detailed Explanation
In engineering applications, most flows we deal with can be approximated as steady and incompressible. This significantly simplifies calculations because we can assume constant density and streamline the equations we use to analyze the flow. This makes it easier to predict outcomes in systems such as piping, open channels, and many mechanical devices.
Examples & Analogies
Consider a simple faucet. When you turn it on, the flow of water is steady and behaves as incompressible fluid. Engineers can predict how much water will flow out based on the size of the faucet and the pressure in the pipes without considering complex changes in density.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Steady Flow: Refers to a fluid that maintains constant properties over time at any point in space.
-
Unsteady Flow: Refers to variations in fluid properties with time at any point.
-
Reynolds Transport Theorem: A theorem that enables analysis of changes in fluid quantities considering control volumes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
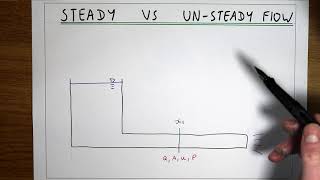
In a river where the flow speed remains constant, we have steady flow.
-
During a rainstorm, the flow of water in a drainage system may change, characterizing it as unsteady flow.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Steady flow, like a river, goes straight; Unsteady flow changes its fate.
📖 Fascinating Stories
-
Imagine a calm lake – that is steady flow, while a stormy river full of twists is unsteady.
🧠 Other Memory Gems
-
For steady flow, think 'SSS' – Same Speed Steady; for unsteady, 'UUU' – Unpredictably Unstable.
🎯 Super Acronyms
MEMO – Remember Steady flow as M-Maintains E-Everything M-Motions O-Ordinary.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Steady Flow
Definition:
A flow condition where the fluid properties at a given point do not change with time.
-
Term: Unsteady Flow
Definition:
A flow condition where fluid properties do change with time.
-
Term: Reynolds Transport Theorem
Definition:
A fundamental theorem that provides a framework for analyzing fluid motion, relating the change in a quantity over time to the flow of that quantity across a control surface.