Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Reynolds Transport Theorem
Unlock Audio Lesson
Today, we'll start with Reynolds Transport Theorem, an essential principle in fluid mechanics. Can anyone explain what it connects in our fluid studies?
It helps link the properties of a fluid system to a control volume around it, right?
Exactly! It helps us apply conservation laws to a specified volume of fluid. Remember, Reynolds Transport Theorem is crucial for analyzing changes over a defined volume.
Can we simplify it for certain cases, like steady flow?
Yes, good point! When we assume steady flow, we eliminate time-dependent terms, simplifying our calculations significantly.
What about density? Does that affect our approach?
Absolutely! Fluid density affects our classification into compressible or incompressible flows. Keeping these distinctions in mind is crucial!
To summarize, we connect fluid behaviors to a control volume using Reynolds Transport Theorem, simplifying our equations in steady and incompressible flows.
Conservation of Mass
Unlock Audio Lesson
Let's discuss conservation of mass. How does it apply to our previous examples?
In one example, we looked at fluid entering and exiting a control volume to show mass balance.
Yes! Mass inflows must equal mass outflows in a steady-state condition. Can anyone define what a control volume is?
It's a fixed or moving region where we analyze mass and energy changes.
Spot on! And how do we mathematically express conservation of mass in a control volume?
We set up an equation where inflows minus outflows equals any change in mass within the control volume.
"Correct! Let's remember the continuity equation
Conservation of Momentum
Unlock Audio Lesson
Now, shifting gears to the conservation of momentum. How does it relate to our control volume concept?
It determines how the momentum changes within a control volume based on the forces acting on it.
Well articulated! Can you explain what we mean by body forces and surface forces in this context?
Body forces act throughout the volume, like gravity, while surface forces come from pressures and shear on the boundary.
Exactly! When we derive momentum equations, we consider both forces. Can anyone summarize the essential steps?
We model the control volume, apply Newton's laws to it, and account for all forces acting on it.
Right! Remember, our momentum equations incorporate these forces, balancing them with inertia from fluid movement.
To wrap up this section, always remember: understanding how momentum interacts with a control volume is key to many fluid mechanics applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
This section delves into the Control Volume Approach within fluid mechanics, focusing on the conservation of mass and linear momentum. It discusses the Reynolds Transport Theorem, assumptions for steady and unsteady flows, compressible and incompressible flows, and the simplifications applied when analyzing flow problems. Various examples illustrate the practical application of these concepts.
Detailed
Control Volume Approach in Fluid Mechanics
The Control Volume Approach is a fundamental principle in fluid mechanics that facilitates the analysis of fluid flow through a designated volume of space (the control volume) by applying the conservation of mass and momentum principles. This discussion begins with a recap of the Reynolds Transport Theorem, which provides a link between the system's behavior and its control volume's modeling.
Key assumptions in applying the Control Volume Approach include the terminology of steady vs. unsteady flow, and the classification of density as compressible or incompressible. For steady flows, the time derivative components of the Reynolds Transport Theorem can be simplified to yield manageable equation forms.
The section also details the process of deriving the momentum equations for fixed and moving control volumes and discusses relevant simplifications such as neglecting atmospheric pressure and applying the momentum flux correction factor. Our exploration includes practical examples like the conservation of mass in porous media and analysis of flow through pipelines, reinforcing the utility of the control volume framework in engineering applications.
Overall, this section underscores the significance of understanding fluid behavior through the control volume approach, serving as a cornerstone for further studies in fluid dynamics.
Youtube Videos
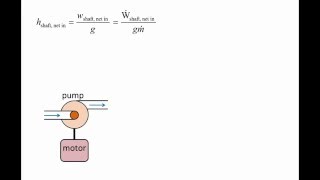
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Control Volume Approach
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Basically, we have been following the Reynolds transport theorem as a basic concept to apply the setup of the system into physical equations to the control volume level.
Detailed Explanation
The control volume approach involves using the Reynolds transport theorem, which helps in translating the physical behavior of a fluid system into mathematical equations. This theorem relates the rate of change of an extensive property (like mass or momentum) in a control volume to the flow of that property across the control surfaces. By applying this theorem, we can analyze the fluid flow characteristics within a defined region in space.
Examples & Analogies
Imagine a swimming pool (the control volume) where you add and remove water (the mass). The Reynolds transport theorem helps you understand how the water level changes in the pool based on the amount you pour in or drain out.
Assumptions in Control Volume Analysis
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
we have two basic assumptions, that is, with respect to time is it a steady or unsteady.
Detailed Explanation
In control volume analysis, the flow situation can either be steady or unsteady. A steady flow means that the properties of the fluid (like velocity, density) at any point do not change over time. In contrast, an unsteady flow implies that these properties can change with time. Understanding the nature of flow is crucial as it influences how we apply equations and calculate various properties.
Examples & Analogies
Think of a garden hose. If you turn the nozzle and keep the water flow constant, you have steady flow. But if you turn it on and off or fluctuate the pressure, you create unsteady flow, changing how much water comes out and at what speed.
Types of Fluid Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
we can have two types of approximations, steady compressible, steady incompressible.
Detailed Explanation
Fluid flow can also be classified based on the compressibility of the fluid. Compressible flows involve significant changes in fluid density, often seen in gases, especially at high velocities. Incontrast, incompressible flows assume constant fluid density, which is typically valid for liquids at relatively low speeds. In many engineering applications, especially involving water flow in pipes, we often assume incompressible flow for simplification.
Examples & Analogies
This is like comparing how you fill a balloon (compressible) versus a cup of water (incompressible). The balloon can change size (and density) when you blow into it, while the cup remains at the same level no matter how you pour water into it.
Simplifications for Steady Incompressible Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
when you have a steady incompressible flow, most of the case what we consider for flow devices or engineering applications.
Detailed Explanation
When applying the control volume approach in steady incompressible flow scenarios, many terms in the Reynolds transport theorem simplify significantly. The time derivatives of properties become zero, making the calculations easier. Analysts can focus primarily on the area integral components associated with fluid entering or exiting the control volume, which simplifies solving flow problems for practical engineering applications.
Examples & Analogies
Imagine you are measuring the water entering and leaving a bathtub while everything else remains constant. You can easily notice that as you pour water in (steady), it fills up without any sudden drops or increases in the level (incompressible). This makes it simple to predict how long it will take to fill the tub.
Application of Control Volume Approach in Practical Scenarios
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
we have discussed various examples where applying the control volume approach effectively resolves problems.
Detailed Explanation
The control volume approach is not just theoretical; it has many practical applications in fields like civil engineering, mechanical engineering, and hydrology. By using this approach, engineers can model systems accurately, design efficient flow devices like pumps and turbines, and assess environmental impacts. For example, determining how water flows through a channel using control volume principles can help in designing effective drainage systems.
Examples & Analogies
Envision a water treatment facility where scientists must ensure clean water flows out at the right rate. They use the control volume method to monitor water intake and outflow, making adjustments as needed to guarantee clean water while avoiding contamination.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Reynolds Transport Theorem: Connects system and control volume analyses.
-
Conservation of Mass: Ensures that mass inflow equals outflow in a control volume under steady flow.
-
Conservation of Momentum: Balances the forces acting on a control volume to describe momentum changes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Analyzing a tank with multiple inlets and one outlet to apply conservation of mass.
-
Applying momentum equations to a fixed control volume around a jet flowing from a pipe.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluids we flow, mass must not cease, In a control space, it finds its peace.
📖 Fascinating Stories
-
Imagine water flowing from a tap into a bowl. The bowl can't overflow if the tap and drain balance, representing conservation principles.
🧠 Other Memory Gems
-
Remember the acronym 'COMET': Conservation of Mass, Energy, and Momentum Equals Total changes.
🎯 Super Acronyms
Use the acronym 'TRASH' - Time, Reynolds, Area, Steady, and Hydrodynamics to recall key components of fluid mechanics analysis.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Control Volume
Definition:
A defined volume in space through which fluid flows, considered for analysis in fluid dynamics.
-
Term: Reynolds Transport Theorem
Definition:
A theorem that relates the rate of change of a quantity in a control volume to surface integrals across its boundary.
-
Term: Steady Flow
Definition:
Fluid flow characteristics that do not change with time.
-
Term: Incompressible Flow
Definition:
Flow where the fluid density remains constant throughout.
-
Term: Body Force
Definition:
A force acting throughout the volume of a fluid, such as gravity.
-
Term: Surface Force
Definition:
Forces that act on the boundary of a control volume, including pressure and viscous forces.