Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Radius of Gyration
Unlock Audio Lesson
Today we're diving into the concept of radius of gyration. This term typically describes how the mass is distributed relative to an axis. Can anyone share what they think this might relate to in fluid mechanics?
Does it have to do with how a fluid behaves in motion, like when it's inside a shipping container?
Great insight! The radius of gyration is essential in determining stability, especially in ships. The greater the radius, the more stable the ship is under rolling conditions. Remember, stability is linked to the mass distribution. One way to think about this is 'greater distance, greater stability.'
So, does it mean a ship with a larger radius of gyration will be harder to tip over?
Exactly! A larger radius indicates that mass is spread further from the center, providing better stability. Let's use 'R.G. for stability' as a mnemonic to remember this fact.
Can we calculate how much more stable it makes the ship?
Yes, exactly! We can calculate the radius of gyration and relate that to the period of rolling or metacentric height. Let's discuss these calculations.
To summarize, the radius of gyration affects stability – larger means greater stability. Remember 'R.G. for stability'.
Equations and Calculations
Unlock Audio Lesson
Now let's look at how we actually calculate the radius of gyration. For a simple case, we take the moment of inertia and relate it to the mass. Does anyone know the formula?
I think it has to do with the mass and the height… something like that?
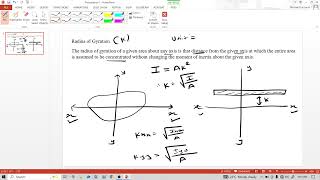
Close! The formula links the radius of gyration (k) to the moment of inertia (I) and mass (m): k² = I/m. It gives us a practical way to see the distribution of mass regarding stability.
So if we increase the height, we could affect the radius of gyration too, right?
Exactly! Increasing mass above the metacenter can impact stability positively or negatively depending on distribution. Who remembers why this matters?
It matters for how a ship handles waves, right?
Absolutely! To wrap up, the radius of gyration is calculated using the equation k² = I/m, which shows us the relationship between moment of inertia and mass—all connected to stability.
Fluid Dynamics Applications
Unlock Audio Lesson
Next, let’s apply what we learned about the radius of gyration to real situations, such as fluid flow in pipelines. How do you think this applies?
Maybe it relates to pressure drops in a pipe as fluids move through?
Yes! Pressure variations within fluid systems are critical, especially where radius of gyration affects flow stability. Can anyone think of an example where this applies?
How about when oil and water are transported through pipelines?
Spot on! Different densities require adjustments in pressure. And remember, this is governed by our understanding of radius of gyration and how it relates to fluid stability. Let’s solidify with a quiz question: What happens if we increase the diameter of a pipeline?
Wouldn’t that decrease the pressure for the same flow rate?
Correct! Increased diameter decreases velocity, affecting pressure. In summary, radius of gyration is integral for real-world fluid dynamics, especially in terms of stability and pressure.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section elaborates on the radius of gyration, its connection to ship stability, and related fluid mechanics principles. It includes the derivations and applications in various scenarios, alongside examples and problems to reinforce learning.
Detailed
Detailed Summary
In this section, we explore the concept of radius of gyration, a crucial parameter in fluid mechanics and ship stability. The radius of gyration is fundamentally linked to the distribution of mass about an axis and plays an essential role in understanding how ships behave under various conditions.
We begin with the equilibrium conditions impacting the radius of gyration, discussing how upward forces due to surface tension balance out downward forces such as the weight of the fluid. Using the relations derived from these balance considerations, we explain the calculations necessary to obtain the radius of gyration. This section also covers the influence of metacentric height and the period of rolling on the stability of ships, incorporating relevant formulas and examples that demonstrate the practical application of concepts like capillary rise and pressure differences. We will also analyze specific problems involving pipelines, fluid conditions, and oscillations to ensure clarity and comprehension of the radius of gyration in fluid dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Upward and Downward Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now I have just equating this since is a equilibrium conditions in the so upward force is equal to the downward force.
Upward force = downward force
(T1 + T2) Cos(θ) * ρ * h * σ(D^2 - d^2)
T1 = ρA1
T2 = ρA2
The upward force is a surface tension force part, that what will act for two different diameters.
Detailed Explanation
In this section, we start by acknowledging that in a fluid system, the upward force exerted by the surface tension must equal the downward force, which is typically the weight of the fluid. This balance creates an equilibrium condition. The upward force is quantified by considering the contributions from the surface tension at the two different diameters of the fluid column. Specifically, if we denote the surface tensions at these diameters as T1 and T2, we can express them using their respective areas and densities. This principle is foundational in fluid mechanics, establishing how forces interact in a fluid system.
Examples & Analogies
Imagine a water strider bug walking on the surface of a pond. It can stay on the surface without sinking because the surface tension of the water supports its weight. Just like how the upward surface tension force counters the bug's weight, in fluid systems, we analyze how forces balance to maintain equilibrium.
Calculating Downward Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we can compute the downward force which is the weight of the fluid. That what we confined by this the capillary rise. That what will be
(ρ * (D + d) Cos(θ) = π * (D + d) * h * σ - π * d * h * σ
That what will give us the weight which is the weight of the fluid acting downwards, the upper part.
Detailed Explanation
Here, we are focusing on calculating the downward forces in the fluid system. The downward force is primarily the weight of the fluid influenced by capillary action. The equation shows how the combined area of the larger and smaller diameters influences the fluid's weight. This means that as we analyze the behavior of the fluid column, we recognize that both the height of the liquid column and the diameters contribute to the forces acting downward.
Examples & Analogies
Think of a straw in a drink. When you suck on one end, you lower the pressure inside the straw, allowing the liquid to rise against gravity through capillary action. The weight of the drink pushes down while the pressure differential created above pulls the liquid upward, similar to how we balance forces in our calculations.
Deriving Relationships Between Variables
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So if I just rearrange these terms the finally, I will get this ones.
That is what very basic way I will get it the relations between the capillarity height angle of contact and these two are the diameter of annular systems where you will have a and sigma stands for surface tensions.
Detailed Explanation
In this part, we rearrange the equations to derive the relationships among various fluid parameters, such as capillary height, contact angle, and the diameters of the system. This logical restructuring helps us understand how alterations in one variable can affect the others. Recognizing these relationships is crucial in fluid dynamics as they allow us to make predictions about system behavior under varying conditions.
Examples & Analogies
Imagine adjusting a garden hose's nozzle. If you change the diameter of the nozzle, it will affect the flow's height and pattern of the water spraying out, much like how changing the diameters of a fluid system affects the capillary action and height of the liquid.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Radius of Gyration: A crucial parameter for understanding the distribution of mass affecting fluid stability.
-
Metacentric Height: Indicates how stable a floating body is based on the height of its center of mass above its metacenter.
-
Moment of Inertia: Essential for calculating radius of gyration, determining how mass + height influence stability.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When analyzing a ship's performance in rough seas, the radius of gyration can help predict how stable the vessel will be during waves.
-
In designing pipelines, understanding the radius of gyration can aid in ensuring that fluids flow evenly without creating adverse pressure drops.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To keep your ship upright and steady, keep mass spread out, and then you're ready!
📖 Fascinating Stories
-
Imagine a ship sailing across a stormy sea. A tall mast makes it vulnerable, while a wide hull keeps it steady. The radius of gyration is like a ship's arm, reaching out to help it stay upright.
🧠 Other Memory Gems
-
Use 'R-G-Stability' to recall that Radius of Gyration relates to ship Stability!
🎯 Super Acronyms
RGS - Remember Gyration for Stability.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Radius of Gyration
Definition:
A measure of how mass is distributed relative to an axis, impacting stability in fluid dynamics.
-
Term: Stability
Definition:
The ability of a ship or floating body to return to its upright position after being tilted.
-
Term: Moment of Inertia
Definition:
A measure of an object's resistance to changes in its rotation rate, critical in determining radius of gyration.
-
Term: Metacentric Height
Definition:
The vertical distance between the center of gravity and the metacenter of a floating body, indicating stability.