Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Metacentric Height
Unlock Audio Lesson
Today, we'll discuss the importance of metacentric height in maintaining a ship's stability. Can anyone tell me what metacentric height is?
Is it the distance from the center of gravity to the metacenter?
Exactly! The metacentric height, GM, plays a crucial role in stability. Why do you think that is important?
I think it's important because it affects how quickly a ship can right itself after tilting.
Great point! Remember, higher GM means increased stability. An easy way to remember is GM = Great Maneuverability!
What happens if GM is low?
Good question! A low GM can cause the ship to be unstable and lead to capsizing, especially in rough seas.
Rolling Period of Ships
Unlock Audio Lesson
Next, let's discuss the period of rolling, which is how long it takes for the ship to complete one full roll back to equilibrium. The formula to calculate it is T = 2π√(GM/g). Who can explain the terms in this formula?
T is the period, GM is the metacentric height, and g is the gravity!
Absolutely right! Now, how would we find the radius of gyration from the given data of GM and T?
We can rearrange the formula to solve for GM.
Yes! If we know the metacentric height and the period of rolling, we can find the relevant radius of gyration. This relationship is vital for ship stability analysis.
Applications and Implications
Unlock Audio Lesson
Now we'll talk about the implications of metacentric height in real-world applications. Why do you think ship designers place emphasis on this aspect?
It's to ensure that ships remain stable in bad weather!
Exactly! Stability is critical for reducing the risk of capsizing. Can anyone think of situations where low GM might be dangerous?
In stormy conditions or when carrying heavy loads?
Right again! You guys are grasping these concepts well. Remember – Safety First – Stability is Key in Maritime Design!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the calculations involved in determining the relevant radius of gyration of a ship based on its metacentric height and rolling period. It highlights the significance of these parameters in understanding ship stability and dynamics.
Detailed
Detailed Summary
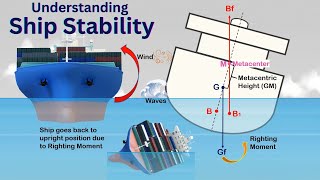
In this section, we discuss key principles of ship stability, focusing primarily on metacentric height (GM) and the period of rolling (T). A ship's stability is determined by its ability to return to an upright position after being tilted. The metacentric height is defined as the distance between the center of mass and the metacenter, which significantly influences the ship's behavior in water.
The main formula involved is related to harmonic motion concerning the ship's rolling motion represented mathematically as:
$$T = 2π\sqrt{GM/g}$$
Where:
- T is the period of rolling,
- GM is the metacentric height, and
- g is the acceleration due to gravity.
With a metacentric height of 0.3 meters and a rolling period of 20 seconds provided, the relevant radius of gyration can be determined, which is critical for assessing the stability and safety of the ship during uneven weather conditions or while navigating through turbulent waters. This exploration of metacentric height not only enhances our understanding of ship design but also offers valuable insights for practical applications in maritime engineering.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Ship Stability Concepts
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A ship has a metacentric height of 0.3 m and its period of rolling is 20 seconds.
Detailed Explanation
In ship design, the metacentric height (GM) and the period of rolling are critical for assessing stability. The metacentric height is the distance between the center of gravity of the ship and the metacenter, which is a point where the buoyant force acts when the ship is tilted. A higher metacentric height typically indicates better initial stability. The period of rolling (the time it takes to complete one full roll) gives insight into how quickly the ship responds to tilting. In this case, we see that the metacentric height is 0.3 meters and the rolling period is 20 seconds.
Examples & Analogies
Imagine a tall, thin tower versus a short, wide building. The tall tower (representing a ship with a high metacentric height) is more stable against strong winds initially, but if pushed too far, it can tumble over, similar to how a ship behaves. While the wide building (low metacentric height) may not roll over easily, it may sway longer and take time to return to its original position, akin to a ship with a longer rolling period.
Understanding the Metacentric Height and Rolling
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
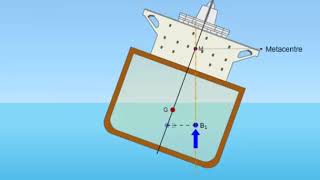
These are just sketched to say it the weight, the metacentric height and all the things. So the ship rotates about its longitudinal metacentric axis and it is considered as a pendulum.
Detailed Explanation
When a ship rolls, it pivots around its metacenter (the intersection of the vertical centerline and the center of buoyancy). By considering the ship as a pendulum, we can use the principles of harmonic motion to understand its behavior when tilted. As the ship rocks back and forth, it can be thought of as a pendulum, where the period of oscillation depends on the height at which it pivots (metacentric height) and the mass distribution (moment of inertia), which governs stability and responsiveness.
Examples & Analogies
Think of a child on a swing. The swing's height from which it hangs affects how fast it can sway back and forth. Similarly, a ship's metacentric height affects how quickly and smoothly it can return to an upright position after being tilted.
Restoring Moment and Oscillations
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If it is that, let me draw the free body diagrams. That means if it is the metacentric height here, this is the object is moving like this, okay? The oscillating is like a pendulum.
Detailed Explanation
The restoring moment is the force that brings the ship back to its upright position after it has been tilted. This moment depends on the ship's weight and how far it has tilted from its upright position. The moment of inertia also plays a critical role, as it quantifies how mass is distributed relative to the axis of rotation. When these forces are balanced, the ship will oscillate smoothly equivalent to a pendulum's motion.
Examples & Analogies
Imagine a seesaw with a child on one end. If the child leans too far to one side, the seesaw tilts, but the weight of the child on the other side causes it to return to balance. Similarly, a ship’s weight and metacentric height help it return to balance after being tilted.
Calculating Rolling Period and Radius of Gyration
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The time period is determined by the formula relating angular motion to restoring moments and moment of inertia.
Detailed Explanation
To find the radius of gyration (r) and how it relates to the ship's dynamics, we use the equation involving the period of rolling (T), which is connected to the metacentric height (GM) and moment of inertia (I). This equation helps to predict how fast the ship will roll back to upright when tilted. It links the gravitational force, the height from which the ship can restore itself, and the rotational inertia about its axis.
Examples & Analogies
Think about a gymnast performing on a balance beam. The gymnastic motion is similar to rolling, where the center of balance (metacenter) needs to be managed carefully. If their center of mass is too high or too low, it impacts how quickly they can regain balance after tilting.
Final Calculation and Results
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
20 = 2π√(GM/g) → GM = g * (20/(2π))².
Detailed Explanation
By substituting the values given for the rolling period and gravitational acceleration into the formula, we can calculate the metacentric height. This quantity provides insight into the stability characteristics of the ship. The resulting radius of gyration can then be computed based on the value obtained for GM, allowing us to understand how the mass distribution affects the ship's stability.
Examples & Analogies
Imagine you're designing a new bicycle. You’d consider how much weight is directly over the wheels (metacentric height) to ensure stability during turns. Similarly, knowing the radius of gyration helps determine how easily the bike can tip over when you lean to one side.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Metacentric Height: A critical parameter for assessing ship stability.
-
Rolling Period: The time period in which a ship rolls back to equilibrium.
-
Radius of Gyration: An essential factor in the calculation of ship stability.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A ship with a metacentric height of 0.3 m rolling period of 20 seconds can help determine the ship's stability during design phases.
-
Understanding how changes in metacentric height affect ship stability can prevent capsizing.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
To keep the ship steady, GM's your best friend, it helps her to ride, through each wave and bend.
📖 Fascinating Stories
-
Imagine a ship escaping from a storm, its GM high allows it to remain calm and steady.
🧠 Other Memory Gems
-
Remember GM = Great Maneuverability for stability at sea.
🎯 Super Acronyms
RGR - Remember GM, Good Rolling for ships.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Metacentric Height (GM)
Definition:
The distance between the center of gravity of a ship and its metacenter, impacting the ship's stability.
-
Term: Rolling Period (T)
Definition:
The time taken by a ship to complete one full roll back to equilibrium.
-
Term: Radius of Gyration (r)
Definition:
A measure of how far from the axis of rotation the mass of the ship is distributed.