Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Capillarity
Unlock Audio Lesson
Today, we will discuss capillarity, which is the ability of a liquid to flow in narrow spaces without the assistance of external forces. Can anyone tell me what causes this phenomenon?
Is it because of surface tension?
Exactly! Surface tension is a crucial factor. The upward force created by surface tension must equal the downward force due to gravity for the liquid to rise. This creates a balance.
So, how do we express this mathematically?
Great question! We can express it as T cos(θ) = ρgh, with T being the surface tension, θ the angle of contact, and ρg the weight of the liquid.
Remember the acronym CAP—Cohesion, Adhesion, and Pressure. It reminds us of the forces at play in capillarity.
Got it! So, cohesion attracts liquid molecules to each other, and adhesion pulls them towards solid surfaces.
Exactly! And this balance of forces leads to capillary rise in tubes. Let's summarize: capillarity stems from surface tension and is crucial for understanding fluid behavior.
Deriving Capillarity Relationships
Unlock Audio Lesson
Next, let's derive the relationships between capillary height and the angle of contact. What is the role of diameter here?
Does a smaller diameter lead to a higher capillary rise?
Yes! The smaller the diameter, the higher the rise due to increased surface area relative to volume. We derive this mathematically by relating the surface tension to weight.
Can you show us the mathematical relationship?
Absolutely. We have the formula h = (2T cos(θ)) / (ρg r), where 'r' is the radius. This shows that height 'h' depends directly on surface tension and inversely on density and radius.
A mnemonic to remember this is 'SHRINK' - Surface tension, Height, Radius, Inverse relationship, Numetric balance and Kinetics of fluids.
That makes it easier to remember! What happens at larger diameters?
At larger diameters, the effect lessens, demonstrating that the height of the liquid in larger tubes is significantly lower than in narrower tubes. This balance is critical in many engineering applications.
To summarize, we must understand how capillary height is inversely related to the diameter of the channel due to surface tensions.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section delves into the principles of capillarity in fluids, exploring the forces at play due to surface tension and how these impact the height of fluid rise against gravity. It focuses on the equilibrium of forces, deriving the relationships involving capillarity height, angle of contact, and diameters of annular systems.
Detailed
Capillarity Height and Angle of Contact
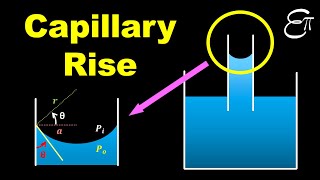
In fluid mechanics, the phenomena of capillarity arise from the interplay of cohesive and adhesive forces acting on a fluid at a surface. The upward force generated by surface tension counteracts the weight of the liquid column, leading to the rise of fluid in narrow tubes or porous materials.
Key equations describe this equilibrium:
- The upward force, stemming from surface tension (T), is determined by contributions from different radii of the contact area, while the downward force relates to the weight of the liquid column described by its height and the fluid's density.
- The balance between these forces leads to the derivation of essential relationships illustrating how the height of capillarity (h) is influenced by the angle of contact (θ) and the diameters of the liquid channels.
- The section highlights the significance of these phenomena in practical applications such as fluid transportation and engineering design, demonstrating that understanding these relationships is crucial for effective problem-solving in fluid dynamics.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Equilibrium of Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now I have just equating this since is a equilibrium conditions in the so upward force is equal to the downward force. Upward force = downward force.
Detailed Explanation
In this section, we explore the concept of equilibrium in fluid statics, particularly in capillarity. This idea states that in a static fluid, the upward force resulting from surface tension acting on the fluid at two different diameters must equal the downward force due to the fluid's weight. This balance of forces is crucial for understanding how liquids rise in narrow tubes or spaces due to capillary action.
Examples & Analogies
Imagine trying to lift a heavy object off a table with the help of a friend. If both of you pull up at the same time (like the upward forces), and the object weighs just right (like the downward force), it will move up smoothly. This balance of forces is analogous to how fluids behave in capillarity.
Surface Tension Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The upward force is a surface tension force part, that what will act for a two different diameters. That what will give you this component as the upward force.
Detailed Explanation
Surface tension arises due to the cohesive forces between liquid molecules, and it plays a crucial role in lifting liquids in confined spaces. In a capillary tube with different diameters, surface tension creates an upward force that counteracts the weight of the liquid column. This upward force can be computed based on the tension of the liquid and the dimensions of the tube.
Examples & Analogies
Consider how a small straw takes up a drink. If you place your finger on top, the liquid stays up thanks to surface tension. When the straw's diameter changes, like going from a large straw to a small one, you notice how much harder it can be to sip—this is similar to how surface tension varies with diameter.
Weight of the Fluid
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we can compute the downward force which is the weight of the fluid. That what we confined by this the capillary rise.
Detailed Explanation
The weight of the fluid in the capillary tube acts downward due to gravity and must be considered when analyzing the balance of forces. This weight can be calculated using the liquid's density and the height of the fluid column within the tube. Essentially, it equals the mass of the liquid multiplied by the acceleration due to gravity.
Examples & Analogies
Think of a stack of books. The weight of the books pushes down due to gravity, just like the fluid's weight in the capillary tube. If you add more books, the stack becomes heavier, representing increased downward force, similar to how more fluid increases the weight in a tube.
Deriving the Relationship
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
That is what will give us the weight which is the weight of the fluid acting downwards, the upper part. So if I just rearrange these terms the finally, I will get this ones. That is what very basic way I will get it the relations between the capillarity height angle of contact and these two are the diameter of annular systems where you will have a and sigma stands for surface tensions.
Detailed Explanation
By rearranging the terms used to calculate the upward and downward forces, we can derive a fundamental relationship that links capillary height, the angle of contact, surface tension, and the diameters of the tube. This relationship is essential for understanding how high a liquid will rise in a capillary tube based on these factors.
Examples & Analogies
Imagine you are building a water fountain. The height that the water shoots up is determined by the pressure and the size of the pipes used. Just like in our study of capillarity, you can predict how high the water will reach based on the conditions you've set, much like predicting the height of fluid rise in a tube.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Capillarity: A crucial phenomenon explaining how liquids rise in small tubes due to surface tension.
-
Surface Tension: The force that causes liquid surfaces to act like a stretched elastic membrane.
-
Angle of Contact: The angle at which a liquid meets a solid surface and influences how far it can rise.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When a thin straw is placed in water, the water rises above the straw's level due to capillarity.
-
A plant's roots absorb water from the soil through capillary action in the narrow spaces between soil particles.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In a tube so thin, water will climb high, surface tension is the force that takes it nigh.
📖 Fascinating Stories
-
Imagine a tiny man climbing a thin rope — that’s the liquid in a straw, with surface tension being the grip that helps him rise.
🧠 Other Memory Gems
-
SAM - Surface tension, Angle of contact, Medium (diameter) - remember the key influences in capillarity.
🎯 Super Acronyms
CAP - Cohesion, Adhesion, Pressure - the forces that govern capillarity.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Capillarity
Definition:
The ability of a liquid to flow in narrow spaces without external forces, due to surface tension.
-
Term: Surface Tension
Definition:
The tendency of liquid surfaces to shrink into the minimum surface area possible.
-
Term: Angle of Contact
Definition:
The angle formed between the liquid surface and the solid surface at the line of contact.