Fluid Mechanics Problem Solving
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Equilibrium Conditions in Fluids
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're going to learn about equilibrium conditions in fluid mechanics. Can anyone tell me what happens when we have upward forces equaling downward forces?

I believe it means the fluid is in a stable condition?

Exactly! When forces balance, the system remains in equilibrium. For instance, if the upward force from surface tension equals the downward gravitational force, the fluid will remain at rest.

So, what are the forces involved in that scenario?

Good question! The upward force due to surface tension can be represented as (T1 + T2) Cos(θ) while the downward force is the weight of the fluid. It’s key to set these forces equal to solve fluid problems.

What do T1 and T2 stand for?

T1 and T2 are the surface tension forces acting at different points of the fluid. Remember, T stands for tension!

To remember the balance of forces in fluids, think of 'FuDo' for 'Force Up equals Force Down.'

That's a helpful way to recall it!

Great! To summarize, equilibrium in fluids arises when the upward forces, like surface tension, balance the weight of the fluid acting downward.
Practical Applications of Fluid Mechanics
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let's look at a practical problem. How would we determine the pressure needed to equalize two fluids in different pipes connected to a manometer?

We would need to know the densities of the fluids involved!

Exactly! We’d calculate based on the pressures and the heights of the fluids. Given that, what is the mass density of oil if it’s 900 kg/m³?

That's fairly standard according to the fluid properties!

Correct! We also need to use the density of mercury, which is 13,550 kg/m³. Now let's move to calculating the pressure difference.

How do we apply Pascal's law here?

Good question! Pascal's law states that when pressure is applied at any point in a confined fluid, the pressure change is transmitted undiminished throughout the fluid. This means we can set up equations based on the heights and densities for our calculations!

So can we write a general formula for these situations?

Indeed! It will look like P_total = ρgh, balancing for both sides to find our unknown pressure.

In summary, applying principles like Pascal's law helps us tackle real-world problems in fluid mechanics.
Fluid Statics and Dynamic Stability
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Let’s shift gears to fluid statics. What can we say about a ship's metacentric height in relation to its stability?

The metacentric height indicates stability! A higher value typically means more stability.

Exactly right! If the ship has a metacentric height of 0.3 m and a rolling time of 20 seconds, we can calculate its radius of gyration using these parameters.

Can you remind us what the formula is for that?

Sure! It’s related by the moment of inertia and the metacentric height. Remember, the more connected these measurements, the more precise our stability concerns.

How does this affect the design of boats or ships?

Great application! Designers need to ensure the metacentric height is sufficient to prevent capsizing under dynamic forces.

In summary, fluid statics informs us about the stability of submerged objects like ships through specific measurements and formulas.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
In this section, we explore how to equate upward and downward forces in fluid mechanics problems, particularly how surface tension and fluid weight interact in various scenarios. We also look into practical examples and illustrative problems that facilitate better understanding.
Detailed
In fluid mechanics, solving problems often requires understanding equilibrium conditions, where the upward forces (like surface tension) balance the downward forces (such as the weight of the fluid). This section delves into the specifics of calculating these forces and demonstrates how to derive relationships between capillarity height, contact angle, and diameter in annular systems. Moreover, practical applications and problem-solving examples illustrate these concepts. The significance lies in gaining a deeper understanding of fluid behavior under various conditions, which is crucial for successful engineering design and analysis.
Youtube Videos









Audio Book
Dive deep into the subject with an immersive audiobook experience.
Equilibrium of Forces
Chapter 1 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
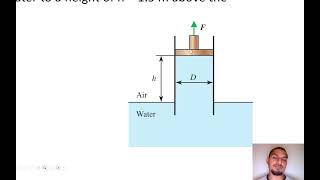
Now I have just equating this since is a equilibrium conditions in the so upward force is equal to the downward force.
Upward force = downward force (T1 + T2) Cos θ * h * (D² - d²)
T1 = σ × D
T2 = σ × d
Detailed Explanation
In fluid mechanics, when analyzing systems in equilibrium, we need to ensure that all the forces acting on the system are balanced. Here, the upward forces, which are created by surface tension in two different diameters (D and d), must equal the downward forces acting on the fluid due to its weight.
The formula includes terms for the upward force generated by surface tension, represented mathematically, where T1 is the tension at diameter D, T2 is the tension at diameter d, and σ represents the surface tension. By summing these forces using cosine of the angle θ and height h, we establish that the total upward force equals the weight of the fluid.
Examples & Analogies
Imagine a tightrope walker needing to keep their balance. Just as the walker's weight pulls them downward, the fluid's weight pulls down against the forces generated by surface tension which acts upward. If the forces are not equal, like a tightrope that's too slack, the system will fall out of balance.
Weight of the Fluid
Chapter 2 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
We can compute the downward force which is the weight of the fluid. That what we confined by this the capillary rise. That what will be σ (D + d) Cos θ = ρg * h * (σ × ρ / d²)
Detailed Explanation
Here, we calculate the downward force due to the weight of the fluid in the system. The weight is calculated by considering the volume of fluid affected by capillary action, which is related to the diameters D and d. This relationship can be expressed in terms of the gravitational force acting on this volume, where ρ is the fluid density and g is the acceleration due to gravity. The equation emphasizes how surface tension and fluid weight interact at equilibrium.
Examples & Analogies
This is similar to how a sponge absorbs water. The water held by the sponge has weight, which exerts downward pressure, while the surface tension helps hold water in place. If the sponge is too saturated, gravity overcomes the surface tension, and the water will drip out.
Capillirity Height Relation
Chapter 3 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This way, I get the relation between the capillarity height, angle of contact, and the diameters of the annular system, where σ stands for surface tensions.
Detailed Explanation
We derive a relationship that ties together the height a liquid will rise in a thin tube (capillary height), the angle at which the liquid contacts the tube (contact angle), and the diameters of the system. This demonstrates the fundamental principles of how fluids behave under the influence of cohesion (attraction between identical molecules) and adhesion (attraction between different substances). The capillarity height can be influenced by these factors, illustrating the unique behaviors of different fluids when they are in contact with solid surfaces.
Examples & Analogies
Think of how a paper towel absorbs spilled juice. The juice rises into the towel due to the interactions between the water molecules and the fibers of the towel, similar to the rise of water in a thin tube due to capillarity.
Encouragement on Understanding Fluid Mechanics
Chapter 4 of 4
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
In fluid mechanics, or any subject, we are encouraged to derive equations rather than memorize them. This enhances understanding and applying formulas correctly.
Detailed Explanation
Rather than just memorizing formulas, understanding their derivation and application is crucial in fluid mechanics. By doing this, students will not only be better prepared for exams but will also grasp how to apply these concepts in real-world situations. This approach fosters deeper comprehension and retention of knowledge.
Examples & Analogies
It's like learning to cook. Rather than memorizing recipes, if you understand the basic techniques (like how to sauté or bake), you can create a variety of dishes with what you have. Each recipe becomes easier to adapt and understand when you see the bigger picture.
Key Concepts
-
Equilibrium Conditions: Fluid forces must balance for stability.
-
Surface Tension: The force creates an upward lift in fluids.
-
Metacentric Height: An indicator of stability in floating bodies.
Examples & Applications
A fluid in a container remaining still while the forces acting on it are balanced.
Using pressure differences in a manometer to measure fluid flow rates.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In fluid mechanics, don't forget, forces balance, that's the safest bet!
Stories
Imagine a ship sailing smooth, its metacentric height ensures the groove. Without it, overboard it might move!
Memory Tools
Use H2O for 'Height equals height in Pressure Obligations!' for remembering fluid height vs pressure.
Acronyms
Use 'PRESS' for Pressure-Related Equations Simplifying Surface tension.
Flash Cards
Glossary
- Fluid Mechanics
The branch of physics that studies the behavior of fluids (liquids and gases) at rest and in motion.
- Surface Tension
The elastic tendency of a fluid surface that makes it acquire the least surface area possible, caused by intermolecular forces.
- Equilibrium
A state in which opposing forces or influences are balanced, often used in references to fluid forces.
- Manometer
An instrument that measures the pressure of a fluid by balancing it against a column of liquid.
- Metacentric Height
The distance between the center of buoyancy and the metacenter of a floating body, indicating its stability.
Reference links
Supplementary resources to enhance your learning experience.
