Dynamically Similar Conditions and Force Calculation
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Shear Stress and Viscosity
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we will delve into shear stress and viscosity. Does anyone know what shear stress is in a fluid?

Isn't it the force per unit area that acts parallel to the fluid's surface?

Exactly! And viscosity is the property that quantifies a fluid's resistance to shear. To help remember this, think of the acronym 'VISC' – Viscosity Indicates Shear Change.

So, higher viscosity means more resistance?

Correct! Can someone give me an example of a high-viscosity fluid?

Honey! It's very thick.

Great example! Let's summarize: shear stress is a force acting parallel to the surface, while viscosity is the fluid's resistance. Remember VISC!
Net Pressure Forces
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, moving onto net pressure forces. The net pressure force is crucial for understanding fluid flow. Can anyone express how we calculate it?

Is it the pressure difference over an area?

That's right! The equation is Net Pressure Force = Pressure Difference x Area. Let's make it memorable: 'Panel Area Pressure' – PAP.

And what about inertial forces? How do they fit in?

Excellent question! Inertial forces depend on mass and acceleration. They play a critical role in equations of motion for fluids.

Can we derive a relationship between pressure and inertial forces?

Exactly! By combining our knowledge of these forces through fluid mechanics' laws, we derive important ratios like Reynolds and Euler numbers.
Reynolds Number and Euler Number
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's discuss the Reynolds number. Who can tell me its significance?

It's the ratio of inertial to viscous forces!

Exactly! This helps us classify flow as laminar or turbulent. Can anyone remember how we calculate it?

Re = (Density x Velocity x Length) / Viscosity.

Perfect! Now, the Euler number relates pressure forces to inertia. To help remember, think of 'PEE' – Pressure to Energy Equivalence.

So both numbers help us analyze flow characteristics effectively?

Exactly! They guide engineers in practical applications like wind tunnel testing in automotive design.
Practical Application: Wind Tunnel Testing
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now, let's apply these concepts. How are dynamic similarities used in wind tunnel tests?

To model how cars behave in real airflow?

Exactly! By ensuring Reynolds numbers between models and prototypes match, we can predict drag forces accurately. What is one parameter we need to determine?

The drag coefficient, right?

Correct! This coefficient is essential in calculating the forces exerted on vehicles. Remember, 'Coefficient Counts' – C2.

What other parameters matter for the calculation?

Great question! Parameters like frontal area and velocity are also crucial in calculating aerodynamic drag.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section outlines the importance of dynamically similar conditions in fluid mechanics, explaining how shear stress, viscosity, and pressure forces are computed. It details the derivation of the Reynolds number and Euler number to compare inertial and viscous forces, demonstrating their application in real-world problems like automotive aerodynamics.
Detailed
Detailed Summary
In this section, we explore the concept of dynamically similar conditions essential for analyzing fluid behavior. The focus begins on shear stress and the calculations involving viscosity in fluid elements subjected to various stimuli. Key formulas related to shear forces are introduced, which help in calculating net pressure forces and inertia forces for steady flow scenarios.
The treatment of fluid dynamics involves deriving relationships between inertial and viscous forces, particularly emphasizing the significance of the Reynolds number as a ratio of these forces. As related concepts, Euler numbers also help understand flow characteristics in both model and prototype contexts.
Practical examples demonstrate these theories in action, such as testing cars in wind tunnels to assess aerodynamic drag, using known parameters like model width, frontal area, drag coefficients, and flow velocity. Similar analysis is applied to laminar flow over spheres, illustrating how dynamic similarity principles guide force calculations effectively.
Overall, the section serves as a bridge between theoretical fluid dynamics concepts and their practical applications, showcasing the foundational equations that continue to influence modern fluid mechanics.
Youtube Videos



![Buoyancy of Floating Objects [Physics of Fluid Mechanics #31]](https://img.youtube.com/vi/26Q1o6c5bjg/mqdefault.jpg)





Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Shear Stress and Viscosity
Chapter 1 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now just to look it, I am not going detail derivations of this part if you take a fluid element along a stimuli like this is the fluid element okay, this is the stream line which is having dx and dn dimensions, you have the shear stress which is changing at this along the n’th directions and you get it what could be the shear stress. Similar way you can find out the pressure values and all.
Detailed Explanation
In this part, we are discussing fluid elements and their behavior under stress. A fluid element is a small quantity of fluid that is analyzed to determine how it behaves under various forces. The shear stress within the fluid changes as it moves along certain directions due to the influences like friction and pressure. Visualizing this helps to understand how forces affect fluid flow and can assist in calculations for engineering applications.
Examples & Analogies
Imagine spreading butter on bread. The force you apply while spreading it causes the butter to change shape, similar to how shear stress works in fluids. The way the butter moves and spreads can help visualize how fluids respond to external forces.
Calculating Viscosity and Shear Force
Chapter 2 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Force due to the viscosity (friction) is ... The shear force can be expressed as ... Then you can compute the force due to the viscosity that will be the change of shear stress into the volumetric part. That is what if you portrait you get it this part.
Detailed Explanation
Viscosity is a measure of a fluid's resistance to flow. The shear force arising from viscosity can be calculated using specific equations, taking into account the dimensions and properties of the fluid. By understanding the relationship between shear stress and viscosity, we can calculate how those forces influence fluid flow.
Examples & Analogies
Think of honey flowing out of a jar versus water. Honey is more viscous, meaning it flows more slowly and requires more force to move. This scenario helps us understand how different fluids behave under stress based on their viscosity.
Net Pressure and Inertia Force
Chapter 3 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The net pressure force ... For steady flow, Inertia force computation ... Similar way the net pressure force acting of this you can see it will be this part and inertia force computation which is the, in case of the steady flow, mass into the acceleration or rate of change of the momentum flux that is what the mass and the momentum flux but you compute it, that along the stimuli directions will give us the inertia force components.
Detailed Explanation
The net pressure force acting on a fluid, combined with inertia forces, is crucial for understanding fluid dynamics in a system. The inertia force can be calculated using the mass of fluid multiplied by acceleration. This helps in analyzing how fluids behave when they are in motion or experiencing changes in velocity, vital for designing systems where fluid motion is involved.
Examples & Analogies
Consider a car accelerating on a road. The pressure from the ground (friction) allows it to move forward, while the mass of the car and how quickly it accelerates relate to inertia. This analogy illustrates how forces and inertia play a part in fluid behavior.
Dynamic Similarity in Fluid Mechanics
Chapter 4 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
If you equate it and substitute this values in case of loss of dynamic similarities ... Reynolds numbers.
Detailed Explanation
Dynamic similarity is vital in fluid mechanics as it ensures that the scaled models behave similarly to the real system under study. By analyzing the relationship between forces (inertia and viscous forces) through the Reynolds number, engineers can predict the flow behavior in both models and prototypes, thus simplifying experimental designs and increasing accuracy.
Examples & Analogies
Think of scaling a roller coaster model to test it in a water tank. Ensuring that the forces acting on both the model and the full-sized version behave dynamically similar allows the engineers to predict how safe and effective the ride will be without constructing the entire ride first.
Practical Application: Aerodynamics Testing
Chapter 5 of 5
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now let us come back to examples like this, let us have a testing of automobiles in a wind tunnel ... The data is what is given is model width frontal area, testing velocity, the scale, drag coefficient.
Detailed Explanation
To apply the theories of dynamic similarity to real-world problems, engineers often conduct experiments in controlled settings like wind tunnels. By gathering parameters such as car width, frontal area, velocity, and drag coefficient, engineers can compute the required power to overcome aerodynamic drag, allowing for efficient car design and optimization.
Examples & Analogies
When testing a new car prototype in a wind tunnel, the collected data helps designers make modifications before full-scale production, similar to trying on clothes at a store before buying them to ensure the best fit.
Key Concepts
-
Dynamic Similarity: The condition where two flows exhibit similar behavior under different scales.
-
Shear Stress: The stress component parallel to the fluid flow that influences motion.
-
Reynolds Number: A pivotal number used in fluid dynamics to predict flow patterns based on inertial and viscous forces.
Examples & Applications
In wind tunnel testing, one calculates the power required to overcome drag based on model data.
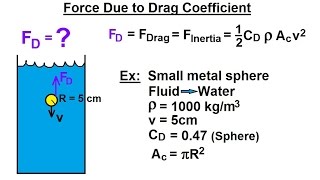
When analyzing a sphere in laminar flow, Reynolds numbers help determine drag forces.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
Shear stress on the surface lies, Viscosity thickens, that’s no surprise.
Stories
Imagine honey flowing slowly on a surface, illustrating how viscosity resists changes in motion.
Memory Tools
Remember R.E.V. for Reynolds Equivalent Viscosity in flows.
Acronyms
PAP for Net Pressure Force
Pressure Area Product.
Flash Cards
Glossary
- Shear Stress
The force per unit area acting parallel to a fluid's surface.
- Viscosity
The measure of a fluid's resistance to flow; higher viscosity indicates thicker fluids.
- Reynolds Number (Re)
A dimensionless number used to predict flow patterns in different fluid flow situations.
- Euler Number
A dimensionless number that relates pressure forces to inertial forces in fluid dynamics.
- Drag Coefficient
A dimensionless number that quantifies the drag or resistance of an object in a fluid environment.
Reference links
Supplementary resources to enhance your learning experience.
