Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Shear Stress
Unlock Audio Lesson
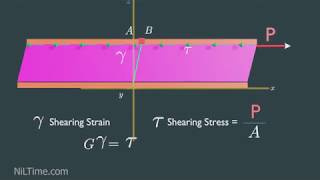
Let's start our discussion with shear stress in fluids. Shear stress is the force per unit area exerted parallel to a surface. It plays a critical role in fluid motion. Can anyone explain how this affects the flow of fluids?
So, if the shear stress is high, does that mean the fluid flows faster?
Exactly! High shear stress indicates a strong force that can lead to faster movement. Now, who can tell me how shear stress is calculated?
Is it related to viscosity and the shear rate?
Yes! We can express shear stress using the equation τ = μ * (du/dy), where τ is the shear stress, μ is the viscosity, and du/dy is the shear rate. A helpful memory aid is 'Viscous Yo-Yo' – think of how the more you stretch a yo-yo, the more it tries to resist!
How does viscosity impact real-world applications?
Great question! Viscosity affects everything from blood flow in arteries to oil transport in pipelines. Instead of just being a term, it influences many engineering designs!
To summarize, shear stress is pivotal in fluid movement, calculated in relation to viscosity and shear rate.
Net Pressure and Inertia Forces
Unlock Audio Lesson
Moving on, let’s talk about net pressure forces acting on a fluid. These forces contribute to how fluids flow through systems. Can someone explain what factors might influence these forces?
I think the cross-sectional area and fluid density matter?
Precisely! The net pressure force is calculated using the equation F = P * A, where P is pressure and A is the area. Another critical aspect is inertia, which is basically the fluid's resistance to changes in its motion.
So, how do we calculate inertia forces?
Good question! Inertia force can be calculated as F = m * a. Here, mass is the density of the fluid multiplied by volume, and acceleration comes from changes in velocity over time.
What’s this Reynolds number they mentioned back in the text?
Ah, the Reynolds number is a dimensionless number that helps determine flow regimes. It’s the ratio of inertia forces to viscous forces, which we can find using Re = (ρ * V * L) / μ. A mnemonic to remember this is 'Rats Vent Luxury' where each word starts with R, V, and L for Reynolds number, velocity, and length scale.
In summary, we thoroughly discussed net pressure forces and how inertia plays a role in fluid dynamics, focusing on their calculations.
Applying Knowledge Through Example Problems
Unlock Audio Lesson
Now that we understand the basics, let's dive into some example problems. Can someone describe how we can calculate drag force on a vehicle in motion?
We need to know the drag coefficient, the frontal area, and the fluid density right?
Correct! The drag force can be calculated using F_d = C_d * (ρ * V² * A) / 2. What does each variable represent?
C_d is the drag coefficient, ρ is the fluid density, V is the velocity of the fluid and A is the frontal area.
Exactly! For example, consider you have a vehicle with a frontal area of 7.8 m² moving at a velocity of 100 km/h with a drag coefficient of 0.46. What would be the drag force?
Let me convert that to m/s... It’s about 27.78 m/s. Then, using the drag force equation, we can calculate it.
After plugging in the values, the answer we get is around 1697 N.
Well done! Not only did you calculate the drag force, but you also showcased how the principles change in real-world applications. To summarize, applying theoretical knowledge through practical examples cements our understanding.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses shear stress and its applications, as well as the effects of viscosity and the net pressure force on fluid flow. Important parameters such as Reynolds and Euler numbers are introduced, along with practical applications in aerodynamics and fluid testing.
Detailed
Forces and Shear Stress in Fluids
In fluid mechanics, the study of shear stress and viscosity is crucial in understanding the behavior of fluids under various conditions. Shear stress in a fluid is defined as the force per unit area acting parallel to the fluid's motion, and it can vary along different coordinates within the fluid stream. Viscosity, a key parameter representing internal friction in fluids, influences how shear stress affects flow behavior.
Key Concepts:
- Shear Force: Expressed as a product of viscosity and shear rate, representing forces acting on fluid elements.
- Net Pressure Force: The total pressure acting on a fluid element, which affects flow characteristics and dynamics.
- Inertia Forces: Important in steady flow analysis, calculated as mass multiplied by an acceleration term.
- Reynolds Number: A dimensionless quantity that quantifies the ratio of inertia force to viscous force, providing insights into flow regimes (laminar vs. turbulent).
- Euler Number: Another dimensionless parameter that relates inertia and pressure forces.
The section further illustrates these principles through exercises and examples, such as aerodynamic drag in automotive applications and flow over a sphere. Understanding these concepts not only aids in mechanical and civil engineering design tasks but also has broader applications in economic modeling through fluid dynamics principles.
Youtube Videos
![Normal Stress And Shear Stress [Fluid Mechanics]](https://img.youtube.com/vi/3i2WeDFZ0fI/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Shear Stress in Fluids
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now just to look it, I am not going detail derivations of this part if you take a fluid element along a stimuli like this is the fluid element okay, this is the stream line which is having dx and dn dimensions, you have the shear stress which is changing at this along the n’th directions and you get it what could be the shear stress. Similar way you can find out the pressure values and all.
Detailed Explanation
In fluid mechanics, shear stress refers to the stress that acts parallel to the surface of a material. Considering a fluid element in a flow, we can visualize it as a small volume where the forces acting on it are derived from the surrounding fluid. As the fluid moves, the force acting at different points can change, generating shear stress. This is particularly important in the analysis of fluid flow along streamlines, where we can express the dimensions (dx and dn) to help understand these variations.
Examples & Analogies
Imagine a deck of cards. If you press down on one side and slide it slightly, the cards move relative to each other due to the forces applied. This sliding motion represents shear stress in fluids, where the layers of fluid slide over one another as they flow.
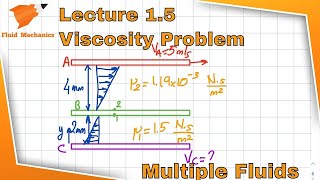
Calculating Viscous Forces
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Force due to the viscosity (friction) is expressed as shear force can be expressed as. Then you can compute the force due to the viscosity that will be the change of shear stress into the volumetric part.
Detailed Explanation
Viscosity is a measure of a fluid's resistance to deformation and flow. The force due to viscosity can be quantified by considering the shear stress acting on a fluid element and how it varies with changes in volume. The relation between shear stress and shear force can be expressed through equations that factor in the dimensions of the fluid element, allowing us to compute how much force is generated by the fluid's viscosity under different conditions.
Examples & Analogies
Think of honey being poured onto a plate. The thickness (viscosity) of the honey makes it flow slowly compared to water. If we measure the thickness as force acting through a certain area over time, we could compute the viscous forces and relate them to how quickly the honey spreads out.
Net Pressure Force in Steady Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The net pressure force for steady flow, inertia force computation.
Detailed Explanation
In a steady fluid flow, the net pressure force can be calculated by considering the balance of inertial forces and pressure forces acting on the fluid element. The inertia force is directly related to the mass of the fluid and its acceleration, leading to an expression that balances these forces. This equilibrium helps in analyzing different scenarios of fluid flow, especially in engineering applications.
Examples & Analogies
Imagine riding a bicycle on a smooth, straight road versus a hilly terrain. In a steady flow (like the smooth road), your body (the fluid element) feels consistent forces from the pedals (pressure forces) and encounters fewer abrupt changes, allowing for easier calculation of required effort (net pressure force). In contrast, on hilly terrain, the variations in incline (inertia forces) change how you pedal, complicating the computation.
Dynamic Similarity and Reynolds Number
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you equate it and substitute these values in case of loss of dynamic similarities the ratio between these part, you can see that these equations comes out to be the Reynolds and this equations comes out to be the Euler strength.
Detailed Explanation
Dynamic similarity refers to the comparison of fluid flow patterns under different conditions. It allows us to relate smaller model experiments to full-scale conditions using dimensionless numbers such as Reynolds number and Euler number. Reynolds number, which compares inertial forces to viscous forces, is particularly important in predicting flow behaviors, while Euler number relates pressure forces to inertial forces, broadening our understanding of fluid dynamics.
Examples & Analogies
Consider testing a small toy car in a water stream to understand how a full-sized car behaves in real conditions. By analyzing the toy car's flows, you can deduce how the larger car would respond under similar conditions, calculated using parameters like the Reynolds number to ensure that the forces acting are proportionally similar.
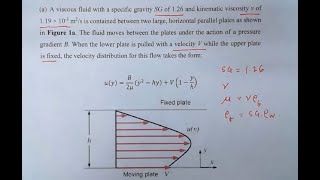
Practical Applications and Problem-Solving
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come back to examples like this, let us have a testing of automobiles in a wind tunnel to find the aerodynamic drags, the power required to overcome this drag part...
Detailed Explanation
This chunk highlights the practical application of fluid mechanics principles in real-world engineering problems. By conducting tests in controlled environments like wind tunnels, we can measure forces acting on vehicles, which helps in design and efficiency improvements. The calculations involve determining drag forces based on parameters like vehicle shape, speed, and air density, and relate back to the theories discussed earlier, integrating concept with application.
Examples & Analogies
Thinking about how a bird flies can be insightful. Just like engineers use wind tunnels to gauge how shape affects flight (drag force), birds naturally adjust their wings to prevail against air resistance, showcasing the fundamental principles of fluid dynamics in nature.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Shear Force: Expressed as a product of viscosity and shear rate, representing forces acting on fluid elements.
-
Net Pressure Force: The total pressure acting on a fluid element, which affects flow characteristics and dynamics.
-
Inertia Forces: Important in steady flow analysis, calculated as mass multiplied by an acceleration term.
-
Reynolds Number: A dimensionless quantity that quantifies the ratio of inertia force to viscous force, providing insights into flow regimes (laminar vs. turbulent).
-
Euler Number: Another dimensionless parameter that relates inertia and pressure forces.
-
The section further illustrates these principles through exercises and examples, such as aerodynamic drag in automotive applications and flow over a sphere. Understanding these concepts not only aids in mechanical and civil engineering design tasks but also has broader applications in economic modeling through fluid dynamics principles.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Calculating shear stress in a fluid flowing over a surface.
-
Determining drag force on a car in a wind tunnel test.
-
Comparing Reynolds numbers for different flow conditions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Shear means slide, stress will abide, as forces combine, fluid paths decide.
📖 Fascinating Stories
-
Imagine a river flowing swiftly past a rock. The water creates different shear stresses on the upstream and downstream sides. This helps visualize how fluids interact under shear forces.
🧠 Other Memory Gems
-
Rats Can Always Make It (Reynolds, Coefficient, Area, Mass, Inertia) to remember the relations in Fluid Dynamics.
🎯 Super Acronyms
VIP (Viscosity, Inertia, Pressure) helps remember these fundamental concepts in fluid mechanics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Shear Stress
Definition:
Forces per unit area acting in parallel to the fluid flow.
-
Term: Viscosity
Definition:
A measure of a fluid's internal resistance to flow.
-
Term: Reynolds Number
Definition:
A dimensionless number representing the ratio of inertial forces to viscous forces in a fluid.
-
Term: Net Pressure Force
Definition:
The total force exerted by pressure acting on a fluid element.
-
Term: Inertia Force
Definition:
The force that describes the resistance of a fluid to changes in motion.
-
Term: Euler Number
Definition:
A dimensionless number representing the ratio of inertial forces to pressure forces in a fluid flow.
-
Term: Drag Force
Definition:
The resisting force experienced by an object in a fluid flow.
-
Term: Dynamic Similarity
Definition:
A condition where the flow characteristics of a model and its prototype are equivalent.