Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Wind Tunnel Testing
Unlock Audio Lesson
Today, we’re discussing how automobiles are tested in wind tunnels to determine aerodynamic drag. Can anyone tell me why drag is significant in automobile design?
It affects the fuel efficiency of the vehicle!
And it influences the top speed, too!
Exactly! Reducing drag is crucial for better fuel efficiency and performance. Can anyone remind us what we mean by aerodynamic drag?
It's the resistance experienced by an object moving through air.
Great! Now, let’s talk about how we measure this drag in a wind tunnel.
Key Forces in Fluid Dynamics
Unlock Audio Lesson
To analyze drag, we consider various forces acting on an automobile. What can we say about viscosity?
Viscosity is how resistant a fluid is to flow.
Correct! Viscosity affects shear stress in the fluid. What do we use to quantify the relationship between inertia and viscous forces in a flow?
The Reynolds number!
Exactly! The Reynolds number tells us whether the flow is laminar or turbulent. Can anyone remind me how it’s calculated?
Calculating Power Required to Overcome Drag
Unlock Audio Lesson
Now, let's calculate the power required to overcome drag in an automobile model. If we have a frontal area and drag coefficient, how would you calculate the drag force?
We can use the equation: Drag force = Drag coefficient * Density * Velocity^2 * Area.
That's right! After calculating drag, we can also find the power needed using the formula Power = Drag force * Velocity. Can someone provide the power in kilowatts if drag force is 1697 N?
It would be about 47.139 kW!
Excellent! Remember, higher power is typically needed for larger vehicles or at higher speeds.
Dynamic Similarity in Modeling
Unlock Audio Lesson
We've established the drag force. Now, why is it important to ensure dynamic similarity between the model and the prototype during testing?
To make sure the results we get can be scaled up to real-world conditions!
Exactly! If they are dynamically similar, we can accurately predict how the prototype will behave. This ties back to our calculations and the Reynolds number, doesn’t it?
Yes! The Reynolds number for both the model and the prototype needs to match.
Correct! That ensures that the flow conditions are similar, leading to valid experimental results.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section covers the principles of testing automobiles in wind tunnels, focusing on calculating dynamic forces such as pressure and shear due to viscosity. It presents key formulas to compute the power required to overcome drag, taking into account parameters like frontal area, velocity, and drag coefficient.
Detailed
Testing of Automobiles in Wind Tunnel
In this section, we explore the process of testing automobiles in a wind tunnel to determine aerodynamic drag force and the corresponding power required to overcome this drag. The focus is on understanding the relationships between pressure, shear stress, and velocity, employing key principles of fluid dynamics such as the Reynolds number and Euler number.
The discussion starts with the basics of shear stress and pressure values related to fluid elements, emphasizing the influence of viscosity and Cavalieri's principle in dynamics. We compute the net pressure force in steady flow conditions, integrating Newton's laws of viscosity.
Key Concepts:
- Forces due to Viscosity: The computed shear force and pressure force are analyzed in the context of viscous and inertial forces, leading to the derivation of the Reynolds number, which plays a critical role in dynamic similarity conditions for models and prototypes.
- Model Testing: The practical example involves an automobile model scaled at 16:1, detailing parameters such as model width, frontal area, and drag coefficient, while deriving the power needed at the prototype level from standard fluid flow equations.
By plugging in data such as air density and testing velocity, we arrive at necessary calculations for dynamic viscosity, Reynolds numbers, and ultimately the drag force and required power to counteract this drag.
Through real examples, including flow over a sphere, we illustrate these fluid dynamics concepts in a way that prepares students for practical applications of fluid mechanics, furthering their understanding and curiosity about its relevance to various fields, including urban economics.
Youtube Videos
![[Fluid Dynamics: Physical Modelling] Reynolds Similitude, P2: wind tunnel tests and examples (2/2)](https://img.youtube.com/vi/-9NvoAIhMq0/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Wind Tunnel Testing
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now let us come back to examples like this, let us have a testing of automobiles in a wind tunnel to find the aerodynamic drags, the power required to overcome this drag part. The data is what is given is model width frontal area, testing velocity, the scale, drag coefficient.
Detailed Explanation
Wind tunnel testing is a method used to study the aerodynamic performance of vehicles, such as automobiles. In this process, the vehicle model is placed in a controlled environment where air is blown over it at various speeds. The key parameters we measure include the aerodynamic drag, which is the resistance faced due to air when the vehicle is in motion, and the power needed to overcome that resistance. To conduct this test, certain data inputs are required, including the model dimensions, the frontal area that faces the airflow, the testing velocity, the scale of the model compared to the actual car, and the drag coefficient, which quantifies the drag force acting on the vehicle.
Examples & Analogies
Think of wind tunnel testing like testing how a person rides a bicycle in a windstorm. Just as the biker faces resistance from the wind, cars face drag when they move. By measuring how much force is needed to pedal against the wind, we can understand how design changes affect performance, such as how a more streamlined helmet reduces wind resistance.
Given Data for Testing
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Given Data
Model width : 2.44 m
Frontal Area : 7.8 m²
Testing Velocity : 100 km/h
Scale : 16:1
Drag Coefficient : 0.46
To determine the power required for prototype Parameters
At standard sea level: p=101325 Pa, T=288 K
p
ρ = 1.226 kg/m³
RT
μ = 1.46 x 10⁻⁵ kg/m·s
T
= 111
μ = 1.79 x 10⁻³ kg/m·s
Detailed Explanation
For the testing to be valid, it is crucial to define certain parameters. The model width of 2.44 m and frontal area of 7.8 m² defines the size and shape of our testing model. The testing velocity of 100 km/h specifies how fast the air must flow over the model in the wind tunnel. A scale of 16:1 indicates that the model is 16 times smaller than the actual vehicle, allowing us to simulate its performance in a manageable size. The drag coefficient of 0.46 reflects the efficiency of the vehicle's design in terms of airflow. Additionally, the environmental conditions at the testing site – such as pressure and temperature – are provided to help calculate air density and viscosity, which are vital in computing the aerodynamic forces acting on the model.
Examples & Analogies
Using a model airplane in a wind tunnel gives a good analogy. The size of the model (scale) helps determine how accurately it will represent the real airplane in terms of performance. Just as the conditions like temperature and air pressure affect how the wings of the model behave, they similarly affect how much drag a car experiences when tested.
Calculating the Power Required
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Drag for the prototype:
D = C ρV² A
= 1697 N
Power to overcome this Drag = D V
= 1697 * (100 / 3.6)
= 47139 W
= 47.139 kW
Detailed Explanation
To find out how much power a prototype vehicle requires to overcome aerodynamic drag, we use the drag equation, which states that drag force (D) is equal to the drag coefficient (C) multiplied by the air density (ρ), the square of the velocity (V²), and the frontal area (A). Using the parameters, we calculate that the drag force is 1697 N. To find out how much power is needed, we multiply the drag force by the velocity (converted from km/h to m/s). The result is a power output of 47.139 kW, which gives us an idea of the engine power required to maintain speed against drag.
Examples & Analogies
Consider riding a bicycle against the wind. If you know how hard you have to pedal (the drag force) to maintain a certain speed, you can estimate the power output required to keep moving forward. Similarly, the calculations here show how engineers estimate how much energy a car engine must produce to drive efficiently under real-world conditions.
Dynamic Similarity and Reynolds Number
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
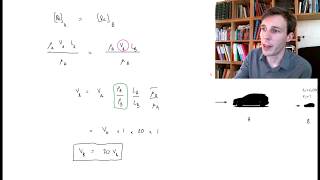
We use the dynamic similarities means the Reynolds numbers of the models should equal to the Reynolds numbers of the prototypes since the density and the μ.
Detailed Explanation
Dynamic similarity is a concept that helps ensure that the behavior of a model can accurately represent that of the full-scale prototype. One way to achieve dynamic similarity is by ensuring that the Reynolds number for both the model and the prototype is the same. The Reynolds number is a dimensionless quantity that helps predict flow patterns in different fluid flow situations. If the model's Reynolds number closely matches that of the full-scale vehicle, it suggests that the airflow behavior remains consistent, enabling predictions about aerodynamic performance.
Examples & Analogies
Imagine a swimming race where small children and professional swimmers are racing in separate pools. For the children, we could add obstacles to their pool to match the currents and waves in the professional swimmers' pool. By ensuring the swimming conditions for both groups are similar, we could better predict how well each group would perform in a real race, similar to matching Reynolds numbers for the test models and prototypes.
Conclusion on Aerodynamic Testing
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So just trying to show it if you look at the history of the pipe flow experiment... more discussion of these in the next class. Let me thank you for this lecture today.
Detailed Explanation
The conclusion wraps up the discussion on aerodynamic testing in wind tunnels and emphasizes the evolution of parameters and equations in fluid mechanics over the years. This history is critical as it informs modern practices and methodologies used today for both research and industry applications. Understanding these principles enables better vehicle design and performance insights.
Examples & Analogies
Much like how innovating in technology has roots in historical inventions, understanding fluid mechanics comes from building on past knowledge. Just as modern smartphone technology is layered upon decades of advancements in communication and computing, automobile testing techniques have developed from early discoveries in fluid dynamics.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Forces due to Viscosity: The computed shear force and pressure force are analyzed in the context of viscous and inertial forces, leading to the derivation of the Reynolds number, which plays a critical role in dynamic similarity conditions for models and prototypes.
-
Model Testing: The practical example involves an automobile model scaled at 16:1, detailing parameters such as model width, frontal area, and drag coefficient, while deriving the power needed at the prototype level from standard fluid flow equations.
-
By plugging in data such as air density and testing velocity, we arrive at necessary calculations for dynamic viscosity, Reynolds numbers, and ultimately the drag force and required power to counteract this drag.
-
Through real examples, including flow over a sphere, we illustrate these fluid dynamics concepts in a way that prepares students for practical applications of fluid mechanics, furthering their understanding and curiosity about its relevance to various fields, including urban economics.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An automobile in a wind tunnel exhibits different drag forces based on its shape and size.
-
Under specific conditions, the drag force on the scaled model can predict the full-sized prototype's behavior.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Drag can slow, it makes cars low, through wind the pressure will flow.
📖 Fascinating Stories
-
Imagine a car racing against the wind; the faster it goes, the harder the wind pushes back. The driver must know how to navigate this drag to win.
🧠 Other Memory Gems
-
D-Pv = Drag, Pressure, Velocity: Remember the forces acting on an auto in a wind tunnel.
🎯 Super Acronyms
DREAM = Drag Reduction Encouragement Using Aerodynamic Mechanics.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Aerodynamic Drag
Definition:
The resistance experienced by an object moving through air, affecting fuel efficiency and speed.
-
Term: Viscosity
Definition:
A measure of a fluid's resistance to flow and deformation.
-
Term: Reynolds Number
Definition:
A dimensionless quantity used to predict flow patterns in different fluid flow situations.
-
Term: Dynamic Similarity
Definition:
The condition where both model and prototype exhibit similar flow characteristics during testing.
-
Term: Power
Definition:
The rate at which work is done or energy is transferred, commonly required to overcome drag in vehicles.