Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Cylindrical Coordinates
Unlock Audio Lesson
Today we will explore cylindrical coordinates and how they are applied in fluid mechanics. Can anyone tell me what cylindrical coordinates are?
Are they the coordinates that use a radius, angle, and height instead of just x, y, and z?
Exactly! In cylindrical coordinates, we use (r, θ, z), where 'r' is the radius from the axis of rotation, 'θ' is the angle around the axis, and 'z' is the height. Can anyone tell me why we might prefer cylindrical coordinates over Cartesian coordinates?
I think it's because they can simplify problems with circular symmetry.
Great point! This simplification helps when we solve problems that involve cylindrical shapes, like pipes or tanks.
Mass Conservation Equation Derivation
Unlock Audio Lesson
Now let's derive the mass conservation equations specific to cylindrical coordinates. To start, what is the general form of the mass conservation equation?
Is it... the rate of change of mass in a control volume equals the mass flux in and out?
Correct! When we derive it in cylindrical coordinates, we express the velocity field with components u_r, u_θ, and u_z. Who can summarize how the mass flux is handled in these components?
We would calculate the mass flux across the surfaces of our control volume, accounting for each directional component.
Exactly! By integrating these across the surfaces, we arrive at the specific forms of the continuity equations. Always remember, we can simplify using the Taylor series for small control volumes.
Applications of Cylindrical Coordinates
Unlock Audio Lesson
Let's discuss some practical applications of cylindrical coordinates. Can anyone think of a scenario in engineering where they would be useful?
Maybe in analyzing flow in pipes or round tanks?
Absolutely right! For example, in an internal combustion engine, we often model how fuel and air mixture flows in a cylindrical chamber. This lets us determine density changes during compression.
So, using cylindrical coordinates helps us more accurately predict how fluids behave in those situations?
Exactly! It allows us to capture the characteristics of the flow much better. That's the power of coordinate transformation!
Understanding Compressible vs Incompressible Flow
Unlock Audio Lesson
To wrap up, let’s differentiate between compressible and incompressible flows. Who can explain what we mean by incompressible flow?
I think it means the fluid density doesn't change, right?
Exactly! In compressible flow, density changes occur due to various factors like pressure and temperature changes. Can anyone give an example of a situation where we expect compressible flow?
How about the flow of gases at high speeds, like in aircraft?
Correct again! Understanding these differences is critical in fluid dynamics, especially when applying the mass conservation equations.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, the principles of mass conservation are explored within the context of cylindrical coordinate systems. The section provides a detailed derivation of the continuity equations, highlighting the application of these principles in solving fluid mechanics problems. Particular attention is given to how cylindrical coordinates simplify certain problems by better accommodating symmetry in flow situations.
Detailed
Detailed Summary of Cylindrical Coordinate Systems
This section focuses on the application of cylindrical coordinates to mass conservation equations, which are central in fluid mechanics. The mass conservation equations can be expressed through continuity equations, which serve as governing equations for fluid flow. In cylindrical coordinates, the velocity fields are expressed in terms of radial (u_r), angular (u_θ), and vertical (u_z) components.
The reader is guided through the derivation of mass conservation equations from fundamental principles, utilizing the concept of infinitesimally small control volumes. The dynamics of fluid flow are observed as mass flux is established in terms of density (ρ) and velocity (v), leading to equations that describe the rate of change of mass storage within the control volume.
The section also elaborates on the Gauss theorem's application in deriving these equations, smoothly transitioning into defining the differences when working in cylindrical versus Cartesian coordinate systems. It concludes with a discussion on the physical interpretations of compressible and incompressible flow, with examples illustrating the practical application of these concepts, particularly in the context of internal combustion engines.
Youtube Videos
![Navier-Stokes in cylindrical coordinates [Fluid Mechanics #9a]](https://img.youtube.com/vi/mkb9y8N2y_Q/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Cylindrical Coordinate Systems
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Many of the problems we can use a cylindrical coordinates to solve it because it will be easier for imposing the boundary conditions also we can solve the problems.
Detailed Explanation
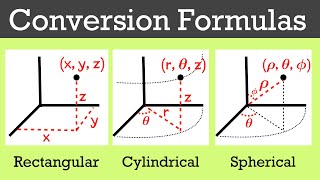
Cylindrical coordinate systems are commonly used in fluid mechanics, particularly when dealing with problems that have some symmetry about a central axis. In these systems, instead of using Cartesian coordinates (x, y, z), we use cylindrical coordinates (r, θ, z). The radial distance (r) represents the distance from the axis of rotation, θ represents the angular position around the axis, and z represents the height along the axis. This makes it easier to set up boundary conditions and equations for certain types of problems, especially ones that involve circular motion or are cylindrical in nature.
Examples & Analogies
Imagine you have a can of soda. The surface of the can is curved, and if you wanted to describe a point on its surface, using cylindrical coordinates (which account for the curves and circular symmetry) would make it simpler than trying to pinpoint it using straight x and y coordinates.
Geometric Relationships in Cylindrical Coordinates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
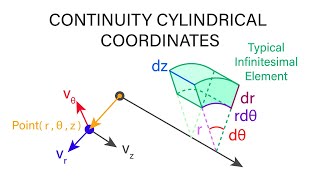
That means earlier we have considered a parallel piped control volumes instead of taking the parallel pipe control volumes we are considering a control volumes which is having a radial d dimensions of dr d theta and perpendicular to this will be the dr d theta and perpendicular will be the dz.
Detailed Explanation
In cylindrical coordinates, the control volumes used for analyzing fluid flow are not rectangular prisms as in Cartesian coordinates, but instead are shaped like cylindrical slices. These slices have a radial thickness (dr), an angular width (dθ), and a vertical height (dz). This format accounts for the curvature of the fluid flow and reflects the true geometry of many engineering systems involving pipes or rotational bodies. Thus, the equations derived will be based on these dimensions, maintaining accuracy for real-world applications.
Examples & Analogies
Consider analyzing the flow of water inside a large circular pipe. Using cylindrical coordinates will help describe the flow much better than Cartesian coordinates because Water flows along the curves of the pipe naturally, and using cylindrical coordinates allows you to capture this behavior with ease, similar to how a map of the Earth is typically done in a spherical format rather than as a flat rectangle.
Transformation from Cartesian to Cylindrical Coordinates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
we are looking converting to the cylinder coordinate systems having the relationship with R 10 theta and the XY. that is what is the relationship here that is what is a simple the graphically if you look at that x will be the r cos theta, y will be r sin theta and theta will be the tan theta equal to y by x.
Detailed Explanation
To convert from Cartesian coordinates to cylindrical coordinates, we use specific mathematical relationships. In cylindrical coordinates, the x and y coordinates are expressed as x = r cos(θ) and y = r sin(θ). Here, 'r' is the distance from the origin to the point of interest, and 'θ' is the angle in relation to the positive x-axis. This transformation is crucial for simplifying calculations where circular or cylindrical symmetry exists, making it easier to analyze fluid flow and other physical phenomena.
Examples & Analogies
Think of a Ferris wheel at an amusement park. To locate a seat, you can describe its height above the ground and how far it is from the center of the Ferris wheel (using cylindrical coordinates). You would say it's 10 feet high (z) and 4 feet from the center (r) at a certain angle θ from the starting point. Using this cylindrical system makes it simpler to find your seat compared to trying to calculate its exact position using a flat x-y grid.
Mass Conservation in Cylindrical Coordinates
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
If you look at this cylindrical coordinate systems we define the velocity field as ur is a radial velocity component u theta this is the velocity components in the angular directions you can look it okay this is radial point angular point and you have the perpendicular to that is the uz representing r theta and z.
Detailed Explanation
In cylindrical coordinates, the velocity field is expressed in terms of three components: ur (the radial velocity), uθ (the angular velocity), and uz (the vertical velocity). These components help describe how fluid flows in three-dimensional space where cylindrical symmetry is present. This distinction is important in fluid dynamics because it allows for more accurate predictions concerning fluid behavior based on its orientation and the forces acting on it. When applying mass conservation principles, these velocity components are used to describe how mass enters, exits, or resides within a given volume.
Examples & Analogies
Imagine a garden hose connected to a rotating sprinkler head. The water shoots out radially (ur) while the sprinkler also spins around (uθ). If you wanted to calculate how much water moves through the sprinkler per minute, you'd use both radial and angular velocities. This scenario illustrates how both components are necessary for describing the complex flow patterns in situations involving circular motions.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Cylindrical Coordinates: A system defined by radius, angle, and height.
-
Mass Conservation: The principle that mass cannot be created or destroyed in a closed system.
-
Continuity Equation: Relates the density and velocity of the fluid within a control volume.
-
Compressible Flow: Flow characterized by density changes.
-
Incompressible Flow: Flow where density remains constant throughout.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Cylindrical coordinates are often used to analyze fluid flow within pipes or round tanks, where symmetry simplifies the problem.
-
The mass conservation equation can be applied to predict how the density of a fluid changes during compression in an internal combustion engine.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In cylindrical flow, r and θ do glow, z is height, all in tow.
📖 Fascinating Stories
-
Imagine a chef pouring soup into a cylindrical pot. As the pot fills, the soup's density changes as more ingredients are added, illustrating how mass conservation works.
🧠 Other Memory Gems
-
Remember the 'C-C' (Cylindrical Coordinates) for circular problems - they just fit like gloves!
🎯 Super Acronyms
Remember 'M-F-I'
- Mass is conserved
- Fluid is analyzed
- In a control volume.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Cylindrical Coordinates
Definition:
A three-dimensional coordinate system that uses a radial distance, an angle, and height to specify points.
-
Term: Mass Conservation Equation
Definition:
A principle stating that the mass within a control volume cannot change if there are no mass sources or sinks.
-
Term: Incompressible Flow
Definition:
A flow regime where the fluid density remains constant.
-
Term: Compressible Flow
Definition:
A flow regime in which the fluid density varies due to pressure or temperature changes.
-
Term: Velocity Field
Definition:
A vector function that describes the velocity of fluid flow at different points in space.