Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Fluid Flow Types
Unlock Audio Lesson
Today, we are going to explore the concepts of incompressible and compressible flow. Firstly, can anyone tell me what distinguishes these two types of fluid flow?
In incompressible flow, the density remains constant, right?
Exactly! And what about compressible flow?
In compressible flow, the density changes with pressure or temperature?
Great! Now, remember: an easy way to recall incompressible flow is through 'IN' for 'INvariable density.'
What happens when there's an increase in velocity in incompressible flow?
Good question! In incompressible flow, changes in velocity do not affect density. Density can be thought of as 'set in stone.'
To sum it up, remember the equations governing these two flows as a primary factor in fluid mechanics.
Mass Conservation Equation
Unlock Audio Lesson
Now, let’s dive into mass conservation equations. Who can remind me what the mass conservation equation states?
It states that mass can neither be created nor destroyed!
Correct! For a control volume, if we apply this to incompressible flow, we have the change in mass is equal to the divergence of mass flux equating to zero. Can someone explain how that looks mathematically?
It can be expressed as ∂ρ/∂t + ∇•(ρv) = 0?
Exactly! For incompressible flow, since density is constant, it simplifies into ∇•v = 0. Remember 'divergence' associated with volume change. It's like verifying a net zero mass flow.
In compressible flow, how does that equation change?
The density is no longer constant, so we modify our equations to consider varying densities.
Great summary! Always visualize how density changes affect flow.
Practical Applications of Flow Types
Unlock Audio Lesson
Let’s discuss applications! How do we apply these principles in engineering scenarios?
Incompressible flow can be seen in applications like water supply systems.
And compressible flow would be relevant in discussing the behavior of air in flight or internal combustion engines, right?
Yes! Precisely. We can examine air and fuel mixtures, for instance. When discussing internal combustion engines, we note how these principles directly affect performance.
So when engines compress air, are we looking at compressible flow?
You got it! When density changes significantly, especially under pressure, compressible flow becomes critical.
Always relate these concepts to their applications to secure understanding.
Comparing Incompressible and Compressible Flow
Unlock Audio Lesson
Let's summarize the key differences between incompressible and compressible flow. Who can begin?
Incompressible flow maintains constant density, while compressible flow does not.
If I remember correctly, in incompressible flow, the velocity change can be felt immediately throughout the fluid.
That's right! Whereas in compressible flow, changes take time to propagate, especially under shockwave conditions.
What implications does that have for fluid systems like aircraft?
Excellent connection! It relates to pressure fluctuations and sound waves. This is crucial for designs.
As a takeaway, visualize how compressibility affects your designs and calculations in real contexts.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section discusses the principles of mass conservation in fluid mechanics, contrasting incompressible flow (where density remains constant and divergence of velocity is zero) with compressible flow (where density varies). It explores how these concepts are mathematically expressed and their physical interpretations.
Detailed
Incompressible vs. Compressible Flow
This section provides a comprehensive discussion about two fundamental types of fluid flow: incompressible and compressible flow. Incompressible flow is characterized by constant density, meaning that the effects of pressure changes do not produce significant variations in density. Therefore, the divergence of the velocity field is zero, signifying that mass is conserved without any accumulation or depletion in a control volume.
In contrast, compressible flow involves variations in density, which occurs under the influence of pressure changes, temperature gradients, or other factors. This means the conservation of mass must account for how density changes over time and space. The mathematical representation, derived from the continuity equations, shows the relationship between the mass flow rates into and out of a control volume.
Through examples and derivations, the section delves deeper into applications such as steady-state and transient flows, providing insights into how these principles affect real-world scenarios in fluid mechanics, particularly in engineering applications like IC engines. Understanding the distinction between these two types of flows is essential for engineers and scientists when modeling fluid behavior in various contexts.
Youtube Videos
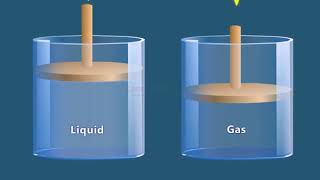
![Compressible and Incompressible Fluids [Physics of Fluid Mechanics #3]](https://img.youtube.com/vi/-vZqSliZzSs/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Understanding Flow Types
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In cases of compressible flow, density can change significantly, leading to variations in mass within a given volume. Conversely, in incompressible flow, density remains constant, and mass flow rates can be evaluated more straightforwardly.
Detailed Explanation
In fluid mechanics, flows can be broadly classified into two categories: compressible and incompressible. Compressible flow involves significant changes in density, typically occurring with gases, especially at high velocities or pressures. This means that as the fluid moves, it may expand or compress, which affects how mass is conserved in certain volumes. On the other hand, incompressible flow assumes that fluid density remains constant, which simplifies calculations, particularly in liquids like water under most conditions. Thus, the fundamental difference is whether or not the density of the fluid can change.
Examples & Analogies
Think of a balloon filled with air as an example of compressible flow: when you pinch it, the volume decreases and the air density increases. Now, consider a water bottle — when you squeeze it, the water doesn’t change density significantly, illustrating incompressible flow.
Mass Conservation in Incompressible Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For incompressible flow, the continuity equation simplifies considerably. It states that the divergence of velocity is equal to zero. This indicates that the mass flow into any small control volume equals the mass flow out, maintaining a constant density throughout.
Detailed Explanation
The continuity equation for incompressible flow is given by the divergence of the velocity vector being equal to zero, represented mathematically as ∇·V = 0. This means that as fluid enters a certain volume, an equal amount must exit, ensuring mass is conserved. The assumption here is that density remains constant, which reduces the complexity of the equations. This principle is crucial in many engineering applications, ensuring systems can maintain a constant flow without accumulating mass.
Examples & Analogies
Imagine a water hose. If water flows in one end at a consistent rate, it must flow out the other end at the same rate (if there are no blockages). This steady flow without change reflects the principles of incompressible flow where the mass is conserved.
Mass Conservation in Compressible Flow
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For compressible flow, density varies along with the mass storage within a control volume. This leads to a more complex continuity equation that takes into account how density changes with fluid motion and time.
Detailed Explanation
In compressible flow, the continuity equation incorporates changes in density, which leads to a more complicated equation: ∂(ρ)/∂t + ∇·(ρV) = 0, where ρ is the density, t is time, and V is the velocity vector. Unlike incompressible flow, this equation indicates that changes in density can lead to variations in how mass is conserved in a given volume. This becomes especially important in analyzing gas flows, such as in jet engines or high-speed aerodynamic tests, where understanding variations in density is critical for accurate predictions.
Examples & Analogies
Consider a bicycle pump: when you push the handle, you’re compressing the air inside the pump, which changes its density. As you push, the amount of air entering corresponds to an increase in pressure, which differs from the incompressible flow where density does not change. This analogy shows how compressible flow behaves uniquely, affecting how we analyze fluid movements.
Practical Implications of Flow Types
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Understanding the characteristics of compressible and incompressible flows is essential for engineers to design systems effectively. Each type of flow can significantly affect performance in applications such as hydraulic systems, aerodynamics, and hydraulic engineering.
Detailed Explanation
Recognizing whether a flow is compressible or incompressible is crucial in engineering applications. For example, in designing a hydraulic system (incompressible flow), the focus might be on ensuring steady pressures and flow rates without major fluctuations. In contrast, for aerospace applications where air is compressible, engineers must consider how changing densities affect lift, drag, and overall vehicle stability. Each type of flow will influence how structures are built, the materials that are chosen, and the calculations needed for successful operation.
Examples & Analogies
Think about air travel: airplanes must be designed considering compressible flow due to the high speeds at which they operate where air density changes significantly. Conversely, the pipes in a dam system operate under incompressible flow conditions, where the design principles focus more on maintaining consistent water pressure and flow.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Density changes are crucial in determining flow characteristics in compressible flow.
-
Incompressible flow is mathematically represented by zero divergence of velocity.
-
Mass conservation must be applied differently in compressible and incompressible flow scenarios.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
When calculating the flow of water through a pipe at constant speed, the flow is typically treated as incompressible.
-
Air moving in a high-speed aircraft can undergo significant compressibility effects, and energy losses due to changes in density are considered.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In incompressible flow, density stays low; compressible changes, as pressures go!
📖 Fascinating Stories
-
Imagine a crowded concert hall, where the volume of people (density) stays the same as they shift around. This is like incompressible flow. Now, think of a balloon; as you squeeze it, it changes density. That's compressible flow!
🧠 Other Memory Gems
-
Remember 'Diverging' for Divergence in fluid context means change. 'In' for Incompressible (no change) and 'Comp' for Compressible (change).
🎯 Super Acronyms
I.C.E. for Incompressible flow Constant density, Compressible flow changes, Energy considerations.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Incompressible Flow
Definition:
A type of fluid flow in which the density of the fluid remains constant despite changes in pressure.
-
Term: Compressible Flow
Definition:
A type of fluid flow where the density of the fluid can change due to pressure and temperature variations.
-
Term: Mass Conservation
Definition:
A principle stating that mass cannot be created or destroyed in a closed system, ensuring the total mass remains constant over time.
-
Term: Divergence
Definition:
A mathematical operator used in fluid flow to measure the net change in density, calculated as the rate at which mass exits a given control volume.
-
Term: Control Volume
Definition:
A fixed region in space used in fluid mechanics analyses to concentrate on the dynamics of fluids.