Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Mass Conservation in Fluid Dynamics
Unlock Audio Lesson
Today, we will start discussing mass conservation in fluid dynamics. Can anyone tell me what mass conservation means?
I think it's about how mass cannot be created or destroyed in a closed system.
Exactly! In fluid mechanics, this principle is foundational. We express it mathematically, particularly through equations for infinitely small control volumes. What would be the parameters we consider in such equations?
We consider density and velocity fields, right?
Correct! Density varies with position and time, while velocity is expressed in its components, u, v, and w. Remember the acronym 'DV' — Density and Velocity. Let's build on this.
What about the Gauss theorem mentioned?
Great question! Gauss's theorem helps us relate volume integrals to surface integrals, which is crucial in deriving these mass conservation equations.
So, are we deriving these equations for incompressible flow?
Yes! For incompressible flow, we assume constant density, leading to what important conclusion?
That the divergence of velocity is zero?
Absolutely! That's a key concept we'll revisit often.
To summarize, today we emphasized the foundations of mass conservation and its implications in fluid dynamics. Remember the DV acronym for future discussions!
Deriving the Mass Conservation Equations
Unlock Audio Lesson
In our last session, we established a foundation for mass conservation. Let's now derive the mass conservation equations from the concepts we discussed. Who remembers the first step?
We start with an infinitesimal control volume, right?
Exactly! This control volume has very small dimensions dx, dy, and dz. By applying the Gauss theorem, we relate the change in mass to the divergence of mass flux. What does this lead us to?
I think it leads to the equation involving density and velocity divergence!
"Correct! We come up with the equation
Applying the Concepts to Different Coordinate Systems
Unlock Audio Lesson
Now that we understand the basic equations, let’s see how we can apply these ideas in different coordinate systems, particularly cylindrical coordinates. What do we need to remember about coordinate transformations?
The coordinates change, but the principles behind the equations remain the same.
"Right! In cylindrical coordinates, we use radial and angular components, which might complicate things slightly. However, the velocity field will still follow the divergence principle.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Velocity divergence is crucial in fluid mechanics, particularly in incompressible flow scenarios. This section discusses mass conservation principles, emphasizing how velocity fields and density interact, leading to significant implications in mathematical modeling and physical applications.
Detailed
Detailed Summary
In fluid mechanics, understanding incompressible flow is essential, particularly concerning the velocity divergence in relation to mass conservation. This section introduces the concept of mass conservation equations for infinitesimal control volumes, derived using Gauss's theorem. The velocity field is represented by the scalar components (u, v, w), while density is treated as a scalar function depending on position and time.
The section elaborates on the derivation of mass conservation equations, demonstrating that the change in mass within a volume equates to the divergence of mass flux at the control surface, leading to the equation
$$\frac{\partial \rho}{\partial t} + \nabla \cdot \left(\rho \mathbf{v}\right) = 0. $$
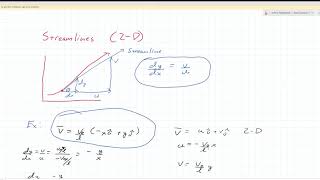
Here, the assumption of incompressibility simplifies these equations because the density remains constant. Therefore, the divergence of velocity is set to zero, leading to the conclusion that
$$\nabla \cdot \mathbf{v} = 0.$$
Further discussion includes recognizing the practical applications of these concepts in cylindrical coordinates and other flow scenarios, which provide a foundation for analyzing fluid behaviors in various engineering contexts. Understanding these principles allows engineers to predict and control fluid movement, making it an essential part of fluid dynamics.
Youtube Videos
![Setting the velocity field to form an incompressible flow [Fluid Mechanics]](https://img.youtube.com/vi/E55ChlbH_5o/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Mass Conservation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In fluid mechanics, the mass conservation equations are used to describe how mass is preserved within control volumes. These equations focus on the changes in mass per unit volume and are essential for analyzing fluid flow. The mass flux is represented as the product of density and velocity.
Detailed Explanation
The concept of mass conservation is fundamental in fluid mechanics. It tells us that within any defined volume of fluid, the amount of mass should neither increase nor decrease unless there is an inflow or outflow of mass. This leads to the formulation of mass conservation equations, which represent how mass changes over time within a control volume. In this context, the mass flux, defined as the product of density (ρ) and velocity (v), quantifies the rate at which mass crosses a surface.
Examples & Analogies
Think of a water balloon. When you squeeze it, the amount of water inside remains the same, but the position of that water changes as it might flow to one side. Similarly, in fluid mechanics, as fluid flows through an area, the total mass must remain constant unless water (or any fluid) is allowed to flow in or out in a measurable way.
Control Volumes and Differentiation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
When we consider control volumes, it is helpful to analyze infinitely small control volumes (dx, dy, dz). By applying Taylor series expansions within these volumes, we can derive relationships for mass conservation.
Detailed Explanation
In fluid mechanics, a control volume is an identifiable region in space where we analyze the mass flow. By examining infinitesimally small volumes—making dimensions dx, dy, and dz approach zero—we can derive precise equations for how fluid moves and how mass changes occur. Taylor series expansions allow us to approximate values at different points in these small volumes, which gives us insights into the fluid behavior at these points and thus helps in formulating the equations governing mass conservation.
Examples & Analogies
Imagine slicing a loaf of bread into very thin slices. Each slice represents an infinitely small control volume of bread, where you can analyze the amount of bread in just that slice without considering the entire loaf at once. By looking closely at each slice, you'll understand how the bread is made and how it moves, similar to analyzing the behavior of fluid in small sections.
Taylor Series and Mass Flux Components
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Using Taylor series expansions at the centroid of a control volume, we can determine the mass flux at different faces of the control volume and express it as rho u for the x-direction, rho v for the y-direction, and rho w for the z-direction.
Detailed Explanation
Taylor series allow us to expand functions about a point, providing polynomial approximations of fluid properties at and around that point. In the context of fluid flow, we can use this series to calculate mass flux components on the different faces of our control volume. For example, mass flux through a face oriented perpendicular to the x-axis is represented by ρu, where ρ is the density and u is the velocity in the x-direction. This process helps us quantify the flow at every surface of our control volume, leading to comprehensive conservation equations.
Examples & Analogies
Consider a faucet that drips water into a bucket. If you place your hand under the drip, you can feel the flow on your skin at various points, which varies based on water pressure and drip speed. This sensation is like the mass flux we measure at different parts of our control volume, where each moment gives a small but clear insight into how water (or any fluid) behaves as it flows together.
Velocity Divergence Implications
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
For incompressible flow, the divergence of the velocity vector field is zero (i.e., div(v) = 0). This means that density remains constant and the flow does not expand or compress.
Detailed Explanation
Incompressible flow is characterized by the fact that the fluid's density does not change. Mathematically, this is expressed as the divergence of the velocity field being equal to zero. When we say div(v) = 0, we're stating that as fluid enters a control volume, the same amount must exit, thereby maintaining a constant density and preventing any compressibility effects. This property simplifies many calculations in fluid dynamics.
Examples & Analogies
Imagine a tube filled with water where you’re trying to push a large ball through the water. As long as the ball can move through without causing any ripple effect across the entire tube (i.e., the water doesn't compress), that flow can be regarded as incompressible. Pressure and density remain constant, much like the constant volume of water moving along the tube.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Mass Conservation: The principle that mass within a closed system remains constant.
-
Divergence of Velocity: A measurement indicating the expansion or compression behavior of the velocity field.
-
Incompressible Flow: Flow characterized by constant density, leading to the zero divergence condition.
-
Control Volumes: A defined region where mass and energy exchanges are analyzed.
-
Cylindrical Coordinates: A method for analyzing fluid flow where dimensions are defined in terms of radial distance, angle, and height.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of fluid flow through a pipe where the density remains constant, validating the principle of incompressible flow.
-
Application of velocity divergence in designing hydraulic systems where ensuring constant flow rate is crucial.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In incompressible flow, where density stays the same, zero divergence is the name of the game.
📖 Fascinating Stories
-
Imagine a closed balloon that doesn't change size. The air inside shifts and flows, but its mass-wise lies. This reflects how fluids in pipes or streams behave, conserving their mass, keeping them safe.
🧠 Other Memory Gems
-
Divergence leads to flow conclusions – remember 'D-Flow!' (Divergence flows to outcomes).
🎯 Super Acronyms
Use 'DVE' for remembering
- D: for Density
- V: for Velocity
- E: for Equations of motion.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Mass Conservation
Definition:
A principle stating that mass cannot be created or destroyed in a closed system.
-
Term: Divergence
Definition:
A measure of the rate at which a quantity expands from a given point.
-
Term: Velocity Field
Definition:
A vector field that represents the velocity of fluid particles at various points in space.
-
Term: Control Volume
Definition:
A defined region in space where mass flow and properties are analyzed.
-
Term: Incompressible Flow
Definition:
Flow in which the fluid density remains constant regardless of pressure changes.
-
Term: Gauss's Theorem
Definition:
A mathematical theorem that relates the flow of a vector field through a surface to the behavior of the field inside the volume.
-
Term: Cylindrical Coordinates
Definition:
A three-dimensional coordinate system that uses a radius, angle, and height to specify a point in space.