Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Control Volumes
Unlock Audio Lesson
Good morning, class! Today, we will explore the concept of control volumes in fluid mechanics. Has anyone heard of this term before?
I think it has something to do with how we analyze fluids within a specific area, right?
Exactly! A control volume is a defined space through which fluid can flow. We analyze the mass conservation within these volumes. Now, does anyone know what the mass conservation equation represents?
It probably represents how mass is neither created nor destroyed within that volume.
That's correct! We can express this mathematically. The equation is essentially a balance between mass inflow and outflow.
How do we derive this equation, though?
Great question! We will dig deeper into that later, but first, let's look at density and velocity.
Mass Conservation Equation Derivation
Unlock Audio Lesson
Let’s start deriving the mass conservation equation. When we have a small control volume of dimensions dx, dy, and dz, we look at how the mass is conserved.
Are we considering the time factor here?
Yes! Mass can change over time as well. We use density ρ as a function of space and time. Let’s remember the acronym FOM: Function Of Mass. This will help us remember that mass is not static.
So how does this relate to the divergence of the mass flux?
Good connection! The change in mass within the volume is equivalent to the divergence of the mass flux. Think of it as a net mass inflow minus outflow.
And this is crucial for understanding fluid dynamics, right?
Absolutely! Understanding control volumes and mass conservation helps in predicting how fluids behave in different situations.
Application of Taylor Series
Unlock Audio Lesson
Next, we apply the Taylor series to approximate how variables change over the control volume. Why do you think this is useful?
It helps us to simplify our equations by focusing only on the initial terms!
Exactly! By ignoring higher-order terms, we simplify calculations and retain accuracy. Remember, it’s FOCUS: First-order Control for Understanding Simplicity.
And that makes it easier to derive important equations?
Yes! This is a common technique used in fluid mechanics.
Incompressible vs. Compressible Flow
Unlock Audio Lesson
Now, let's discuss compressible versus incompressible flows. Who can tell me the difference between the two?
I think incompressible flow has a constant density!
Yes! Incompressible flow assumes density does not change, while compressible flow considers density as a variable. Remember this: CDD - Constant Density Dynamics for incompressibility.
So in compressible flow, we can't ignore changes in density over time?
Right! Incompressible flow reacts instantly to changes throughout the domain, while compressible flow may create shock waves.
Real-World Applications
Unlock Audio Lesson
Finally, let’s look at some real-world applications of these concepts. Can anyone think of examples?
Internal combustion engines use these principles, right?
Yes! They apply mass conservation during fuel combustion processes. Let's use this aid: ICE - Internal Combustion Efficiency, to remember its importance.
What about piping systems?
Great example! Analyzing fluid flow through pipes requires understanding these principles of mass conservation.
I see how crucial this is in engineering!
Exactly! Understanding control volumes and mass conservation equations allows engineers to design better systems.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, we investigate control volumes, emphasizing the balance of mass within these volumes. The section describes how to derive the mass conservation equations using Taylor series and highlights the significance of divergence in describing mass flux and storage changes.
Detailed
Understanding Control Volumes
In fluid mechanics, the concept of control volumes is fundamental for analyzing fluid behavior over specific spaces. This section details how to derive mass conservation equations for infinitesimally small control volumes defined in three-dimensional Cartesian coordinates. We begin by exploring the definitions of density ( ho, velocity components (u, v, w), and their time dependency.
Using the Gauss theorem, we establish that the change in mass within a control volume is related to the divergence of the mass flux. Here, the mass storage change per unit volume equals the net outflux of the mass through the control surface.
We adopt Taylor series expansions for variables changing over space and time, focusing on their behavior at the center of the control volume. This derivation leads us to understand that the mass conservation equations can be simplified effectively, which emphasizes the importance of velocity divergence in incompressibility.
The application of these equations extends to various coordinate systems, allowing the study of mass conservation in cylindrical coordinates as well.
Ultimately, we address the distinct characteristics of compressible versus incompressible flows, illustrating how to effectively apply mass conservation principles in real-world engineering problems.
Youtube Videos
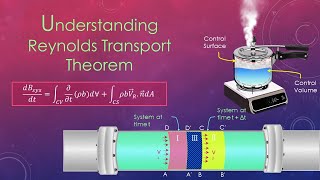
![System Approach and Control Volume Approach [Fluid Mechanics]](https://img.youtube.com/vi/quK9rvsZTPA/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Let us start on the continuity equations. The basically mass conservation equations, mass conservations for infinitely small control volumes as we discuss it that means the control volumes what we consider it, its the dimensions dx dy dz they are very very close to the 0.
Detailed Explanation
Control volumes are essential in fluid mechanics as they help in analyzing the flow of fluids through a defined space. When we refer to 'infinitely small control volumes', we are considering spaces so small that their dimensions (dx, dy, dz) approach zero. This simplification allows us to examine fluid behavior at specific points, making it easier to derive important equations, particularly the continuity equations, which are focused on mass conservation.
Examples & Analogies
Imagine you are watching a small stream of water flowing through a narrow pipe. To understand how much water is flowing at a particular spot, you decide to look at a very tiny segment of the pipe rather than the whole thing. By observing this tiny segment, you can analyze how water enters, moves through, and exits that section, similar to how control volumes help us study fluid dynamics.
Mass Density and Velocity Fields
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So when you have the control volumes infinitely small in that case we are looking at how we can have a differential equations format for mass conservation equation. As we derive it the basically when you have a basic components like we are looking for rho is a density field which is a scalar quantities functions of positions x, y, z in a Cartesian coordinates, then you have the time component. Then we have the time component, v is the velocity field.
Detailed Explanation
In fluid mechanics, mass density (ρ) represents how much mass is contained in a unit volume of fluid, while the velocity field (v) describes how fluid particles are moving in space. Both density and velocity can vary with position (x, y, z) and time. By incorporating these variables into our equations, we can create differential equations that model how mass behaves within our control volumes under different conditions.
Examples & Analogies
Consider a balloon filled with air. The density of the air inside the balloon represents ρ, which can change if you squeeze the balloon or let some air out. Meanwhile, the speed at which the air moves when you release it can vary depending on where you are observing—the surface of the balloon versus the center. This captures how velocity varies in different regions of the fluid.
Application of Gauss's Theorem
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So for considering that through the Gauss theorem concept we try to created basic equations in this format. That is what indicating for us there is a two component in this basic equations. Now one of the component is if you look at this part in any control volumes you have change of the mass components per unit volume. That is what is coming as root by T.
Detailed Explanation
Gauss's theorem relates the flow of a quantity through a surface to the behavior of that quantity in the volume enclosed by the surface. In the context of fluid flow, it allows us to understand how changes in mass within a control volume are related to the flux of mass across its boundaries. This helps to derive fundamental equations in fluid dynamics, particularly the continuity equation for mass conservation.
Examples & Analogies
Think of a balloon again. If you let go of the balloon and it shoots up into the air, air is leaving the balloon through its surface and moving into the wider atmosphere. We can analyze how the amount of air inside (the mass) is decreasing over time based on how quickly air is escaping (the flux). This is similar to how Gauss's theorem helps analyze mass movement through control volumes.
Mass Storage and Flux Balance
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is what indicating for us change of the mass storage within the control volume. That is what will be equal to the divergence of the mass flux within the control volume. This is what we derived from the Gauss theorems for a control volumes.
Detailed Explanation
The concept of mass storage refers to the amount of mass that remains within the control volume over time. When analyzing the mass conservation of a control volume, we find that the change in mass storage within the volume is equal to the difference between the mass entering and exiting the volume. This relationship follows from Gauss's theorem and is foundational to deriving the continuity equation.
Examples & Analogies
Picture a water tank that is filling up and has an outlet at the bottom. The water level (mass storage) inside the tank will change depending on how quickly water is coming in through the pipe compared to how quickly it is going out through the drain. If more is coming in than going out, the water level rises (mass storage increases). This is a practical example of mass storage and flux balance.
Taylor Series Expansion in Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Here the very basic things is that I can apply the Taylor series which it is a very basic concept that any functions if it is a continuous variable then we can approximate using Taylor series expansions.
Detailed Explanation
The Taylor series is a mathematical tool that helps us approximate complex functions. In fluid dynamics, we can use Taylor series to express changes in fluid properties (like velocity or density) at different points in the control volume based on their values at a known point. This approximation allows us to simplify equations and analyze flow behavior more easily.
Examples & Analogies
Imagine you're trying to predict the height of a bouncing ball after a few seconds. Instead of measuring every bounce, you can use a basic equation (like the height at the last bounce) and simple changes (like how much it bounces back) to estimate future heights. This is akin to using a Taylor series to predict fluid behavior based on known properties.
Net Mass Flow Rate
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So we know the inflow max. also the outflux mass. That is what is presented here.
Detailed Explanation
The net mass flow rate through a control volume can be understood as the difference between the total mass flowing into the volume and the total mass flowing out. By calculating the inflow and outflow rates, we gain insights into how mass is conserved within the control volume and can derive the continuity equation.
Examples & Analogies
Consider a water park where a water slide has a catch basin. Water pours into the catch basin faster than it can overflow, so the net flow rate helps managers see how much water is available for additional rides. This analysis is similar to understanding the net mass flow rate in our control volumes.
Conclusion on Control Volumes
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
This is what mass flux in x directions. This is the mass flux in y directions. This is what in z directions.
Detailed Explanation
In summary, the understanding of control volumes and the related principles of mass flux in various directions (x, y, z) is crucial in fluid dynamics. By analyzing how mass flows in and out of a control volume, we can derive important equations that describe fluid behavior and facilitate solving complex fluid dynamics problems.
Examples & Analogies
Just like analyzing how traffic flows in and out of a parking lot at a mall helps in managing space and congestion, understanding mass flow in control volumes helps us manage and predict fluid flow in different applications like engines, pipes, or natural systems.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Control Volume: A defined space for analyzing fluid flow.
-
Mass Conservation: The principle that mass cannot be created or destroyed.
-
Density (ρ): The mass per unit volume of a fluid.
-
Divergence: A mathematical operation measuring the spread of fluid flow.
-
Taylor Series: A series expansion used to approximate variables in calculations.
-
Incompressible Flow: Fluid flow with constant density.
-
Compressible Flow: Fluid flow with changing density.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An internal combustion engine where mass conservation applies to fuel and air mixtures.
-
Fluid flow through a pipe system analyzing the mass entering and leaving the control volume.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
In fluid mechanics, don’t throw a fuss, mass stays the same, it’s just a must.
📖 Fascinating Stories
-
Imagine a busy airport; planes (fluids) arrive and depart, but the number of planes at any moment must stay balanced.
🧠 Other Memory Gems
-
FOM: Function Of Mass helps us remember mass conservation equations.
🎯 Super Acronyms
ICE
- Internal Combustion Efficiency highlights applications of mass conservation in engineering.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Control Volume
Definition:
A specified region in space used to analyze fluid behavior and mass conservation.
-
Term: Mass Conservation Equation
Definition:
An equation stating that mass cannot be created or destroyed within a control volume, relating inflow and outflow.
-
Term: Density (ρ)
Definition:
Mass per unit volume, a critical factor in fluid mechanics.
-
Term: Divergence
Definition:
A measure of how much a vector field spreads out from a point, used in fluid mechanics to analyze mass flux.
-
Term: Taylor Series
Definition:
A mathematical series used to approximate functions, particularly helpful in fluid mechanics for analyzing variable changes.
-
Term: Incompressible Flow
Definition:
Fluid flow where density remains constant throughout.
-
Term: Compressible Flow
Definition:
Fluid flow where density can change due to pressure variations.