Mass Conservation in Control Volumes
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Control Volumes
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Today, we're starting with the concept of control volumes. Can someone explain what a control volume is?

Isn't it a defined region in space that helps us analyze fluid flow?

Exactly! Control volumes help us examine fluid behaviors by observing what goes in and out. We often use small control volumes, right?

Yes, like infinitely small dimensions to derive equations?

Correct! We're focusing on infinitesimally small control volumes with dimensions dx, dy, dz. This allows us to create differential equations to describe mass conservation.

How does this relate to mass flux?

Great question! The divergence of mass flux represents how mass changes within our control volume. Remember, we can express this relation as the change in mass storage over time.

In summary, control volumes are critical for analyzing fluid flows using mass conservation principles.
Deriving the Mass Conservation Equation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now let's derive the mass conservation equation. How might we start?

We should consider the density as a function of space and time?

Right! We express density as ρ(x, y, z, t) and velocity as v(x, y, z, t). We can apply the Taylor series expansion to approximate values at different surfaces. What do we get from this?

We can estimate the mass flux at each face of our control volume!

Perfect! By using Taylor expansion, we can derive an expression for mass flow rates across these surfaces.

So we end up equating the net mass inflow and outflow to the change in mass within the control volume!

Exactly! This equation encapsulates the fundamental principle of mass conservation.

To recap, we derived our mass conservation equation through the analysis of mass flux using Taylor expansions and accounted for inflow and outflow in our control volumes.
Applications of Mass Conservation
🔒 Unlock Audio Lesson
Sign up and enroll to listen to this audio lesson

Now that we've established our equations, can anyone think of where we apply these concepts?

I believe it's used in engineering scenarios like pipe flow and combustion engines?

Correct! Mass conservation helps us predict how fluids behave in different systems. What about further implications?

It can help determine flow rates and pressure changes in systems using compressible and incompressible flow theories!

Exactly! Understanding these applications enables engineers to design effective fluid systems.

Thus, mass conservation is at the core of many engineering applications, ranging from aerodynamics to hydraulic systems.
Introduction & Overview
Read summaries of the section's main ideas at different levels of detail.
Quick Overview
Standard
The section delves into the fundamentals of mass conservation within infinitesimally small control volumes in fluid mechanics, elucidating how variations in mass density and flux are derived from the continuity equations. Emphasis is placed on the application of Gauss's theorem and Taylor series to formulate the mass conservation equations, which are crucial for understanding flow behaviors in a variety of engineering applications.
Detailed
In fluid mechanics, mass conservation is fundamental and is described by the continuity equations, which address mass changes in control volumes. This section begins by introducing control volumes, defined as infinitesimally small dimensions (dx, dy, dz), allowing the derivation of mass conservation equations in differential formats. The density field (ρ) is expressed as a function of spatial coordinates (x, y, z) and time (t), while the velocity field (v) has its components as functions of the same variables. Through Gauss's theorem, we establish that the change of mass within a control volume per unit volume is equal to the divergence of mass flux. This leads to the conclusion that net mass flow rates into the control volume must equal the change in mass storage. The derivation employs Taylor series to approximate fluxes at different volume faces. Consequently, the section reinforces understanding of mass continuity in different coordinate systems and presents practical examples to visualize the application of these theoretical concepts in engineering scenarios.
Youtube Videos


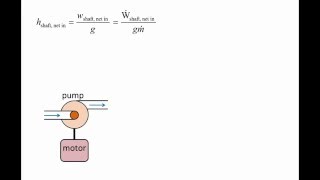




Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Mass Conservation
Chapter 1 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Let us start on the continuity equations. The basically mass conservation equations, mass conservations for infinitely small control volumes...
Detailed Explanation
This section introduces the concept of mass conservation, specifically in relation to fluid mechanics and control volumes. It establishes that we are interested in infinitesimally small control volumes—a mathematical approach that allows us to derive precise equations governing fluid movement. The mass conservation principle states that mass cannot be created or destroyed within a closed system, which is the basis for continuity equations in fluid dynamics.
Examples & Analogies
Think of a small balloon filled with air. Regardless of how much you manipulate the balloon—squeezing it or stretching it—the total amount of air inside stays constant unless you intentionally let air out or blow more air in. This analogy illustrates the basic idea of mass conservation: air can shift within the balloon, but the total mass of air remains unchanged.
Differential Equations for Mass Conservation
Chapter 2 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
...when you have a basic components like we are looking for rho is a density field which is a scalar quantities functions of positions x, y, z...
Detailed Explanation
In this part, the discussion moves toward formulating mass conservation in a mathematical context using differential equations. Density (rho) is introduced as a key variable that varies in space, and various dependent velocity fields (v, u, w) are described. This sets the stage for deriving the mass conservation equation using calculus and vector analysis, indicating how changes in mass density over time can be quantified.
Examples & Analogies
Imagine a small pond where water levels rise and fall due to rain and evaporation. The density of the water remains relatively constant, but the volume changes with rain (input) or evaporation (output). In this analogy, you can think of the pond's surface area as the control volume, showing how the density relates to flow in and out over time.
Application of Gauss' Theorem
Chapter 3 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
...we try to created basic equations in this format. That is what indicating for us there is a two component in this basic equations...
Detailed Explanation
This chunk discusses the use of Gauss' Theorem, which relates the flow of a vector field through a surface to the behavior of the field in the volume enclosed by that surface. In mass conservation, this relates the total mass outflow across the control volume's surface to how mass density changes inside the volume. The two components mentioned are the change in mass storage and the divergence of mass flux, setting up an integral approach to understanding mass flow.
Examples & Analogies
Consider a water pipeline system. If you imagine the water flowing through many pipes, the total amount of water entering a reservoir through these pipes must equal the total amount leaving. In this scenario, the pipes represent the surfaces of a control volume, and Gauss' Theorem helps us ensure that we account for every bit of water moving through these surfaces.
Simplifying Control Volumes
Chapter 4 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Now let us go to the next level instead of looking this vector rotations we can look at a small infinitely small control volumes...
Detailed Explanation
This section explains how to simplify analysis by considering 'infinitely small control volumes' shaped like boxes (parallelepipeds). The speaker emphasizes that by making this simplification, the mathematical analysis becomes much easier while still capturing the essence of fluid behavior. This approach allows for straightforward differential equations that model mass conservation in three dimensions.
Examples & Analogies
Think of examining a single grain of rice in a bowl. While you could look at the entire bowl of rice to assess how much you have, focusing on just one grain simplifies your analysis while still representing the total quantity. In fluid mechanics, examining smaller sections (control volumes) allows you to see how local changes affect the whole system.
Using Taylor Series for Approximation
Chapter 5 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
Here the very basic things is that I can apply the Taylor series which it is a very basic concept that any functions if it is a continuous variable then we can approximate using Taylor series expansions...
Detailed Explanation
The focus here is on applying Taylor series expansions to approximate the values of density and velocity at different points within the control volume. Taylor series help us create more complex functions from simpler polynomial equations. By using this approximation, the speaker derives expressions for velocity at different faces of the control volume, ensuring that the calculations account for how density and velocity change across the volume.
Examples & Analogies
Imagine trying to estimate the height of a mountain based on a few measurements at different points on a hiking trail. If you take those points and use a simple curve to estimate the overall height, you are performing a similar operation to a Taylor series expansion—using known values to fill in the gaps where you don’t have measurements.
Mass Flux Calculations
Chapter 6 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
The advantage of these ones, this case we have considered a very complex control volumes as well as the control surface...
Detailed Explanation
In this section, the discussion transitions to calculating mass flux—the flow of mass through surfaces of the control volume. The speaker introduces the idea that you can express these mass flows (in x, y, and z directions) as products of density, area, and velocity. These calculations are crucial for quantifying how much mass enters or exits through the surfaces of the control volume, integral to the mass conservation equations.
Examples & Analogies
Think about water flowing through a water filter. As water enters a filter, it flows through different openings (surfaces), and depending on how densely packed the filter material is (density) and how much water is pushing through (velocity), the total mass of water that flows through can vary. The process of analyzing this flow is akin to calculating mass flux.
Final Form of the Mass Conservation Equation
Chapter 7 of 7
🔒 Unlock Audio Chapter
Sign up and enroll to access the full audio experience
Chapter Content
This is what the change of the mass within the control volume per unit volume...
Detailed Explanation
Finally, the crucial equations of mass conservation in a control volume are presented. The speaker summarizes how all previous discussions coalesce into a coherent equation that represents the balance of mass inflow, outflow, and accumulation within the volume. The result shows that the net change in mass must equal the divergence of the mass flow, reflecting the principles outlined earlier in this chapter.
Examples & Analogies
Similar to monitoring water entering and leaving a reservoir, if inflow matches the outflow over a specific duration, the total mass of water (or density) in the reservoir remains stable. If we suddenly increase inflow without changing outflow, water will accumulate, demonstrating how mass conservation equations govern real systems.
Key Concepts
-
Control Volume: A defined region for fluid analysis.
-
Mass Flux: Represents the mass flow rate through a cross-sectional area.
-
Conservation of Mass: The principle that mass cannot be created or destroyed in a closed system.
-
Divergence: A vector calculus operation measuring the spreading out of a field.
-
Gauss's Theorem: Essential for linking volume properties with surface integrals.
Examples & Applications
Analyzing the flow in a pipeline using mass conservation principles to compute inflow and outflow rates.
Determining the behavior of air-fuel mixtures in an engine's combustion chamber through continuity equations.
Memory Aids
Interactive tools to help you remember key concepts
Rhymes
In a control volume, mass flows in a dance, / With density and flux taking their chance.
Stories
Imagine a riverbank as a control volume; water flows in and out, always balancing the mass that resides there, teaching us about flow and nature's conservation.
Memory Tools
To remember the order of operations: 'D^2G' - Density, Divergence, Gauss for conservation involving details.
Acronyms
C-MD
Control Volume - Mass flux
Density changes; remember
Flash Cards
Glossary
- Control Volume
A specified region in space through which fluid flows for analysis of mass and momentum.
- Mass Flux
The rate of mass flow per unit area, typically represented as ρv.
- Divergence
A measure of the rate at which a fluid expands or compresses within a given control volume.
- Gauss's Theorem
A mathematical theorem that relates the flux of a vector field through a surface to the behavior of the field inside the volume.
- Taylor Series
A mathematical series used to approximate functions through polynomials based on derivatives at a single point.
- Incompressible Flow
A fluid flow pattern where density remains constant and does not change with pressure.
- Compressible Flow
A flow where the fluid density can change significantly, especially with variations in pressure and temperature.
Reference links
Supplementary resources to enhance your learning experience.
