Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Friction Factors
Unlock Audio Lesson
Today, we are going to discuss friction factors and their importance in calculating head loss in pipes. Can anyone tell me what a friction factor is?
Is it a coefficient that represents the resistance of the flow due to friction against the pipe walls?
Exactly! The friction factor is crucial in determining how much energy is lost as fluid moves through a pipe. We often use this factor in the Darcy-Weisbach equation. What do you think the typical value is for smooth pipes?
It can be around 0.02 or even lower, right?
Yes! For rougher pipes, it can be higher. Remember, roughness affects velocity and flow. Mnemonic tip: 'Flow is slow if the factor is high.' Now, let’s dive into the data given.
Applying the Darcy-Weisbach Equation
Unlock Audio Lesson
We have data: a friction factor of 0.04, a pipe length of 2000 m, and a diameter of 0.2 m. Who can remind us what the Darcy-Weisbach equation looks like?
It’s h_f = f * (L/D) * (v² / (2g)) where h_f is head loss, L is length, and D is diameter.
Great! We’ll also need to calculate the velocity of the water. How would you find that?
We can rearrange the equation or use given total head loss to backtrack the velocity!
Exactly! Now, let’s apply the values and calculate h_f. And remember for head losses: the entry loss coefficient is 0.5 and the exit is 1.
Importance of Loss Coefficients
Unlock Audio Lesson
What do you all think about the role of loss coefficients in our calculations?
They really matter! They can drastically change the results depending on whether we account for them or not.
Plus, we need to consider additional losses due to components like valves and fittings.
Exactly! Entry and exit conditions vary, and every coefficient represents a potential energy loss that must be considered for accurate calculations in designs. Remember: 'Don’t forget to factor in your losses!'
Real-World Applications
Unlock Audio Lesson
Finally, let’s talk about how these calculations influence real-world scenarios such as pumping systems. Why do we need to compute energy required for pumps?
To ensure we have enough power to overcome losses and move the fluid through the system!
Right! So if we find a total head loss, how can we approach the power calculation for a pump?
We use the equation P = ρgQh where Q is flow rate and h is head loss.
Perfect! So always ensure to include your head calculations for realistic pump designs. Let’s wrap up today’s session with a summary!
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The focus is on the application of the Darcy-Weisbach equation to calculate energy losses in pipe flow, highlighting the importance of understanding loss coefficients for entry and exit points. Key given data includes friction factor, length, diameter, and total head loss.
Detailed
Detailed Summary
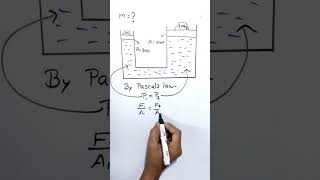
In this section, we introduce essential data and assumptions necessary for analyzing fluid flow through pipes, particularly focusing on the friction factor and head losses. We begin with provided parameters: a friction factor of 0.04, a pipe length of 2000 m, a diameter of 0.2 m, and a total head loss of 8 m. Entry loss coefficients are considered at 0.5, while exit losses are regarded as negligible (1).
The Darcy-Weisbach equation is then applied to compute energy loss due to friction within the pipe and other minor losses that may occur at bends, elbows, and valves. Understanding these coefficients is critical, as they significantly influence how we interpret results and design systems involving fluid flow. By substituting the known values into the equation, we can calculate velocity and ultimately determine the energy requirements for transporting fluids through pipe systems, making this section a foundational component for understanding fluid mechanics in practical applications.
Youtube Videos
![Common assumptions in fluid mechanics [Fluid Mechanics #3b]](https://img.youtube.com/vi/kimMbNP9DrY/mqdefault.jpg)
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Friction Factors and Pipe Data
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
So the friction factors data what is given it length of the pipe the diameters and total head losses.
Detailed Explanation
In fluid mechanics, the friction factor is a crucial parameter used to determine the major energy losses due to friction in pipe flows. The data provided includes the length of the pipe, its diameter, and the total head losses experienced within the system. Understanding these parameters allows for accurate calculations of flow behavior within the pipe.
Examples & Analogies
Imagine you're riding a bicycle on different surfaces. If the bike tires are on a smooth road, you'll glide easily, like water flowing through a big, smooth pipe. But if you're on a gravel path, it becomes harder to pedal, similar to water encountering friction in a narrow, rough pipe. The distance traveled and the type of surface affect how much energy (or head) you need to apply to keep going.
Loss Coefficients at Entry and Exit
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
The loss coefficient in terms of velocity head as you know it at the exit we consider as 1, at the entry we consider 0.5.
Detailed Explanation
Loss coefficients represent the energy losses that occur when fluid enters and exits a pipeline. At the exit, the coefficient is set to 1, indicating a direct relation to the velocity head. At the entry, a coefficient of 0.5 is used, signifying that some energy is lost as the fluid transitions into the pipe. These coefficients are vital for calculating total head loss throughout the system.
Examples & Analogies
Think of the entry and exit of a slide at a water park. When you enter the slide, you lose some speed right away as you start, similar to the 0.5 loss coefficient at the entry. By the time you reach the bottom and exit into the pool, you're moving at a certain speed again, representing the exit coefficient of 1. Some speed is lost in the transition, just like water loses energy entering and exiting a pipe.
Darcy-Weisbach Equation Application
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Now we apply the Darcy Weisbach equations to compute what is energy losses for the major losses or the pipe flow because of the frictions components and the minor losses.
Detailed Explanation
The Darcy-Weisbach equation is a fundamental equation in fluid mechanics used to calculate head loss due to friction in a pipe. It accounts for both major losses (long distances through the pipe) and minor losses (fittings, bends, and other elements). By applying the friction factors and the relevant parameters, we can derive the energy losses that affect the fluid's performance.
Examples & Analogies
Consider a long water slide at an amusement park. The friction between the water and the slide creates resistance (similar to major losses), and there are points where the slide curves or has jumps (minor losses). The Darcy-Weisbach equation helps you calculate how much energy you lose as you go down that slide, just as it helps calculate head loss in a pipe system.
Head Loss Calculation
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
By substituting these and we can get it the series of equations like this and substituting the value you will get a quadratic functions and solving that you will get the velocity.
Detailed Explanation
After setting up the Darcy-Weisbach equation with the appropriate values, solving these values often results in quadratic equations that can be solved for the velocity of fluid flow in the pipe. This step is essential for understanding how quickly the fluid traverses the system and how losses affect this velocity.
Examples & Analogies
Imagine you're baking a cake. Following a recipe (similar to following the equations) and mixing the ingredients leads to a batter that rises. If you get the ratios wrong, the cake won't rise as expected (similar to how the fluid might not flow as expected if losses aren't accounted for). Just like adjusting the ingredients can fix baking issues, solving the Darcy-Weisbach equation helps you find the right flow velocity despite losses.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Friction Factor: Used to calculate energy loss due to friction.
-
Head Loss: Represents total energy loss in a fluid flow scenario.
-
Darcy-Weisbach Equation: Fundamental equation for calculating head losses in pipes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Example of calculating the head loss in a pipe using given parameters.
-
Example of determining pumping power requirements based on total energy losses.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
Friction’s a foe, in pipes it can show, high factors can make your flow slow!
📖 Fascinating Stories
-
Imagine a long water slide where the rough areas slow down the water. The smoother sections keep your ride quick while the rough ones, like entry points, add energy loss.
🧠 Other Memory Gems
-
Remember 'FLAME' for important factors: Friction, Losses, Area, Minor losses, Exit conditions.
🎯 Super Acronyms
PUMP - Power, Up to the Max Potential related to head requirements.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Friction Factor
Definition:
A coefficient representing the resistance to flow due to friction in a pipe.
-
Term: DarcyWeisbach Equation
Definition:
An equation used to calculate head loss due to friction in a pipe.
-
Term: Head Loss
Definition:
The energy loss of the fluid due to friction and other factors.
-
Term: Loss Coefficient
Definition:
A dimensionless coefficient used to quantify the losses in a system component.