Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skills—perfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
You’ve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take practice test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Estimation Methods
Unlock Audio Lesson
Today, we're discussing how to estimate mean precipitation and why it's important for water resource management. Do any of you know why we can't just use data from one rain gauge?
Because rainfall can vary a lot from place to place?
Exactly! Since precipitation is not uniform, especially across different terrains, we need several methods to estimate an average. Let's start with the first method, the Arithmetic Mean Method. It's simple and quick to use. Who can describe when we might use it?
When the rainfall is pretty much the same everywhere, right?
That's correct! It's useful when gauges are evenly distributed and there’s little variability in rainfall.
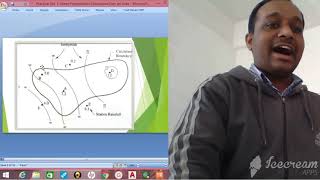
Thiessen Polygon Method
Unlock Audio Lesson
Now let’s explore the Thiessen Polygon Method. Why do you think this method is beneficial for areas with uneven gauge distribution?
Because it uses the proximity of each gauge to divide the area?
Exactly! We form polygons around stations to give more weight to those that are closer to certain areas. What are some limitations of this method?
It assumes rainfall is uniform within the polygon, which might not be true?
Good point! It can lead to inaccuracies if the rainfall varies significantly within the polygons.
Isohyetal Method
Unlock Audio Lesson
Finally, let’s examine the Isohyetal Method. Can anyone tell me how this method improves accuracy?
It considers not just the amount of rainfall, but the variation across different areas, right?
Exactly! By drawing isohyets—lines connecting equal rainfall amounts—we can capture the spatial variability in precipitation. What might be a drawback of this method?
It likely takes more time and skill to interpret the data?
Yes, it does. It requires detailed data and mapping skills, which might not always be available.
Choosing the Right Method
Unlock Audio Lesson
So, how do we decide which method to use? What factors do we need to consider?
The size of the area and how many rain gauges we have?
Right! We also need to consider the topography—steep terrains might require more detailed methods. Remember the acronym S.G.T. for Size, Gauges, and Terrain. Who can summarize what we discussed so far about method selection?
We start with Arithmetic Mean for uniform areas, use Thiessen for uneven distribution, and Isohyetal for complex terrains.
Perfect! Understanding the context ensures more accurate precipitation estimates.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, different conditions are presented to guide the selection of methods for estimating mean precipitation, including the arithmetic mean, Thiessen polygon method, and isohyetal method. The factors influencing the selection include the uniformity of rainfall distribution, the distribution of gauges, and the terrain complexity.
Detailed
Selection of Method
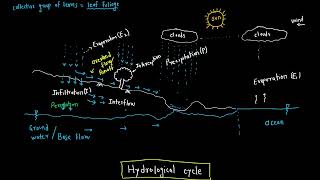
The estimation of mean precipitation over an area is critical for hydrological applications. This section identifies the conditions under which specific methods for estimating mean precipitation should be utilized:
- Arithmetic Mean Method: Recommended when rainfall is uniform and the rain gauge stations are evenly distributed.
- Thiessen Polygon Method: Suitable for situations where gauge distribution is uneven, and there’s moderate variability in rainfall.
- Isohyetal Method: Best used in regions exhibiting high variability in rainfall and complex terrain.
Additionally, when selecting a method, key factors to consider include the size and topography of the area, the distribution and number of rain gauges, as well as the availability of contour data and rainfall records. Each method has unique advantages and limitations, making the correct selection essential for accurate hydrological assessments.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Preferred Methods Based on Rainfall Conditions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Condition Preferred Method
- Uniform rainfall and evenly distributed gauges: Arithmetic Mean
- Uneven distribution of gauges, moderate variation: Thiessen Polygon
- High variability in rainfall, complex terrain: Isohyetal Method
Detailed Explanation
This chunk outlines three different methods for estimating mean precipitation based on specific conditions of rainfall and gauge distribution in an area. The Arithmetic Mean method is best for areas with uniform rainfall and well-distributed gauges, as it is simple and quick to compute. When the rainfall is uneven, but the gauge distribution is moderate, the Thiessen Polygon method is recommended, which takes into account the proximity of gauges to various basin areas. Finally, in areas with high variability of rainfall and complex terrain, the Isohyetal Method is favored because of its accuracy in representing spatial differences in rainfall.
Examples & Analogies
Think of it like making a fruit salad: if all your fruits are uniform in size (like uniform rainfall), you can just toss them together without worrying. But if they vary in size and type (like uneven rainfall), you'll need to be strategic—group similar fruits for balanced flavor (Thiessen Polygon). In a complex recipe where fruits vary widely and require specific treatments (like high variability in rainfall in complex terrain), you would use precise measuring tools to ensure the best mix (Isohyetal Method).
Factors to Consider When Choosing a Method
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Factors to consider while choosing a method:
- Size and topography of the area.
- Distribution and number of rain gauges.
- Availability of contour data and rainfall records.
Detailed Explanation
This chunk highlights crucial factors to consider when selecting an estimation method for mean precipitation. The size and topography of an area are important because they determine how rainfall is distributed. A larger area and complex landscape may require methods that account for variability, such as the Isohyetal Method. The distribution and number of rain gauges also matter; more gauges can lead to a better estimation of the mean precipitation. Lastly, the availability of contour data and rainfall records is essential for certain methods, especially those that depend on mapping and the interpolation of rainfall data, like the Isohyetal Method.
Examples & Analogies
Imagine planning a road trip. The size of the area you need to travel through affects how you plan your stops (size and topography). If you have a detailed map of gas stations (distribution of gauges), you can plan efficiently. But if the map is incomplete (lack of contour data), you'll have a harder time figuring out where to stop for gas as you drive through various terrains.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Uniform Rainfall: When rainfall distribution is consistent across an area, making simpler methods applicable.
-
Method Selection: The process of choosing an appropriate estimation technique based on area characteristics and data availability.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
Using the Arithmetic Mean Method to estimate rainfall in a flat, uniform area with evenly spaced rain gauges.
-
Employing the Thiessen Polygon Method in a basin with unevenly distributed gauges, ensuring that areas nearer to gauges receive appropriate weight in calculations.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
🎵 Rhymes Time
-
For rain you see with gauges aligned, the arithmetic mean's the simplest find.
📖 Fascinating Stories
-
Imagine a farmer needing to know how much it rained over a hill. The farmer checks three gauges, but rain didn't fall equally. Using Thiessen, weight from each is tallied, ensuring no area’s been malled.
🧠 Other Memory Gems
-
Remember 'G.A.T.' for Gauge distribution, Area consideration, Terrain complexity when choosing a method.
🎯 Super Acronyms
P.A.T. stands for Proximity and Area for Thiessen, ensuring accurate rainfall averages.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Arithmetic Mean Method
Definition:
A simple averaging method for estimating mean precipitation when rainfall is uniform.
-
Term: Thiessen Polygon Method
Definition:
A weighted average method that accounts for the proximity of each rain gauge station to different areas.
-
Term: Isohyetal Method
Definition:
An advanced method focusing on drawing isohyets to represent areas of equal rainfall.
-
Term: Rain Gauge
Definition:
An instrument used to measure precipitation.