Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Composition of Velocity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome everyone! Today we'll explore the composition of velocity. Can anyone tell me what composition means in this context?
Is it about adding velocities together?
Exactly! Composition of velocity refers to combining two or more velocities acting in different directions to find the resultant velocity. It's like summing up forces!
How do we add them if they are not in the same direction?
Great question! We use vector addition. This allows us to compute the resultant velocity that captures the full effect of all individual velocities. Think of it this way: if you walk north and then east, your overall path isn't just north or east but a combination of both.
So, can you show us how this involves math?
Sure! Let's say one velocity is 30 m/s east and another is 40 m/s north. We would use the Pythagorean theorem to find the resultant velocity. Would you like to try calculating it?
Yes, I would love to!
Awesome! The resultant velocity is β((30)Β² + (40)Β²), which calculates to 50 m/s. The direction can be found using ΞΈ = tanβ»ΒΉ(40/30) which gives us approximately 53.13Β° north of east.
This is really interesting. So all these formulas are tied together!
Exactly! And it all ties into our understanding of motion.
Resolution of Velocity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's shift gears to resolution of velocity. Who can explain what that involves?
Maybe itβs about breaking down velocities?
Right on the mark! Resolution is about breaking down a single velocity vector into its components, typically in horizontal and vertical directions. This is crucial in solving problems where the motion doesn't align directly along our axes.
How do we actually do that?
We use trigonometric functions! For example, if a velocity is V at an angle ΞΈ to the horizontal, we can find its components as: vx = V cos(ΞΈ) and vy = V sin(ΞΈ).
Can you give us an example?
Absolutely! If a plane is flying at 200 m/s at a 40Β° angle, we'd calculate: vx = 200 cos(40Β°) and vy = 200 sin(40Β°). The horizontal component comes to approximately 153.2 m/s while the vertical component is about 128.6 m/s.
That makes it easier to analyze the motion!
Precisely! And thatβs the power of resolution.
Applications in Real World
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we've learned about composition and resolution, letβs discuss some real-world applications. Can anyone think of where these might be used?
Like in sports?
Exactly! In sports, athletes often need to resolve velocities. Think of a basketball player moving in diagonal pathsβunderstanding these components is vital.
What about projectile motion? We talked about it before.
Great connection! In projectile motion, for instance, the horizontal component of velocity remains constant while the vertical component changes due to gravity. This understanding is crucial in calculating paths in sports, engineering, and even space travel.
Can we apply this in motion on inclined planes as well?
Absolutely! When objects move up an incline, their velocities need to be resolved into components parallel and perpendicular to the incline. This allows us to understand the forces acting on the object.
It's amazing how these methods are applicable everywhere!
Indeed! Understanding composition and resolution is fundamental in physics.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
It explains how to combine multiple velocities acting in different directions to find the resultant velocity (composition) and how to break down a single velocity into its components (resolution). Real-world applications include projectile motion and motion along inclined planes.
Detailed
Composition and Resolution of Velocity
Overview
This section delves into the critical concepts of composition and resolution of velocity, two essential principles in kinematics that help in analyzing the motion of objects.
Composition of Velocity
- Definition: The composition of velocity involves adding two or more velocities acting in different directions to find a resultant velocity.
- Vector Addition: When these velocities are not aligned, vector addition is employed to calculate the resultant.
Resolution of Velocity
- Definition: The resolution of velocity is the process of breaking down a vector velocity into its components, typically in perpendicular directions (horizontal and vertical).
- Utility: This simplification aids in solving problems related to motion that do not align with the coordinate axes.
Applications
- The concepts of composition and resolution are widely applicable in scenarios like projectile motion, motion on inclined planes, and relative motion analysis, making them vital for real-world physics.
Youtube Videos
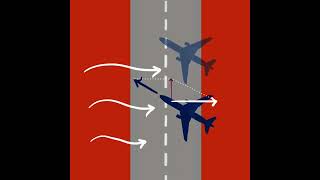
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Introduction to Composition and Resolution of Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Introduction to Composition and Resolution of Velocity
β What is Composition of Velocity?
β The composition of velocity refers to combining two or more velocities acting on an object in different directions. In this process, the individual velocities are added vectorially to determine the resultant velocity.
β In cases where velocities are not acting in the same line or direction, vector addition is used to find the resultant velocity, which is the combined effect of all the individual velocities.
β What is Resolution of Velocity?
β Resolution of velocity involves breaking down a single velocity into its components along different directions, usually perpendicular to each other (e.g., horizontal and vertical components).
β This helps simplify problems in motion when the velocity is not aligned with the axes of the reference frame.
Detailed Explanation
In this introduction, we learn about two primary concepts: composition and resolution of velocity.
Composition of velocity means adding different velocities together to find a single resultant velocity. For instance, if one velocity is moving east and another north, you combine them to find out how fast and in what direction the object overall is moving. Resolution of velocity, on the other hand, is the opposite process: it involves breaking a single velocity into its parts or components, making it easier to analyze motion in different directions, especially when those directions are at right angles to each other.
By having these two concepts, we can analyze more complex motions and understand how an object moves in varying conditions.
Examples & Analogies
Imagine you're riding a bicycle on a windy day. If the wind is pushing you from the east while you're pedaling towards the north, your overall movement needs to account for both the direction you're riding and the direction of the wind. This scenario would require composing the two velocities. Conversely, if you know your overall speed and direction but want to understand how fast you're moving east and how fast you're moving north, you would resolve that single velocity into its two components.
Vector Representation of Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Vector Representation of Velocity
β What is a Vector?
β A vector is a physical quantity that has both magnitude and direction.
β Velocity is a vector quantity because it has both speed (magnitude) and direction. Other vector quantities include displacement, force, and acceleration.
β Components of a Vector
β A vector can be represented in terms of its components along the chosen coordinate axes (usually x and y). For two-dimensional motion:
β Velocity Vector: vβ=vxi^+vyj^
Where:
β vxv_x is the velocity component along the x-axis.
β vyv_y is the velocity component along the y-axis.
β i^ ext{ and }j^ ext{ are unit vectors along the x and y directions, respectively.
Detailed Explanation
Vectors are key to understanding composition and resolution of velocities because they provide a way to express physical quantities that have both a magnitude and a direction. When you have a velocity like 30 m/s east, you not only have a speed (30 m/s), but you also know the direction (east).
Vectors are usually represented in a two-dimensional plane with x and y components. For example, a velocity of 50 m/s at an angle from the horizontal can be split into how much of that speed goes in the horizontal (x-axis) direction and how much goes in the vertical (y-axis) direction. The unit vectors (i and j) help to indicate these directions clearly.
Examples & Analogies
Think of a treasure map. The distance you need to walk to find the treasure can be represented as a vector. If you have to walk 50 meters east and then 30 meters north, those distances are like the components of a vector showing your total journey β not just how far youβre going, but also where you're headed. The unit vectors can be thought of as indicators showing which direction is east and which is north on your map.
Composition of Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Composition of Velocity
β Composition of Velocities in the Same Direction
β When two velocities are acting in the same direction, their resultant velocity is simply the algebraic sum of the magnitudes of the individual velocities. Resultant velocity=v1+v2
Where:
β v1v_1 and v2v_2 are the individual velocities in the same direction.
β Composition of Velocities in Perpendicular Directions
β When two velocities are acting at right angles (perpendicular) to each other, the Pythagorean theorem is used to find the resultant velocity.
vR=v12+v22
Where:
β vRv_R is the resultant velocity.
β v1v_1 and v2v_2 are the two velocities at right angles to each other.
β The direction of the resultant velocity is given by:
ΞΈ=tan β1(v2v1)
Where ΞΈ heta is the angle of the resultant velocity with respect to the horizontal axis (the direction of v1v_1).
Detailed Explanation
Here, we're focusing on how to combine velocities, especially how they add up when they are directed either the same way or at right angles to each other. If two velocities are acting in the same direction, you simply add them together; for example, if you run at 5 m/s east and then 3 m/s east, your total speed would be 8 m/s east.
However, if the velocities are at right angles, like 5 m/s east and 3 m/s north, you use the Pythagorean theorem to find the total or resultant velocity. To understand the direction, you calculate the angle using tangent, which helps you understand how far off the horizontal your new direction is.
Examples & Analogies
Imagine two friends who are running in a competition. One friend runs straight forward while the other runs sideways. If they want to determine how fast they are getting away from a starting point, theyβd need to combine their speeds, which is straightforward if they're going in the same direction. If they're at right angles, it's like finding the shortest path to their new point using a right-angled triangle β taking both their paths into account gives them a clear understanding of their actual speed and direction together.
Example: Composition of Velocities in Perpendicular Directions
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example: Composition of Velocities in Perpendicular Directions
β A car is moving with a velocity of 30 m/s eastward and another 40 m/s northward. To find the resultant velocity:
vR=(30)2+(40)2=900+1600=2500=50 m/s
The direction is:
ΞΈ=tan β1(4030)=tan β1(1.33)β53.13β
Hence, the resultant velocity is 50 m/s at an angle of 53.13Β° north of east.
Detailed Explanation
This example shows how to solve for the resultant velocity when dealing with perpendicular velocities. First, you determine the resultant speed using the Pythagorean theorem, which combines the squares of each perpendicular velocity component. The square root of that sum gives us the resultant speed, 50 m/s in this case. Then, to find the angle of this resultant velocity, we use the inverse tangent function, which helps us derive how far from the east (the x-axis) the resultant vector points; here, it comes out to approximately 53.13 degrees.
Examples & Analogies
Think of a car driving straight along a road and then turning to drive up a hill. The combined speed at which both these motions happen can be visualized as forming a triangle: straight down the road is one side, and up the hill forms another side. By applying the Pythagorean theorem, you determine the overall speed and direction of the car's motion, much like determining a shortcut across town rather than following the streets exactly.
Resolution of Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Resolution of Velocity
β What is Resolution of a Velocity Vector?
β Resolution of a velocity vector refers to the process of breaking a single velocity vector into two components, typically along perpendicular axes, such as horizontal and vertical directions. This is particularly useful in problems involving projectile motion or motion on inclined planes.
β Components of Velocity
β A velocity vector can be broken down into two perpendicular components, typically in the x-direction (horizontal) and the y-direction (vertical):
vx=vcos (ΞΈ)andvy=vsin (ΞΈ)
Where:
β vv is the magnitude of the velocity.
β ΞΈ heta is the angle the velocity vector makes with the horizontal axis.
β vxv_x is the horizontal component (velocity in the x-direction).
β vyv_y is the vertical component (velocity in the y-direction).
Detailed Explanation
Resolution involves taking a total velocity and breaking it down into parts that are easier to work with. When we analyze a motion that is not aligned with our reference directions (horizontal and vertical), we can find the x and y components by using trigonometry. The formulas vx = v cos(ΞΈ) and vy = v sin(ΞΈ) help us calculate how much of the overall velocity goes in the horizontal direction and how much goes in the vertical direction. This separation is essential for analyzing motion dynamics correctly, particularly in scenarios like projectiles or objects on a slope.
Examples & Analogies
Imagine a basketball player shooting the ball towards the hoop at an angle. To understand the ball's motion, we can break its movement into two parts - how high it goes (the vertical motion) and how far it goes horizontally. These components help coaches analyze the shot's success, much like knowing how to resolve different aspects of a playerβs performance helps in coaching decisions.
Example: Resolution of Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Example: Resolution of Velocity
β Suppose an object moves with a velocity of 40 m/s at an angle of 30Β° above the horizontal. To find the components:
vx=40cos (30β)=40Γ32β34.64 m/s
vy=40sin (30β)=40Γ12=20 m/s
So, the horizontal component of velocity is approximately 34.64 m/s, and the vertical component is 20 m/s.
Detailed Explanation
In this example, we calculate the horizontal and vertical components of a velocity that is directed at an angle. By applying the trigonometric formulas, we find that approximately 34.64 m/s contributes to the horizontal direction, while 20 m/s goes into the vertical direction. Understanding these components gives us a clearer insight into the object's behavior in a plotted motion path, as it reveals how much of the velocity impacts each axis.
Examples & Analogies
Think about launching water from a garden hose. If you angle the hose at 30 degrees, some of that water will shoot up (vertical motion), while some will move forward (horizontal motion). The easier you can separate these two forces, the better you can adjust your hose angle to get water where you want it!
Applications of Composition and Resolution of Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Applications of Composition and Resolution of Velocity
β Projectile Motion
β In projectile motion, the velocity of the object is resolved into two components: one horizontal and one vertical. The horizontal component remains constant (assuming no air resistance), while the vertical component changes due to gravity.
β Motion on Inclined Planes
β When an object moves along an inclined plane, the velocity is resolved into two components: one parallel to the incline and one perpendicular to it. The parallel component is responsible for the motion along the incline, while the perpendicular component is balanced by the normal force.
β Relative Motion
β In problems involving relative motion, the velocities of two objects moving relative to each other are often composed or resolved. For instance, the velocity of a moving object relative to a stationary observer can be found by combining the velocity of the object and the observer.
Detailed Explanation
These concepts find broad applications in real-world physics. For instance, in projectile motion, understanding how the velocity of a thrown object breaks into horizontal and vertical components is crucial for calculations regarding how far and high the projectile will go, especially in sports or engineering.
In inclined planes, such as ski slopes, knowing how gravity affects the movement allows designers to create safer slopes. Similarly, understanding relative motion is essential in a variety of contexts, like calculating one vehicleβs speed with respect to another or a boat in a river that has a current.
Examples & Analogies
Consider throwing a basketball towards a hoop; understanding the balance between how high it goes and how far it travels horizontally helps ensure you make the shot. In navigation, pilots also consider wind speeds to help them calculate their actual travel speed, ensuring they arrive at their destination on time.
Conclusion
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Conclusion
β Summary of Key Points
β Composition of velocity involves combining two or more velocities in different directions to find the resultant velocity, which is done using vector addition.
β Resolution of velocity is the process of breaking down a velocity vector into two perpendicular components (typically horizontal and vertical).
β These concepts are widely used in projectile motion, inclined plane motion, and relative motion problems.
β Practical applications include navigation, sports, and the study of various physical systems involving motion.
Detailed Explanation
The conclusion summarizes the major takeaways: Composition of velocity helps us add vectors to find overall movement, while resolution allows us to dissect that movement for better understanding. The significance of these concepts cannot be understated, as they are foundational in fields ranging from physics to engineering and are applicable in everyday scenarios like driving, sports, and navigation.
Examples & Analogies
Think about a game of soccer, where players must constantly gauge both their speed and direction relative to the ball and other players. Composing and resolving velocities helps players pass effectively or avoid opponentsβand mastering this can make the difference between winning and losing in an actual game.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Composition of Velocity: Combining multiple velocity vectors to determine a resultant velocity using vector addition.
-
Resolution of Velocity: Breaking down a single velocity vector into its components along perpendicular directions.
-
Resultant Velocity: The final outcome of combining different velocities, calculated using vector addition methods.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A car moving 30 m/s east and 40 m/s north results in a velocity of 50 m/s at a 53.13Β° angle from east.
-
A plane flying at 200 m/s at a 40Β° angle has horizontal and vertical components of approximately 153.2 m/s and 128.6 m/s respectively.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
To find the resulting velocity, Pythagoras is key, add the squares you see!
π Fascinating Stories
-
Imagine a bird flying north and east; the result is the diagonal you need to feast. Pythagorean magic helps you find, the direction in which the bird is aligned.
π§ Other Memory Gems
-
For the resolution, remember: SOHCAHTOA - Sine = Opposite over Hypotenuse, Cosine = Adjacent over Hypotenuse.
π― Super Acronyms
V.R.C - Velocity Resolution Components
- V: for Velocity
- R: for Resolution
- C: for Components!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Velocity
Definition:
A vector quantity that describes the speed and direction of an object's motion.
-
Term: Vector
Definition:
A quantity possessing both magnitude and direction.
-
Term: Resultant Velocity
Definition:
The overall velocity achieved by combining two or more velocities acting simultaneously.
-
Term: Resolution of Velocity
Definition:
The process of breaking down a single vector into its components along perpendicular axes.
-
Term: Composition of Velocity
Definition:
The operation of combining different velocities acting on an object to find the resultant velocity.