Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Vectors
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Welcome class! Today we're starting with vectors. Can anyone tell me what a vector is?
A vector has both magnitude and direction.
Correct, Student_1! Vectors are essential in physics as they help us describe quantities like velocity. What's one example of such a vector quantity?
Velocity!
Exactly! Now, remember that velocity not only tells us how fast an object is moving but also in which direction. So, let's break down how we can mathematically represent a velocity vector.
Components of a Velocity Vector
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
A velocity vector can be represented in terms of its components along the x and y axes: vβ = vx*i + vy*j. Can anyone explain what vx and vy mean?
vx is the velocity along the x-axis, and vy is along the y-axis.
Right, Student_3! This representation helps us analyze the motion in two dimensions. For example, if a car is moving east at 30 m/s and north at 40 m/s, how would we write this in vector form?
It would be vβ = 30*i + 40*j.
Great job! This decomposition is critical when we move on to composition and resolution of velocities.
Mathematical Representation of Velocity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we know how to write a velocity vector, how do we visualize it? Imagine drawing this on a graph: vx goes along the horizontal axis and vy along the vertical.
So we can represent it graphically?
Exactly! And the resultant vector can be found using the Pythagorean theorem if the components are perpendicular. Can anyone summarize that for me?
We can use sqrt(vxΒ² + vyΒ²) to find the magnitude of the resultant vector!
Spot on! This concept will be crucial as we discuss composition of velocities in different directions.
Further Applications of Velocity Vectors
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs explore how vector representation helps us in real-world scenarios, like in sports or navigation. Why is it important to represent velocity as a vector in these cases?
It helps us understand not just how fast an object is moving, but also where it's heading.
Exactly, Student_3! Knowing both speed and direction can be crucial for decision-making in scenarios like catching a ball in baseball or directing a plane.
So it's like mapping out a path, right?
Exactly! You've captured it perfectly. Understanding velocity vectors ensures effective navigation and movement understanding.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The section explains that velocity is a vector quantity characterized by both magnitude and direction. It covers the representation of velocity vectors in terms of their components along the x and y axes and explains how to express a velocity vector mathematically.
Detailed
In this section, we delve into the vector representation of velocity, explaining that a vector is defined as a physical quantity possessing both magnitude and direction. Velocity, as a vector quantity, is thus described not merely by its speed (magnitude) but by its directional component as well. We introduce the mathematical expression for a two-dimensional velocity vector in the form: vβ = vxi + vyj, where vx and vy represent the components of velocity along the x and y axes, respectively. This framework is fundamental as it allows us to analyze motion in two dimensions efficiently, facilitating further discussions on the composition and resolution of velocities.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
What is a Vector?
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β A vector is a physical quantity that has both magnitude and direction.
β Velocity is a vector quantity because it has both speed (magnitude) and direction. Other vector quantities include displacement, force, and acceleration.
Detailed Explanation
A vector is a type of quantity used in physics that has two essential characteristics: magnitude and direction. Magnitude refers to how much of something there isβsuch as speed or distanceβwhile direction indicates where that quantity is pointing. Velocity is a prime example of a vector because it tells us how fast an object is moving (the magnitude) and in which direction it is moving. Similarly, other quantities like force and displacement are also vectors because they possess both of these attributes.
Examples & Analogies
Think of a vector like giving someone directions to a restaurant. You tell them not just the distance (e.g., 'it's 3 miles away') but also the direction (e.g., 'go north'). Without both pieces of information, they wouldn't reach the restaurant!
Components of a Vector
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
β A vector can be represented in terms of its components along the chosen coordinate axes (usually x and y). For two-dimensional motion:
β Velocity Vector: vβ = v_x i^ + v_y j^
where:
β v_x is the velocity component along the x-axis.
β v_y is the velocity component along the y-axis.
β i^ and j^ are unit vectors along the x and y directions, respectively.
Detailed Explanation
In two-dimensional space, a vector can be broken down into parts that correspond to the x (horizontal) and y (vertical) axes. The notation 'vβ = v_x i^ + v_y j^' shows how we can express the vector v with its horizontal component 'v_x' and vertical component 'v_y'. Here, 'i^' and 'j^' are the unit vectors that indicate directions along the horizontal and vertical axes. This breaking down of vectors into components is crucial for simplifying calculations involved in physics problems, especially in motion.
Examples & Analogies
Imagine you are walking in a park that is laid out in a grid pattern. If you walk 3 blocks east and then 4 blocks north, you can think of your path as a right triangle where the two legs represent your walk east (3) and north (4). If someone asks you how far you are from your starting point straight (as the crow flies), you can use the Pythagorean theorem to calculate that distance, which correlates to the vector representation of your journey.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Vector: A physical quantity that has both magnitude and direction.
-
Velocity: A vector quantity indicating speed with direction.
-
Components of a Vector: Vectors can be broken into horizontal and vertical components.
-
Unit Vectors: Vectors that have a magnitude of one, used to denote direction.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A car moving east at 30 m/s can be represented as v = 30*i.
-
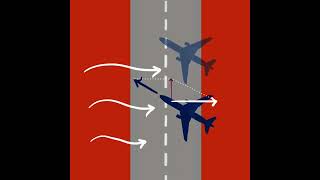
An airplane flying at 200 m/s at a 40Β° angle to the horizontal has velocity components of approximately 153.2 m/s horizontal and 128.6 m/s vertical.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Vectors travel, they can race, / With both speed and direction they embrace.
π Fascinating Stories
-
Imagine a sailor navigating; she uses her compass to find her speed (magnitude) and the direction of her journey (vector).
π§ Other Memory Gems
-
Remember 'V = M + D' to think of Velocity equals Magnitude and Direction.
π― Super Acronyms
V for Velocity, M for Magnitude, D for Direction.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Vector
Definition:
A quantity that has both magnitude and direction.
-
Term: Velocity
Definition:
A vector quantity that describes the rate of change of position with respect to time, incorporating both speed and direction.
-
Term: Magnitude
Definition:
The size or length of a vector, representing its strength or intensity.
-
Term: Component
Definition:
The projections of a vector along the axes of a coordinate system, typically the x and y components.
-
Term: Unit Vector
Definition:
A vector with a magnitude of one, used to specify direction.