Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Understanding Velocity Composition
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we are summarizing what we learned about velocity composition. Remember, when we have multiple velocities acting on an object, how do we find the resultant velocity?
We add them vectorially, right?
Exactly! For velocities in the same direction, we simply add their magnitudes. Now, what about when they're at right angles?
We use the Pythagorean theorem!
That's right! It's vR = β(v1Β² + v2Β²). Can anyone give me an example?
If one velocity is 30 m/s east and another is 40 m/s north, the resultant would be 50 m/s at an angle, right?
Correct! And the direction can be found using ΞΈ = tanβ»ΒΉ(v2/v1). Great summary of the concept! Let's wrap it up.
So to recap: compose velocities by vector addition for the same direction, or use the theorem for perpendicular ones.
Exploring Velocity Resolution
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now let's talk about how we resolve velocities into components. Why is this useful?
It helps with problems when the velocity isnβt aligned with the coordinate axes.
Excellent! We often resolve a velocity into horizontal and vertical components using v_x = v cos(ΞΈ) and v_y = v sin(ΞΈ). Can someone calculate the components if a plane is flying at 200 m/s at 40Β°?
The horizontal component would be about 153.2 m/s and 128.6 m/s vertical.
Correct! Always remember: this breakdown is foundational for understanding motion in multiple contexts.
In summary: breaking down velocities into components allows us to analyze motion effectively in various scenarios.
Application of Concepts
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Finally, how do composition and resolution of velocity play out in real-world applications?
They are crucial for things like projectile motion and navigation!
Absolutely! For example, in projectile motion, we find a horizontal and a vertical component of the initial velocity. Why does this matter?
It helps predict where the projectile will land and its trajectory.
Correct! And on inclined planes, we resolve forces into components to analyze motion accurately. Any thoughts on other fields?
In sports, athletes need to understand these principles too!
Exactly! So remember, the concepts of composition and resolution are not just theoretical, they apply across various fields.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
The conclusion summarizes key concepts of velocity composition and resolution, highlighting their significance in understanding motion in different directions. It notes practical applications in areas such as projectile motion, navigation, and sports.
Detailed
Conclusion
Throughout this chapter, we explored the composition and resolution of velocities, crucial concepts for understanding motion. The composition of velocity entails combining multiple velocities acting in different directions, which is essential for determining a resultant velocity through vector addition. On the other hand, resolution of velocity involves breaking down a single vector into its components, typically along horizontal and vertical axes, simplifying analyses in complex motion scenarios. These principles are widely utilized in various applications, from projectile motion to real-world navigation, underscoring their relevance in both academic and practical contexts.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
Summary of Composition of Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Composition of velocity involves combining two or more velocities in different directions to find the resultant velocity, which is done using vector addition.
Detailed Explanation
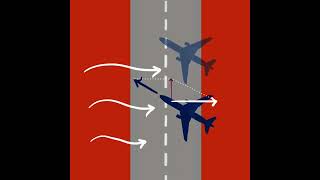
The composition of velocity is a vital concept in physics where we need to combine multiple velocities acting on an object. This is not as simple as just adding the numbers, especially if the velocities are in different directions. Instead, we use a method called vector addition. This method allows us to calculate a single resultant velocity, which is a combination of all those different velocities.
Examples & Analogies
Consider a boat moving across a river. If the boat has a speed of 10 km/h in a straight line across the river but the current of the river pushes it downstream at 5 km/h, we cannot simply add these speeds directly. Instead, we create a triangle of velocities where one side represents the boat's speed and the other represents the river's current. The boat's actual path will then be the hypotenuse of this triangle, showing the actual resultant velocity of the boat in the water.
Summary of Resolution of Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Resolution of velocity is the process of breaking down a velocity vector into two perpendicular components (typically horizontal and vertical).
Detailed Explanation
When we talk about resolution of velocity, we refer to breaking a single velocity vector into two components that are at right angles (perpendicular) to each other. This is particularly useful when analyzing motion in two dimensions, such as projectile motion. By resolving a velocity vector into horizontal and vertical components, we can more easily apply physics laws and solve problems involving motion.
Examples & Analogies
Imagine a basketball player jumping to make a slam dunk. The player's velocity can be split into two parts: one that goes upwards (vertical) and one that goes forward (horizontal). By resolving the player's jumping velocity this way, coaches can better understand how to maximize a player's jump for scoring points. Each component affects the player's ability to reach the basket from different angles.
Applications of Composition and Resolution of Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
These concepts are widely used in projectile motion, inclined plane motion, and relative motion problems.
Detailed Explanation
The applications of composition and resolution of velocity are vast. In projectile motion, for instance, the path of a thrown object can be understood by breaking down its velocity into horizontal and vertical components. In the case of inclined planes, resolution helps us analyze forces acting on an object sliding down. Similarly, understanding relative motion involves composing or resolving velocities to assess how objects move concerning one another, which is crucial in many real-world scenarios.
Examples & Analogies
Think of a soccer ball being kicked at an angle. The ball's curved trajectory can be predicted by examining its horizontal motion (how far it goes) and vertical motion (how high it goes). Coaches often use this understanding when training players so they can optimize their kicking technique based on the desired outcome of the shot. This practical knowledge directly stems from the concepts of composition and resolution of velocity.
Practical Applications of Velocity Concepts
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Practical applications include navigation, sports, and the study of various physical systems involving motion.
Detailed Explanation
Understanding composition and resolution of velocity is not just an academic exercise; it has numerous practical applications. For instance, in navigation, pilots and sailors must compose velocities to chart their routes effectively, taking into account wind and ocean currents. In sports, athletes often use strategies that involve these principles to enhance their performance. Overall, these concepts underpin many physical systems and are vital for navigating the world and understanding it better.
Examples & Analogies
Consider a pilot flying an airplane. The plane's speed relative to the ground is affected by the speed of the wind. The pilot must use composition of velocities to calculate the true heading and speed required to reach the destination efficiently. This means understanding the wind's effect and adjusting the plane's path accordingly.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Composition of Velocity: The process of combining multiple velocities to arrive at a resultant.
-
Resolution of Velocity: Breaking down a velocity vector into its components for analysis.
-
Resultant Velocity: The final velocity derived from the composition of other velocities.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A car moves east at 30 m/s and north at 40 m/s. The resultant is 50 m/s at approximately 53.13Β°.
-
An object is launched at 40 m/s at an angle of 30Β°, with components 34.64 m/s and 20 m/s.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Velocity is full of zest, combine and break, it's for the best!
π Fascinating Stories
-
Imagine two friends running, one north and one east; together they race to find the fastest route home, showing the power of velocity composition.
π― Super Acronyms
C for Combine Vectors, R for Resolve them, V for Visualize motion!
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Velocity
Definition:
A vector quantity that describes the rate of change of an object's position in a specific direction.
-
Term: Composition of Velocity
Definition:
The process of combining two or more velocities to find a resultant velocity.
-
Term: Resolution of Velocity
Definition:
The method of breaking down a velocity vector into its components, typically along perpendicular axes.
-
Term: Resultant Velocity
Definition:
The resultant velocity after composing two or more velocities, taking into account their directions.
-
Term: Vector Addition
Definition:
A mathematical operation that combines two or more vectors to produce a single vector.