Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Velocity and Its Resolution
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today we're going to learn about the resolution of a velocity vector. Can anyone tell me what a velocity vector is?
Isnβt it just how fast something is moving and in what direction?
Exactly! Velocity is a vector, meaning it has both speed and direction. Now, when we say resolution of a velocity vector, what do you think that might mean?
Maybe itβs about breaking it down into parts?
Great point! We break down the velocity into components, usually horizontal and vertical. This helps us simplify our calculations when analyzing motion. Remember: βBreak it down to build it betterβ!
Components and Their Calculation
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Let's talk about how we calculate these components. For a velocity vector making an angle \(\theta\) with the horizontal, we use \(v_x = v \cos(\theta)\) for the horizontal component and \(v_y = v \sin(\theta)\) for the vertical component.
Can you give us an example of that?
Sure! If an object moves with a velocity of 40 m/s at an angle of 30Β°, what would be its components?
For \(v_x\) it would be \(40 \cos(30Β°)\)?
Thatβs correct! And for the vertical component? What do we do?
We would use \(40 \sin(30Β°)\)!
Exactly! So we have \(v_x \approx 34.64 \text{ m/s}\) and \(v_y = 20 \text{ m/s}\).
Applications of Velocity Resolution
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now letβs connect this to real-life applications. Why is resolving velocity useful, especially in projectile motion?
Because the objectβs horizontal and vertical movements can be very different!
Correct! In projectile motion, the horizontal component is constant while the vertical component changes due to gravity. Can anyone think of where else weβd apply this?
How about when a car drives up a hill?
Yes! The velocity has to be resolved into components parallel and perpendicular to the incline. This understanding helps us analyze and predict motion accurately.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
Resolution of velocity involves decomposing a velocity vector into perpendicular components to simplify motion analysis, particularly useful in projectile motion and movement along inclined planes. This allows for clearer calculations of motion in different directions.
Detailed
Resolution of Velocity
Resolution of velocity refers to the systematic breakdown of a velocity vector into two components that are typically perpendicular to each other, such as horizontal (x-direction) and vertical (y-direction) components. This concept is crucial in various physics problems, especially those involving projectile motion and inclined plane motion.
Key Points:
- Components of Velocity: A velocity vector can be decomposed into components using the relationships:
- Horizontal Component: \( v_x = v \cos(\theta) \) where \( v \) is the magnitude of the velocity and \( \theta \) is the angle from the horizontal.
- Vertical Component: \( v_y = v \sin(\theta) \).
- These formulas clarify how much of the velocity is directed along each axis.
- Example: For an object moving with a speed of 40 m/s at an angle of 30Β° above the horizontal, the components can be calculated as follows:
- \( v_x = 40 \cos(30Β°) \approx 34.64 \, \text{m/s} \)
- \( v_y = 40 \sin(30Β°) = 20 \, \text{m/s} \)
This tells us how fast the object is moving horizontally (34.64 m/s) and vertically (20 m/s).
Understanding the resolution of velocity helps in solving real-life problems involving various types of motion by allowing the analysis of each component separately.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
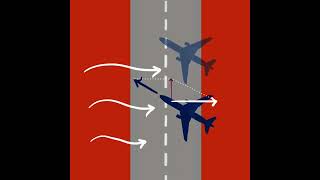
What is Resolution of a Velocity Vector?
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Resolution of a velocity vector refers to the process of breaking a single velocity vector into two components, typically along perpendicular axes, such as horizontal and vertical directions. This is particularly useful in problems involving projectile motion or motion on inclined planes.
Detailed Explanation
The resolution of a velocity vector is an essential concept in physics that involves splitting a single vector (in this case, velocity) into two separate components. These components are typically aligned along the x-axis (horizontal) and the y-axis (vertical). This process provides a clearer understanding of how an object moves in different directions. It is especially useful in scenarios like projectile motion, where the forces acting on an object can be easier to analyze when separated into their vertical and horizontal influences.
Examples & Analogies
Imagine throwing a basketball toward the hoop. The path it takes can be thought of as having both a vertical component (how high it goes) and a horizontal component (how far it travels forward). By analyzing these two components separately, you can better predict where the ball will land.
Components of Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
A velocity vector can be broken down into two perpendicular components, typically in the x-direction (horizontal) and the y-direction (vertical):
vx=vcos(ΞΈ) and vy=vsin(ΞΈ)
Where:
- v is the magnitude of the velocity.
- ΞΈ is the angle the velocity vector makes with the horizontal axis.
- vx is the horizontal component (velocity in the x-direction).
- vy is the vertical component (velocity in the y-direction).
Detailed Explanation
The resolution of a velocity vector is mathematically expressed using trigonometric functions. The formula states that:
v_x = v imes ext{cos}(ΞΈ)
and
v_y = v imes ext{sin}(ΞΈ).
Here, 'v' represents the overall speed of the object, and 'ΞΈ' is the angle the vector makes with the horizontal direction. The horizontal component (vx) represents how fast the object moves in the horizontal direction, while the vertical component (vy) represents how fast it moves vertically. These components are crucial in understanding the complete motion of an object.
Examples & Analogies
Consider a kite flying in the sky. The kite moves through the air, and the angle of the string affects how high it goes (vertical component) versus how far it moves horizontally (horizontal component). By breaking this movement down into its vertical and horizontal parts, you can better understand how to control the kite or predict its path.
Example: Resolution of Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Suppose an object moves with a velocity of 40 m/s at an angle of 30Β° above the horizontal. To find the components:
vx=40cos(30Β°)=40Γβ3/2β34.64 m/s
v_y=40sin(30Β°)=40Γ1/2=20 m/s
So, the horizontal component of velocity is approximately 34.64 m/s, and the vertical component is 20 m/s.
Detailed Explanation
In this example, we start with an overall velocity of 40 m/s at an angle of 30Β°. To resolve this velocity, we use the cosine and sine functions to calculate the horizontal and vertical components. For the horizontal component (vx), we calculate:
v_x = 40 imes ext{cos}(30^ ext{Β°}) ext{which gives approximately } 34.64 m/s.
For the vertical component (vy), we calculate:
v_y = 40 imes ext{sin}(30^ ext{Β°}) ext{which gives } 20 m/s.
These results indicate how much of the object's speed is directed horizontally versus vertically.
Examples & Analogies
Imagine a sprinter running up an incline. Though they may be running at a speed of 40 m/s, breaking that speed into how much is going up the hill and how much is moving forward on the flat can greatly affect their performance. The horizontal speed helps them cover ground, while the vertical speed helps them conquer the incline.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Resolution of Velocity: The breakdown of a velocity vector into its horizontal and vertical components for easier analysis.
-
Vector Components: Understanding how to calculate the x and y components of a velocity vector using trigonometric functions.
-
Applications: The importance of resolving velocity in practical scenarios such as projectile motion and inclined planes.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
An object moves with a velocity of 40 m/s at 30Β° above the horizontal, resulting in horizontal and vertical components of approximately 34.64 m/s and 20 m/s respectively.
-
A plane flying at 200 m/s at 40Β° will have a horizontal component of approximately 153.2 m/s and a vertical component of approximately 128.6 m/s.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Break down the vector, in two we divide, \n X goes left, Y goes up high with pride!
π Fascinating Stories
-
Imagine a bird soaring at a diagonal. It needs to know how much it can move left and how much up. By resolving its velocity, it can decide how to dodge the wind.
π§ Other Memory Gems
-
C-oz, S-in: \(V_x = V\cos(\theta),\ V_y = V\sin(\theta)\) - remember how to calculate components!
π― Super Acronyms
VIVE
- Velocity In Vector Evaluation β remember to always evaluate your velocities using their components.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Velocity Vector
Definition:
A vector quantity that includes both the speed and direction of an object's motion.
-
Term: Component
Definition:
A piece of a vector quantity that can represent motion along a specific axis, typically horizontal or vertical.
-
Term: Resolution of Velocity
Definition:
The process of breaking down a single velocity vector into its components along different directions.
-
Term: \(\theta\)
Definition:
The angle formed between the velocity vector and the horizontal axis.