Professional Courses
Industry-relevant training in Business, Technology, and Design to help professionals and graduates upskill for real-world careers.
Categories
Interactive Games
Fun, engaging games to boost memory, math fluency, typing speed, and English skillsβperfect for learners of all ages.
Typing
Memory
Math
English Adventures
Knowledge
Enroll to start learning
Youβve not yet enrolled in this course. Please enroll for free to listen to audio lessons, classroom podcasts and take mock test.
Interactive Audio Lesson
Listen to a student-teacher conversation explaining the topic in a relatable way.
Introduction to Composition of Velocity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Today, we're learning about the composition of velocity. Can anyone tell me what composition means in the context of motion?
Is it when we combine different speeds together?
Exactly! Composition of velocity refers to combining two or more velocities to find a resultant velocity. It's like adding two arrows together that are pointing in different directions.
How do we add them if they're not going the same way?
Great question! We use vector addition. That means we add them based on both their magnitudes and their directions. For example, if one velocity is going north and the other goes east, we can find the resultant using a right triangle.
So, it's like the Pythagorean theorem?
Absolutely! In fact, if two velocities are perpendicular, we use the Pythagorean theorem to calculate the resultant velocity.
Can we see an example of that?
"Sure! For example, if one object moves at 30 m/s east and another at 40 m/s north, the resultant velocity would be found using the equation:
Understanding Resolution of Velocity
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Now that we understand composition, letβs talk about the resolution of velocity. Does anyone know what it means to resolve a velocity?
Is it breaking it down into parts?
Exactly! Resolution of velocity involves breaking down a velocity vector into its components, usually along perpendicular axes, like vertical and horizontal.
Why do we need to do that?
Good question! It simplifies problems involving motion. For example, in projectile motion, the horizontal component remains constant, while the vertical component changes due to gravity.
How do we find those components?
"We can use the formulas:
Applications of Velocity Composition and Resolution
Unlock Audio Lesson
Signup and Enroll to the course for listening the Audio Lesson
Letβs talk about where these concepts are applied in real life. Can anyone think of an example?
Maybe in sports?
Yes! In sports, athletes often need to adjust their velocity based on motion direction, like in basketball or football. Another example is projectile motionβlike a ball being thrownβwhich needs resolution of velocity to analyze its path.
What about inclined planes?
Exactly! When an object moves on an inclined plane, we resolve its velocity into two componentsβone parallel to the incline and one perpendicular to it. This helps us understand the forces acting on the object.
How does this help in real-world physics?
It allows engineers to design better systems, such as roller coasters or vehicles on hills. Understanding these components helps predict motion more accurately.
In summary, the concepts of composition and resolution of velocity are critical in analyzing motion in many practical and theoretical applications.
Introduction & Overview
Read a summary of the section's main ideas. Choose from Basic, Medium, or Detailed.
Quick Overview
Standard
In this section, students learn about the composition of velocity, which combines multiple velocities to find a resultant vector, and the resolution of velocity, which breaks a single velocity into perpendicular components. These concepts are crucial for understanding motion in different contexts, such as projectile motion and inclined planes.
Detailed
Detailed Summary of Composition and Resolution of Velocity
Introduction
The concepts of composition and resolution of velocity are foundational in understanding motion in physics.
Composition of Velocity
- Composition of Velocity: This refers to combining two or more velocities acting in different directions to obtain a resultant velocity. When the velocities are not in the same line or direction, vector addition is used to find this resultant velocity.
Resolution of Velocity
- Resolution of Velocity: This involves breaking down a single velocity vector into its components along different directions, typically horizontal and vertical. This simplification helps in solving problems where the velocity is not aligned with the standard reference frame.
Understanding these concepts allows students to solve real-world problems in physics, such as projectile motion and motion on inclined planes.
Youtube Videos
Audio Book
Dive deep into the subject with an immersive audiobook experience.
What is Composition of Velocity?
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
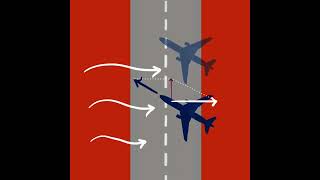
The composition of velocity refers to combining two or more velocities acting on an object in different directions. In this process, the individual velocities are added vectorially to determine the resultant velocity.
Detailed Explanation
Composition of velocity involves the process of adding two or more velocities that are acting on an object. Unlike simple addition where we only consider magnitude, in vector addition, we also take into account the direction of each velocity. This means if two cars are traveling in different directions, we would calculate the resultant velocity by considering both their speeds and the angles at which they are moving. The resultant velocity is what you get when all these different velocities are combined into one single vector.
Examples & Analogies
Imagine you are rowing a boat on a river. If you're rowing upstream at 2 m/s and the current is flowing downstream at 3 m/s, to find out the speed and direction of the boat with respect to the riverbank, you would combine these two velocities. The resultant velocity would tell you how fast youβre effectively moving towards your destination.
Vector Addition for Resultant Velocity
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
In cases where velocities are not acting in the same line or direction, vector addition is used to find the resultant velocity, which is the combined effect of all the individual velocities.
Detailed Explanation
When dealing with velocities that are not aligned in a straight line, vector addition comes into play. This involves creating a vector diagram where each velocity is represented as an arrow, considering both magnitude and direction. By following vector addition methods such as the head-tail method or using trigonometry, you can determine the resultant vector that represents the overall effect of all the individual velocities on that object.
Examples & Analogies
Think of two friends pushing a shopping cart. One friend pushes from the side, while the other pushes from the back. The final direction and speed of the cart depend on both friends' pushes; hence, to find out the resultant effect, you would analyze the angles and the strength of their pushes.
What is Resolution of Velocity?
Unlock Audio Book
Signup and Enroll to the course for listening the Audio Book
Resolution of velocity involves breaking down a single velocity into its components along different directions, usually perpendicular to each other (e.g., horizontal and vertical components). This helps simplify problems in motion when the velocity is not aligned with the axes of the reference frame.
Detailed Explanation
Resolution of velocity is the process of decomposing a single velocity vector into two or more components that are typically perpendicular to each other. This approach is particularly useful in physics to simplify the analysis of motion, especially when using coordinate systems. By breaking down a vector, you can focus on its effects in each direction independently, making calculations easier and more manageable.
Examples & Analogies
Consider a soccer player kicking a ball at an angle. Instead of only looking at how fast the ball is going, we can resolve its velocity into horizontal and vertical components. This helps us predict how far and how high the ball will travel. Imagine you're throwing a ball; separating the motion into horizontal (how far it goes) and vertical (how high it goes) helps you understand its path.
Definitions & Key Concepts
Learn essential terms and foundational ideas that form the basis of the topic.
Key Concepts
-
Composition of Velocity: Refers to combining two or more velocities to find the resultant vector.
-
Resolution of Velocity: The process of breaking a velocity vector into its perpendicular components.
-
Resultant Velocity: The total velocity obtained when adding individual velocity vectors using vector addition.
-
Pythagorean Theorem: A mathematical principle used to calculate the resultant of two perpendicular vectors.
-
Components of Velocity: Individual parts along standard reference axes used to analyze motion.
Examples & Real-Life Applications
See how the concepts apply in real-world scenarios to understand their practical implications.
Examples
-
A car traveling at 60 m/s northeast and another at 30 m/s southeast. The resultant velocity can be calculated using vector addition.
-
An object thrown at 45Β° with a velocity of 20 m/s; its components can be resolved using trigonometric functions.
Memory Aids
Use mnemonics, acronyms, or visual cues to help remember key information more easily.
π΅ Rhymes Time
-
Add your velocity, angle and speed, together they go, that's the motion's need.
π Fascinating Stories
-
Once there was a clever archer who could shoot arrows in two directions. He knew that to strike the target, he had to combine his aim and pull into one direction, showing how he'd use vector composition to combine forces.
π§ Other Memory Gems
-
RAC: Resultant, Add, Combine to remember composition of velocity.
π― Super Acronyms
VCR
- Velocity Composition Resolution for understanding the two main concepts.
Flash Cards
Review key concepts with flashcards.
Glossary of Terms
Review the Definitions for terms.
-
Term: Composition of Velocity
Definition:
The process of combining two or more velocities acting on an object in different directions to obtain a resultant velocity.
-
Term: Resolution of Velocity
Definition:
The process of breaking down a single velocity vector into its components along different directions, usually perpendicular.
-
Term: Resultant Velocity
Definition:
The total velocity resulting from the vector addition of multiple individual velocities.
-
Term: Vector Addition
Definition:
The method of combining vectors by adding their magnitudes and directions to produce a resultant vector.
-
Term: Components of Velocity
Definition:
The individual parts of a velocity vector, usually represented along perpendicular axes (horizontal and vertical).